Міністерство освіти і науки України
Дніпропетровський національний університет імені Олеся Гончара
Механіко-математичний факультет
Кафедра математичного аналізу і теорії функцій
Дипломна робота першого (бакалаврського) рівня вищої освіти
АНАЛОГИ ТЕОРЕМИ ПОРІВНЯННЯ КОЛМОГОРОВА
ТА ЇХ ЗАСТОСУВАННЯ
Допускається до захисту:
т. в. о. завідувача кафедри, ____________ (В.П. Моторний)
д. ф.-м. наук
Рецензент: ____________ (О.О. Пипка)
доцент кафедри МГА,
к. ф.-м. наук
Керівник: ____________ (О.В. Коваленко)
доцент кафедри ММА,
к. ф.-м. наук
Виконавець: ____________ (К.Ю. Конограй)
студентка групи ММ-13-1
Дніпро
2017
РЕФЕРАТ
Дипломна робота освітньо- кваліфікаційного рівня бакалавр :30 с., 13 рис., 10 джерел.
Об’єктом дослідження є ідеальні сплайни Ейлера та їх аналоги.
Мета: отримання аналогів теореми порівняння Колмогорова.
Методи дослідження: класичні методи математичного та функціонального аналізу.
Одержані
теореми порівняння для
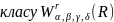є новими.
Результати дослідження можуть бути застосовані при дослідженні екстремальних задач функціонального аналізу та теорії наближення.
Ключові слова: ТЕОРЕМА ПОРІВНЯННЯ КОЛМОГОРОВА, СПЛАЙНИ ЕЙЛЕРА, НЕСИМЕТРИЧНІ СПЛАЙНИ.
SUMMARY
The graduation paper consists of 30 pages, 13 pictures, and 10 references.
The object of research is ideal Euler splines and their analogues.
The objective of research is proof of Kolmogorov’s comparison theorem analogues.
Research methods are classic methods of math and functional analysis.
Obtained
comparison
theorems for the class
of
functions
are new.
The results can be used for research of extremal problems of Functional Analysis and Approximation Theory.
Key words: Kolmogorov`s comparison theorem, Euler splines, nonsymmetrical splines.
ЗМІСТ
ВСТУП……………………………………………………………………………......5
Основні позначення………………………………………………………………….6
Розділ 1. Відомі результати…………………………………………………………7
Теорема порівняння, симетричний випадок………………………………...8
1.2 Несиметричний випадок……………………………………………..……..11
1.3 Випадок класу, який задається обмеженнями на декілька похідних……14
Розділ
2. Функція
та її властивості
……………………….………...19
2.1 Означення екстремальної функції…………………………………………19
2.2 Деякі властивості екстремального сплайна……………………………….21
Розділ 3.Основні результати……………………………………………………….22
ВИСНОВКИ…………………………………………………………………….......29
ПЕРЕЛІК ВИКОРИСТАНИХ ДЖЕРЕЛ………………………………………….30
ВСТУП
Теоремами порівняння називають твердження, які дають оцінку тій чи іншій характеристиці функції із деякого класу через відповідну характеристику деякої фіксованої функції. Останню функцію можна вважати еталонною або стандартною для даного класу; її також називають функцією порівняння для даного класу.
Першу
теорему такого типу довів А. М. Колмогоров.
Він показав, що ідеальні ейлерові сплайни
є функціями порівняння для функцій з
класу
.
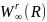Як сам результат, так і метод його доведення зіграли велику роль. Завдяки теоремі порівняння були виведені точні нерівності для норм похідних типу відомої нерівності Колмогорова. Згодом використання ідей, пов’язаних із теоремами порівняння, дало можливість отримати ряд нових точних результатів, які з’ясовують екстремальні властивості функцій.
З огляду на вищевказане, тема роботи актуальна.