Билет №1.
1.1 Сигнал –материальный носитель инфы. Классификация сигналов: 1) По мат.-ому представлению: детерминированные (регулярные, в любой момент t точно известно значение S) и случ. сигналы. Детерминированные сигналы: периодические(S(t) = S(t+nT) и непериодические сигналы. 2) По врем. Представлению: аналоговые((непрерывны), дискретные(совокупность точек), цифровые(двоичный код).
Модуляция
– это изм-е параметра сигнала во t.
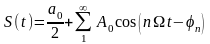тригонометрическая
запись.и ряды фурье.
1.2 Переход м/у обл. полупроводника с электропроводностью
p- и n типа наз-ют электронно-дырочными или p-n переходами. Классификация p-n переходов: Ступенчатыми переходами, Плавными переходами. По соотношению концентраций примесей в p и n слоях переходы: симметричные(p n), несимметричные(p >> n или n << p) и односторонние(резкая асимметрия). Область образовавшихся простран-ных зарядов и есть обл. p – n перехода.Рис.часть электронов диффундирует из слоя nв слой p. При этом в слое p
вблизи границы окажутся избыточные электроны, кот. будут рекомбинировать с дырками до тех пор, пока не будет выполнено
условие равновесия np= n(i) ^2. Соответственно в этой обл. уменьшится концентрация свобод. дырок и "обнажатся" некомпенсированные отр. заряды акцепторных атомов. Слева от металлургической границы "обнажатся" некомпенсированные полож. заряды ионов доноров, поскольку часть элект. перешла отсюда в слой p(рис 7.1б). Аналогичные рассуждения действительны для дырок слоя p, которые частично диффундируют в слой n. Однако в несимметричном переходе, в котором nn >> pp, диффузия дырок в слой
n мало существенна, поскольку разность концентраций p(p)- p(n)
значительно меньше разницы n(n) – n(p), а именно этими разностями опред-тся градиенты концентраций и диффузионные токи. Часто эту обл. наз-ют обедненным слоем.
Для
n(n)
p(p) ширина p-n перехода для равновесного
со- стояния определяется как :
Метал полностью пропускает ток, так как нет зазора. Полупроводник пропускает ток при не нулевой температуре. Так как эл-ам нужно перепрыгнуть из валентной зоны в зону проводимости. Величина зазора не должна быть более 3,5 эВ. Диэлектрик- они как и у полупроводников не перекрываются, и расстояние м/у ними составляет, условно, более 3,5 эВ. Для того, чтобы перевести эл. из валентной зоны в зону проводимости требуется значительная энергия (температура), поэтому диэлектрики ток при невысоких температурах практически не проводят.
Билет №4.
4.1 При гарм. Возд-и на лин. Цепь все токи и напр также имеют форму гарм. Колеб, т.Е. Их комп-х амплитуд.(рис-перемен. Цепь)
О
тн-е
комп-х амплитуд напр. и тока на входе
двухполюсника наз-ся комплекс. вх. сопр.
(сокращенно – комплекс. сопр.м) и
обозначается Zвх.
где
zвх
наз-ся полн. вх. сопр., а угол φ=ψu-
ψi
представляет собой сдвиг фаз между
напр.м и током. Компл.-е сопр., как и
всякое комп. число, может быть представлено
в алгебраической форме:
-
коэф.
при мнимой части комплексного числа
Zвх, наз-мый реактивной составляющей
входного сопротивления. Полное сопр.:
Элементарные цепи переменного тока.Будем называть элементарными цепями переменного тока такие идеализированные цепи, схемы кот. содержат, кроме ист. гарм. колебаний, один из трех эл.: сопр. r, емкость C, или индуктивность L.а. Активное сопр. при гарм. Возд.
П
усть
на сопр. r (рис.2.3) действует напр.,
изменяюще-
еся
во времени по гармоническому закону
u=Ucos(ωt+ψu).К
омп.
амплитуды напр. и тока:
Вх. сопр. цепи –вещественная величина, т.е.Реактивная составляющая сопротивления xвх=0. Следовательно, согласно формуле. φ=ψu-ψi=0, т.е. напр. и ток совпадают по фазе. В сопр. r расходуется энер.. Мгновенная скорость поступления энергии в цепь, т.е. мгн-ая мощность p=(i^2)*r. Подставляя сюда мгн.значение тока i=Icos(ωt+ψ),получим
Ср. знач. расходуемой мощности наз-ют актив. мощностью.
Действующим
знач. переменного тока Iд наз-ся велич.
такого пост. тока, который выделяет в
данном сопр. ту же мощность, какая в нем
расходуется в среднем за T
при прохождении переменного тока.
Сопр.
r участка цепи переменному току называют
актив. сопр.м. б.
Емкость
ψ
i=ψu+π/2.
ток опережает по фазе напр. на угол π/2.
Комп.сопр яв-ся чисто мнимой величиной.
Ч
Х
емк-ого сопр. xC(ω)
и емк-ой проводимости bC(ω)=1/xC(ω).
С
увелич. частоты емкостное сопр. падает,
при выс. частотах оно становится весьма
малым и режим ист. приближается к кор-ому
замык-ю. Наоборот, для постоянного тока
(ω=0) емкостное сопр. бесконечно велико,
т.е. цепь разомкнута. Емкость С яв-ся
энергоемким эл-ом цепи. В элек-ом поле,
сосредоточенном в емкости С , запасается
энергия, мгновенное знач. Кот.
Мгновенная
мощность=
Среднее
значение мощности=
активной (расходуемой) мощности в
излуч-ой цепи нет.
.
Реак.
мощность.
Абс. Знач. реактивной мощ-ти = макс. скорости запасания энергии в эл. Поле.
в. Индуктивность при гармоническом воздействии
ψi=ψu-π/2,
т.е. ток отстает от
напряжения
на угол π/2. Комп. Сопр. Мнимая
Энергия=
ЧХ
мгновенная
мощность
реакт.мощность
Билет 4(продолжение).
Послед.экви.
Ток
через сопротивление Zн
напр.на
нагрузке
Парал.экв.
напр.на
нагруз.
сила
тока на нагруз.
при
I(г)=I(кз)
4.2.Транзистором наз-ют полупроводниковый прибор с одним или неск. Эл-ими переходами, пригодный для усиления мощности эл-ких сигналов. В основе работы биполярных транзисторов лежит инжекция неосновных носителей
.
а)
P-n-p
б) n-p-n
Переход, раб-ий в прям. Направ., наз-ся эмиттерным, а крайний слой – эмиттером. Ср. слой наз-тся базой. Второй переход, нормально смещенный в обр. направ., наз-ся коллекторным, а крайний слой – коллектором.Чтобы «собирание коллектором» было возможным, база должна иметь достаточно малую толщину. Если база однородная, то движ. носителей диффузионное. Если база неодн. то в ней есть внутр. Эл. поле, и тогда двж-ие носителей будет комбинированным: диффузия сочетается с дрейфом. В нормальном активном режиме, на эмиттерный переход подается прям. напр., а на коллекторный – обр. При этом электроны инжектируются из эмиттера в
базу, проходят ее почти без рекомбинации (поскольку ширина базы мала) и беспрепятственно попадают в коллектор. Сопр. Обр. смещенного коллекторного перехода очень велико – несколько МОм. Поэтому в цепь коллектора можно вкл. Бол. Сопр. нагрузки, не изм-яя велич. коллекторного тока. Сопротивление прямо смещенного эмиттерного перехода мало. Поэтому при почти
одинаковых токах мощность, потребляемая в цепи эмиттера, оказ-ся меньше, чем мощность, выделяемая в цепи нагрузки. Следовательно, транзистор способен усил. мощность, т.е. является усил. прибором. режим насыщения или режим двойной инжекции. на обоих переходах – эм и кол – действуют прям. напряжения. Эм и
кол инжектируют носители в базу навстречу друг другу и одновременно каждый из них собирает носители, дошедшие от др.слоя. Если оба перехода смещены в обр. направ., то ч\з транзистор будет протекать мин. тепловой ток. Такой режим наз-ся режимом отсечки
схемы
включения(ОБ,ОЭ,ОК)
ОБ:
α-коэф.
передачи
тока эм. в цепь кол. Эта
схема не обеспечивает ус. по току и
обладает мал. Вх сопр.
ОЭ:
β
– коэф. передачи тока базы в цепь кол.
и составляет десятки единиц, причем,
незначительные изменения α приводит
к большим изменениям β. Ток i(k0)*
- обратный ток коллектора для схемы с
ОЭ. Недостатки
данной схемы – худшие частотные и
температурные свойства по сравнению
с ОБ.
ОК: Вх.сопр. составляет десятки килом, что яв-ся важным достоинством схемы.
Билет №7.
7.1 ОЭ.
β
– коэф. передачи тока базы в цепь кол.
и составляет десятки единиц, причем,
незначительные изменения α приводит
к большим изменениям β. Ток i(k0)*
- обратный ток коллектора для схемы с
ОЭ. Недостатки
данной схемы – худшие частотные и
температурные свойства по сравнению
с ОБ. Коэф. ус. по току, по напр. и по мощ.
(десятки-сотни), Rвх(сотни
Ом-единицы кОм), Rвых(единицы-десятки
кОм), фазовый сдвиг 180град.
Вх(рисб)
и вых.(рисА) хар-ки. Для
ОБ:
по
рис.Б
При uкб=0 хар-ка идет из начала коор., так как ток = 0. А если uкб>0, то характеристика проходит выше, т.е. возникает
ток эм., и при uэб=0 протекает небольшой начальный ток iэн.. Условие uзб=0 соответствует короткому замыканию эмиттера и базы. Хар-ки
д
ля
различ. uкб расположены оч. Близко, т.к
Мал. влияние напр. uкб на ток эм. объясняется
тем, что поле, создаваемое напр. uкб,
сосредоточено в кол. переходе. По
рис А:
Они
даются для постоянных значениях тока
эмиттера i(э). При iэ=0 хар-ка проходит
через начало координат. Раб. участки
вых. Хар-ик для различ. Iэ представляют
собой прям. линии, идущие с небольшим
наклоном, что означает малое влияние
напр. u кб на ток кол.Для
ОЭ: Рис А
Кривые коллекторного семейства не пересекают ось ординат и пол-
н
остью
расположены в Iквадранте. Это легко
понять из соотношения Uкэ= Uкб + Uбэ,
кривые ОЭ получаются путем сдвига
кривых ОБ на велич.U
бэ.
Кривые
кол. семейства менее регулярны, чем в
схеме ОБ: они имеют гораздо бол., неодин-ый
наклон и заметно сгущаются при бол.
токах. Ток при оборванной базе (когда
Jб = 0) намного больше тока Jк0 при оборванном
эм. и зависит от вых. напр. Вх. ток базы
J бможет иметь не только положительную,
но небол. Отр. величину (т.е. для n - p – n
транзистора вытекать из базы).РисБ:
Кривые
баз-о семейства по срав. с эм. Сем. не
только имеют другой масштаб тока, но
сдвинуты вниз на велич. Тока Jк0, кот.
протекает в базе тогда, когда ток Jэ= 0.
Кроме того, кривые несколько более
линейны, чем при вкл. ОБ. Все
параметры можно разделить на собственные
(или первичные) и вторичные.
Стат. Парам. Тран. для тран. С ОБ.Т.к
дей-ют мал. Перемен. Сост-ие, то пост. и
перемен.сот-ие анализ. и рассчит.
раздельно. 1)
Дифф-ый коэф. передачи эм. тока в цепь
кол.:
2)Диф. Сопр. Эм. перехода, вкл.в прям. Напр.:
3
)сопр.кол.(обр.
напр)
4
)
Объемное
сопротивление базы (rб),rб-(попер.
объемное сопр. базы – сопр. Баз. току)
5)крутизна(S)
6) Ко
эф.Внут.Обр.связи
по напр.: Парам с ОЭ:
r
э
и rк
имеют тот же физ. смысл, что и в схеме
ОБ, а сопротивление коллекторного
перехода r*,
β-диф.передачи баз. тока в цепь кол.