Предикатное уравнение для усеченного конуса:

,

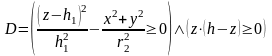где .

Программа вычисления значения r-функции для усеченного конуса:

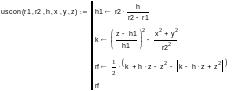
Примеры

uskon(7,10,10,5,7,5) = -0.017 uscon(7,10,10,5,4,5) = 0.38 uscon(7,10,10,5,12,5) = -0.968

2.6 Параллелепипед

Плоскости граней параллелепипеда параллельны координатным плоскостям ССК. Одна из вершин параллелепипеда совпадает с началом координат. Параллелепипед задается 3 параметрами – длинами ребер a, b, c (рис.7).

Рис. 7

Предикатное уравнение для параллелепипеда:

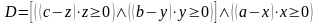
Программа вычисления значения R-функции:

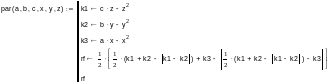Внимание

В данной программе не производятся последовательные пересечения R-функций областей пространства. В четвертой строке записано выражение, в котором производятся сразу две операции пересечения.

Примеры

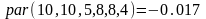
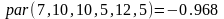
Второй способ – начало координат в центре параллелепипеда.

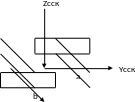
Xсск

Рис.8

Предикатное уравнение

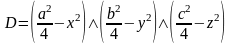
Программа вычисления значения R-функции

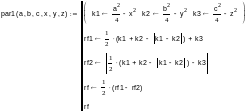
Примеры

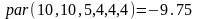
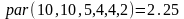
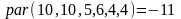
2.7 Полупространство

Полупространство определяется одним параметром – расстоянием h между плоскостью xy ССК и ограничивающей полупространство плоскостью (рис.9).

Рис.9

Предикатное уравнение:

.

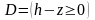Программа вычисления значения R-функции:

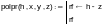
Примеры

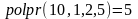
2.8 Тор

Тор задан двумя параметрами (рис.): – радиус осевой линии тора, – радиус круга – сечения тора.

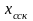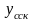Через точки О и А проведем плоскость перпендикулярную плоскости О . Плоскость пересекает осевую линию в точке В.

В качестве значения R-функции в точке A(x,y,z) принимается величина .

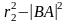Блок-схема алгоритма вычисления значения R-функции для тора приведена на рис.11.

Программа вычисления значения R-функции:

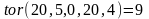
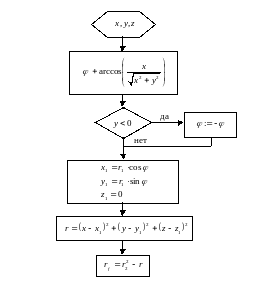
Рис.11

2.9 Труба

Труба задана тремя параметрами (рис.): – внутренний радиус, – наружный радиус, h – высота трубы.

Рис. 12

Предикатное уравнение:

.

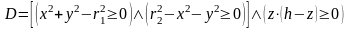Программа вычисления значения R-функции трубы в точке (x,y,z) запишется так:

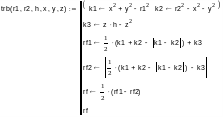
Примеры:

trb( 10,15,20,0,13,10) = 56 trb( 10,15,20,0,17,10) = -64

trb( 10,15,20,0,5,10) = -75 trb( 10,15,20,0,13,25) = -125

2.10 Бак

Бак задан четырьмя параметрами (рис.): – радиус цилиндрической обечайки, – радиус нижнего днища, 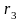– радиус верхнего днища, h – высота цилиндрической обечайки. На параметры накладываются ограничения: , .

Рис.13

R-функция бака формируется как R-функция объединения цилиндра и двух шаровых сегментов.

Предикатное уравнение цилиндра:

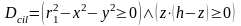
Предикатное уравнение сегмента нижнего основания:

,

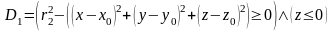где (x,y,z) – координаты точки, в которой вычисляется значение R-функции;

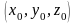- координаты центра шара, из которого вырезается нижний сегмент.

Так как 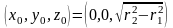, то

Предикатное уравнение сегмента верхнего основания:

,

где 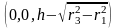– координаты центра шара, из которого вырезан верхний сегмент.

Окончательно, предикатное уравнение для бака запишется в виде:

Программа вычисления значения R-функции бака в точке (x,y,z) запишется так:

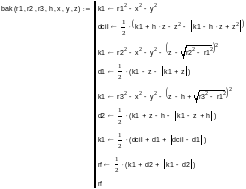
Примеры