
- •1 Введение
- •2 Примеры составления r-функций
- •- Точка находится внутри шара;
- •2.2 Бесконечный полуцилиндр
- •2.4 Конус
- •2.5 Усеченный конус
- •Предикатное уравнение для усеченного конуса:
- •Программа вычисления значения r-функции для усеченного конуса:
- •2.6 Параллелепипед
- •2.7 Полупространство
- •2.9 Труба
- •2.11 Референц – эллипсоид поверхности Земли
- •2.12 Программа вычисления расстояния до поверхности референц – эллипсоида из точки, заданной своими координатами в иск, по направлению луча, определяемому ортом e. Координаты орта задаются также в иск
- •3 Задание для выполнения
- •4 Алгоритм выполнения задания
- •5 Выводы:
Лабораторная работа №1
Элементы твердотельного моделирования на Mathcad. Базовые элементы форм. Алгоритмы и программы вычисления значений R-функции для базовых элементов форм и их композиций
1 Введение
Компьютерный век породил теорию R-функций — функций с «логическим зарядом», возникшую на стыке дискретного и непрерывного анализов, использующую аппарат булевой алгебры, который органически присущ и ЭВМ. На основе теории R-функций была решена обратная задача аналитической геометрии, появилась возможность строить в виде элементарной функции уравнение границы сложного объекта, и притом такое уравнение, которое обладало бы необходимыми дифференциальными свойствами. В. Л. Рвачев с помощью конструктивного аппарата теории R-функций разработал единый подход к проблеме построения координатных последовательностей для основных вариационных и проекционных методов. К настоящему времени метод R-функций был применен для решения большого числа задач электродинамики, механики деформируемого твердого тела, теории пластин и оболочек, гидродинамики и магнитной гидродинамики, теплофизики и др.
Рассмотрим один из подходов к решению задач твердотельного моделирования конструкций, основанный на применении базовых элементов форм (БЭФ) и программ вычисления R-функций для БЭФ и конструкции в целом. В простейшем случае трехмерный образ поверхности конструкции (КА, РН) может синтезироваться из БЭФ с помощью логических операций «И», «ИЛИ», «НЕ». Информация о способе объединения БЭФ в единую конструкцию (компоновку) содержится в R-функции конструкции. Программа вычисления R-функции конструкции является, в сущности, математическим описанием объемной модели конструкции.
Основное свойство R-функции для выделенной области пространства состоит в том, что внутри области она положительна, на границе равна нулю, вне области – отрицательна. R-функции всюду непрерывны. Вследствие того, что R-функции несут в себе больше информации, чем обычные булевские функции, использование R-функций гораздо предпочтительнее. Это объясняется тем, что по модулю значения R-функции для точки можно судить о расстоянии этой точки до поверхности тела.
Пусть
заданы две области тела А и В пространства
с определенными на них R-функциями
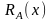 и
и
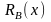 .
Значения R-функций
для областей пространства, полученных
в результате выполнения операций
объединения (1.1), пересечения (1.2), отрицания
(1.3), могут быть вычислены с помощью
соотношений :
.
Значения R-функций
для областей пространства, полученных
в результате выполнения операций
объединения (1.1), пересечения (1.2), отрицания
(1.3), могут быть вычислены с помощью
соотношений :
 (1.1)
(1.1)
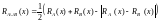 (1.2)
(1.2)
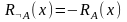 (1.3)
(1.3)
Рассмотрим базовые элементы форм и программы вычисления R-функций для них.

2 Примеры составления r-функций
2.1 Шар
Шар задается одним параметром – радиусом шара (r). Начало ССК шара совпадает с его центром (рис. 1).

Рис.1
Уравнение шара имеет вид:
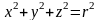 ,
,
где r – радиус шара.
Так как нас интересует та часть пространства, которая расположена внутри шара, то R-функция внутри шара должна быть больше нуля. Тогда предикатное уравнение будет иметь вид:

Программа вычисления значения R-функции для шара в точке (x,y,z) запишется так:
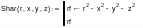
Проверка работы R-функции:
- Точка находится внутри шара;
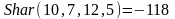 -
точка находится снаружи шара.
-
точка находится снаружи шара.
