1. Первый закон термодинамики в общем виде, определение количеств воздействия данного рода, запись первого закона термодинамики для термомеханической системы (вывод).

2. Энтальпия, ее физический смысл, первый закон термодинамики в записи через энтальпию.

3. Теплоемкости газов. Теплоемкости с_р и с_v. Определение теплоемкости произвольного процесса (вывод). Экспериментальные методы определения теплоемкостей.

4. Энтропия как величина, характеризующая особенности теплообмена между системой и средой. Формулы для расчета энтропии (вывод).

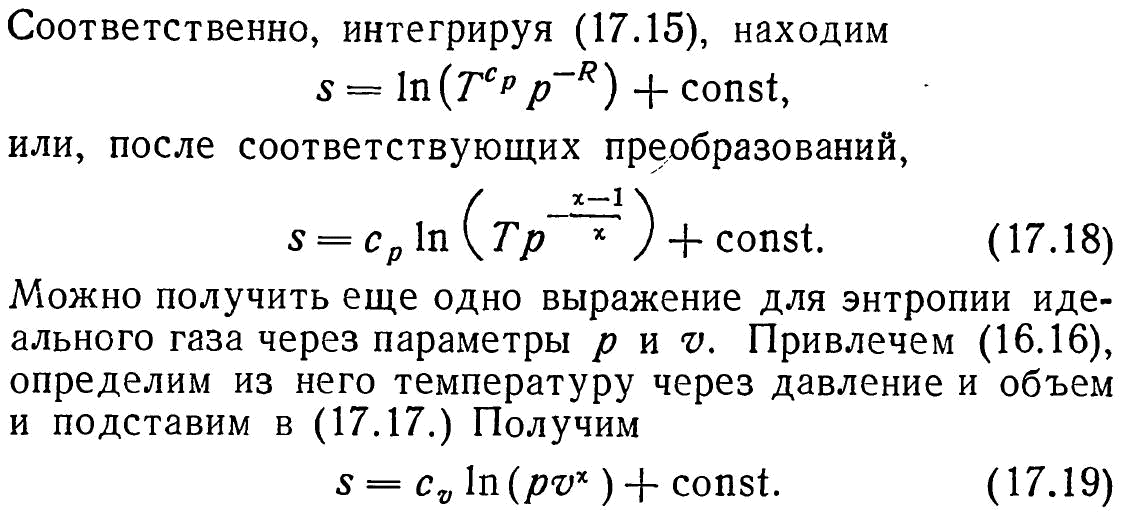
5. Равновесные и неравновесные процессы, их особенности и значение для практики. Принцип возрастания энтропии (второй закон термодинамики).

6. Политропные процессы, связи между параметрами, расчет теплоты и работы за процесс (вывод).

7. Диаграмма h-s воды и пара, принцип ее построения, определение параметров состояния с ее помощью

8. Первый закон термодинамики для потока газа в тепловой и механической формах (вывод).

9. Формулы для расчета скорости и расхода при течении идеального газа или водяного пара (вывод).

10. Связь между скоростью газа и скоростью звука, критические параметры потока (вывод).

11.Влияние формы канала на скорость истечения газа (вывод).

12.Дифференциальный и интегральный дроссель-эффекты (вывод).

13.Газовые смеси, способы описания и расчет их характеристик. Два способа получения смесей, расчет параметров смеси по известным параметрам исходных компонент.

14.Влажный воздух: его основные характеристики, h–d диаграмма влажного воздуха и работа с ней.

15.Расчет основных процессов с влажным воздухом (нагревание, охлаждение, осушка воздуха, работа сушильных камер).

16.Общие понятия о циклах. Особенности организации циклов холодильных машин и тепловых насосов. Понятие о холодильном и теплонасосном коэффициентах, их физический смысл.

17.Цикл и теорема Карно, термический КПД и холодильный коэффициент цикла Карно. Второй закон термодинамики применительно к теории циклов (вывод).

Цикл Карно – это теоретически наиболее эффективный термодинамический цикл. Естественно, что он должен состоять из самых эффективных, с точки зрения получения работы, процессов. Самым эко-номичным в этом плане является адиабатический процесс – в нем работу получаем за счет внутренней энергии, не подводя совершенно тепла извне. Однако из одних адиабат цикл создать невозможно, по-скольку необходимы процессы с подводом и отводом тепла. Из процессов с теплообменом самым при-влекательным является изотермический процесс, в нем все подводимое тепло трансформируется в рабо-ту (если газ идеальный).

Цикл Карно состоит из двух изотерм и двух адиабат. Подвод и отвод тепла здесь осуществляется изотермически, а адиабаты служат для того, чтобы замкнуть цикл (см. рис. телефон). Из рисунка видно, что это единственный цикл, который можно осуществить обратимым способом, подбирая Ти и Тп так, чтобы они отличались от Т1 и Т2, соответственно, на бесконечно малые величины.

Осуществить физически цикл Карно очень трудно, практически невозможно, поскольку это требует так соразмерить темп подвода тепла и темп расширения системы, чтобы увеличение температуры, вы-званное подводом тепла, компенсировалось бы ее уменьшением при расширении. Те же затруднения с изотермическим отводом тепла. Кроме того, дважды за цикл систему необходимо теплоизолировать и дважды снимать эту изоляцию.

Если цикл Карно направить против часовой стрелки, то получим наиболее эффективный холодильный цикл. Его называют обратным циклом Карно.

Найдем теперь кпд цикла Карно:

ηtk=1- q2/ q1 =1- T₂∆s₂/ T₁∆s₁=1-Т2/Т1 (тк S1=S2 и Т2 не равно 0 и Т1 не равно бесконечности) КПД цикла Карно зависит только от температуры и не зависит от рода рабочего тела.

Этот вывод, который непосредственно следует из полученной формулы, составляет первую часть теоремы Карно.

Во второй части этой теоремы утверждается, что КПД цикла Карно является наибольшим для любых циклов, протекающих в заданном температурном интервале Ти … Тп. Чтобы убедиться в этом, сопоставим на Т–s координатах некоторый произвольный цикл и цикл Карно. Заметим, что q1k > q1 на величину заштрихованной влево площади FA1B2CBA, а q2k< q2 на величину площадок, заштрихованных в противоположном направлении FA4D3CDA. С учетом этого сопоставление формул для КПД: ηtk=1- q2k/ q1k и ηt=1- q2/ q1 следует, что ηtk > ηt .

Отношение площади реального цикла к площади цикла Карно на Т–s диаграмме называют коэффициентом заполнения цикла, и по его величине судят о степени совершенства реального цикла.

Второй закон термодинамики применительно к теории циклов.

1. Вечный двигатель второго рода при невозможен (под вечным двигателем второго рода понимается машина, которая могла бы превращать всю подводимую к ней теплоту в работу. Такая машина имела бы КПД = 1).

2. Стопроцентное превращение теплоты в работу посредством тепловой машины - двигателя невозможно. Отношение площади реального цикла к площади цикла Карно на Т–s диаграмме называют коэффициентом заполнения цикла, и по его величине судят о степени совершенства реального цикла. Это сопоставление позволяют дать ещё одну формулировку 2 закона термодинамики: Термический КПД любого реального цикла не может достигать величины 1,0. Обычно это называют невозможностью осуществления вечного двигателя второго рода. Действительно, даже у цикла Карно термический КПД меньше 1,0, поскольку величина Т2 не может быть равно нулю, а величина Т1 – бесконечно большой. По теореме Карно ηtk > ηt значит для любого

цикла, даже не учитывая потерь работоспособности от необратимости, будем иметь ηt < 1,0 .

18.Потери работоспособности, коэффициент качества тепла (вывод).

Максимальная работа, которую может совершить система при обратимых процессах, определяется уменьшением энергии рабочего тела

dlmax = −de = −d (h – T₀s) .

Интегрирование этого выражения для процесса, в котором параметры рабочего тела изменяются от p1, v1, T1 (состояние 1) до p2, v2, T2 (состояние 2) дает

lmax = (h1 − h2 ) + T0 ( s2 − s1 ) = (h1 − h2 ) − T0 ( s1 − s2 ) .

Из формулы видно, что lmax определяется только состояниями рабочего тела и не зависит от характера тех процессов, которыми система перейдет из состояния 1 в состояние 2.

При необратимых процессах изменение энтропии включает в себя дополнительно положительную величину ∆s, которая возникает в результате преодоления внутреннего сопротивления системы. Значит наибольшая полезная работа, которую может отдать система при совершении необратимого процесса, переходя из состояния 1 в состояние 2, будет

l = (h1 − h2 ) − T0 ( s1 − s2 + ∆s_н ) ,

где ( s1 − s2 + ∆s_н ) – полное изменение энтропии в необратимом процессе.

Потеря работоспособности в результате необратимости определится разностью ∆l = lmax − l

Подставляя значения lmax и l, получаем

∆l = (h1 − h2 ) − T0 ( s1 − s2 ) − (h1 − h2 ) + T0 ( s1 − s2 + ∆sн ) = T₀∆sн .

Величина ∆sн тем больше, чем выше степень необратимости процесса, определяемая величиной разности потенциалов.

Для необратимых процессов расширения или сжатия без внешнего теплообмена величину ∆sнм определяют через работу трения lтр, которая практически вся трансформируется в тепло трения qтр, достаточно

просто измеряемое опытным путем, ∆sнм = q тр /Tcр ,

• процессах теплообмена без механических взаимодействий величину ∆sнт определим следующим образом. Максимальную работу тепла q, передаваемого при температуре T1 можно получить, если совершить цикл Карно

• температурном интервале от Т1 до Т0. Величина этой работы:

lmax1 = qηt = q (1 − T0 / T1 ) . (1)

Аналогично найдем максимальную работу того же количества тепла при температуре T2:

lmax 2 = q ηt = q (1 − T0 / T2 ) .

(2)

Потери работоспособности в результате совершения неравновесного процесса, в котором температура изменилась от Т1 до Т2, будет

∆l = lmax1 − lmax 2 = q (1 − T0 / T1 − 1 + T0 / T2 ) = q (T0 / T2 − T0 / T1 ) .

С другой стороны, ∆l = T0 ∆sнт . Приравнивая, получаем:

∆s_нт = q (1 / T2 − 1 / T1 ) .

Из формулы видно, что величина sнт тем больше, чем больше отличаются друг от друга значения Т1 и Т2. При совершении сложных процессов, сопровождающихся и изменениями объема, и теплообменом величину ∆sн находят суммированием

∆s_н = ∆s_нм + ∆s_нт .

Обращая внимание на формулы (1) и (2), можно сделать вывод о том, ценность тепла зависит только от температуры, при которой оно подводится или отводится, и чем ближе эта температура к температуре Т0, тем меньшую долю тепла можно преобразовать в работу. При T = T0 тепловая энергия совсем не обладает запасом работоспособности, т.е. полностью деградирует.

Величину (1 – Т0/Т), которая показывает, какая доля тепла при температуре Т может быть трансформирована в работу в реальных условиях, называют коэффициентом качества теплоты. Анализ, в ко-

тором учитывается качество теплоты и потери работоспособности, называют эксергетическим анализом. Результаты такого анализа всегда являются более точными и информативными, чем при обычном энергетическом анализе. Для примера определим эксергетический коэффициент эффективности холодильных машин:

• ех= q1/Lц(1 – Т0/Т1)= ε*(1 – Т0/Т1)

Поскольку Т1 и Т0 различаются незначительно, то abs (1−T0 /T1) <<1 и поэтому величина εex всегда

меньше

1,0. Когда же мы не учитывали качества теплоты, то получали трудно воспринимаемый результат ε >1.

19.Термодинамические циклы идеальных компрессоров. Влияние промежуточного охлаждения между ступенями на эффективность работы компрессора.

Устройства, предназначенные для сжатия газов, называют компрессорами. Компрессоры бывают поршневыми и осевыми.

Одноступенчатый компрессор представляет собой цилиндр 3 с поршнем 4, перемещаемым с помощью кривошипно-шатунного механизма 5 (см. рис. телефон) В крышке цилиндра устанавливаются автоматические впускной 1 и выпускной 2 клапаны. При движении поршня от верхней мертвой точки вниз в цилиндре возникает разряжение, открывается впускной клапан и происходит всасывание очередной порции газа с давлением р1 в цилиндр. Как только направление движения поршня меняется на противоположное, впускной клапан закрывается и начинается сжатие газа. Когда давление газа в цилиндре достигнет определенной величины р2, открывается выпускной клапан, и сжатый газ выталкивается потребителю.

На рис. (телефон) приведена индикаторная диаграмма идеального компрессора, способного (в отличие от реального случая) вытолкнуть весь сжатый в цилиндре газ. Здесь линия 1–2 изображает процесс сжатия газа в цилиндре, линия 2–3 – выталкивание сжатого газа, а линия 4–1 – всасывание газа в цилиндр. Отметим, что во время всасывания и выталкивания состояния газа не меняются (параметры р и Т газа остаются неизменными), меняется лишь масса газа в цилиндре, т.е. происходит перемещение газа без изменения его внутренней энергии.

Работа на компрегирование одного килограмма газа lк определяется заштрихованной площадью индикаторной диаграммы. При адиабатном сжатии (линия 1–2ад) площадь диаграммы (а значит и работа lк) наибольшая. При изотермическом сжатии (линия 1–2из), наоборот, работа компрессора минимальна. Такое сжатие энергетически наиболее выгодно. Поэтому цилиндр компрессора всегда интенсивно охлаждают или потоком воздуха, или устраивая охлаждающую водяную рубашку. Однако добиться изотермичности сжатия не

удается, и в реальных компрессорах сжатие происходит по политропе с показателем n, причем 1< n < k (k – показатель адиабаты).

Величину lк определим как сумму соответствующих работ

lк = l1-2 + l2-3 + l4-1,

где составляющие рассчитываются по известным формулам:

l_1-2=1/n-1(p₁V₁-p₂V₂);

l_2-3=p₂(V₃-V₂);

l_4-1=p₁V₁;

Тогда в результате суммирования получаем, lк = n/n-1(p₁V₁-p₂V₂);

Мы показали, что работа на привод компрессора в n раз больше работы сжатия.

Абсолютное значение этой работы (на компрегирование) называют работой на привод компрессора lпр, lпр = – lк.

Одной из основных характеристик компрессора является степень повышения давления в нем β = р2 /р1. Обычно 2 ≤ β ≤ 6. При β < 2 применяют вентиляторы и воздуходувки, а при β > 6 возникают пробле-

мы с обеспечением прочности деталей компрессора, кроме того повышенные температуры в конце сжа-тия приводят к закоксовыванию смазки и ускоренному износу.

Если массовая производительность компрессора М кг/с, то теоретическая мощность на привод компрессора будет

Nпр = М lпр .

Для получения высокого давления применяют многоступенчатое сжатие, направляя сжатый в первой ступени газ во второй цилиндр (вторую ступень), третью ступень и т.д. (см. рис.). Обычно газ, сжатый в очередной ступени, направляется сначала в промежуточный холодильник, где его охлаждают до первоначальной температуры, и только после этого он засасывается в цилиндр следующей ступени. Отметим, что благодаря промежуточному охлаждению температура в точках начала процессов сжатия в каждой ступени одинакова (точки 1, 3, 5).

Обычно одинаковыми принимаются и величины β в каждой ступени, поскольку это и есть оптимальное соотношение. При этом число ступеней Z рассчитывают, используя формулу

β=Z* корень р в_ых/р_вх

Для оценки степени совершенства компрессоров используют изотермический КПД

η_из=l_из/l_пр,

где lиз – работа на привод компрессора при изотермическом сжатии в цилиндре; lпр – работа на привод компрессора при политропном сжатии. Понятно, что всегда ηиз < 1,0, и чем выше эта характеристика, тем эффективней компрессор.

Расчет количества тепла, отведенного в цилиндре и холодильнике проводится по известным формулам:

q_цил=с_vm*(n-k)/(n-1)*(Tвых-Tвх) и q_охл= c_pm=(Tвых-Tвх)

работу находят умножением работы на привод одной ступени lпрI на число ступеней Z: lпр = lпрI Z.