10. Средние величины. Способы вычисления значения средней арифметической и средней геометрической

В качестве обобщающего, наиболее типичного для данной совокупности значения признака используется средняя величина.

В зависимости от природы признака, образующего совокупность, выбирается соответствующий вид средней величины.

Для характеристики биологических признаков используются: ср арифметическая, ср квадратическая, ср кубическая, ср гармоническая, ср геометрическая.

Ср арифметическая – частное от деления суммы всех вариант совокупности на объем совокупности =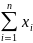 /n – простая ср арифметичекая.

Если в совокупности некоторые варианты повторяются, то среднюю арифметическую можно вычислить по формуле = /n – взвешенная средняя

Где p – частота встречаемости варианты х

Если несколько групп, т.е. несколько однородных совокупностей суммарная средняя:

= /

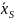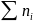
Где ni – объем отдельной совокупности.

Способ условной средней – когда наиболее часто встреч варианту приним за среднюю А и вычисляем = A+ ; xi-A – отклонение каждой варианты от условной средней, n-число измерений.

Если совокупность представлена в форме вариационного ряда с классовым интервалом i, то ср арифметическая:

=A+ /

Где p – частота класса, a – отклонение ср значения класса от условной средней A

Св-ва ср арифметической:

1. =0

2. ; c

с – любая др величина

=min

3. = - ср арифм увелич или уменьш на с

4. Аналогично с умножением и делением

=c = /c

Ср геометрическая – применяется для определения средней относительной скорости изменения какой-то величины во времени. Она характеризует процесс

=

Средняя геометрическая обычно используется при анализе признаков, величины которых во времени меняются по закону геометрической прогрессии(рост поголовья стада, рост численности в популяции и т.д)

Если известны начальные и конечные значения , то скорость прироста может вычисляться по формуле Броди:

W= 100%

Обычно величина вычисляется с использованием логарифмов по формуле

=(lg +lg +…+lg )/n

По значению lg в таблице антилогарифмов или на шкале микрокалькулятора находят величину .

11. Общая схема цифровой электронной вычислительной машины (цвм) и работа её основных функциональных блоков.

Машины, в которых используется цифровая форма представления информации, называются цифровыми вычислительными машинами(ЦВМ). Величины в ЦВМ выражаются в виде цифровой последовательности, которая обычно представляет собой комбинацию нулей и единиц, так как большинство вычислительных машин работает в двоичной системе исчисления. ЦВМ обладаютуниверсальностью и высокой точностью вычислений, они получили наибольшее распространение.

В настоящее время применяется больше количество эвм, но однако как правило, все они содержат в 5 наиболее важных устройств(блоков), каждое из которых выполняет свои специф.функции. Совокупность этих функционально связанных между собой блоков образует структуру эвм. Блоки: память, устройство управления, арифметическо-логическое устройство, устройство ввода и вывода.

Память – устройство для хранения информации. Память делится на оперативную и внешнюю. Оперативная представляет собой совокупность ячеек, в каждую из которых можно поместить число либо команду программы. Внешняя память содержит справочные данные, программы, не используемые ЭВМ в данный момент и другую информацию. Внешняя представлена: магнитными лентами, дисками.

Устройство управления – организует весь процесс работы ЭВМ в соответствии с программой, заданной пользователем. Оно расшифровывает каждую команду и подает сигналы устройствам ЭВМ, участвующим в выполнении команды.

Арифметическо-логическое устройство – осуществляет машинные операции (сложение, умножение и др.) над числами, поступающими из оперативной памяти.

Устройство ввода – предназначено для подачи в ЭВМ информации, которая может вводиться непосредственно с клавиатуры электрической пишущей машинки или дисплея.

Устройство вывода – предназначено для отображения результатов работы ЭВМ, которые могут быть представлены в форме отдельных цифровых величин, таблиц, графиков, геометрических фигур.