11. Вращение твёрдого тела вокруг неподвижной оси. Понятие момента инерции точки, тела. Вычисление моментов инерции однородных симметричных тел( стержня, кольца, диска, цилиндра). Теорема Штейнера.
Абсолютно твердое тело – это тело деформацией, которого можно пренебречь. Вращательным называется такое движение, при котором две точки принадлежащие телу остаются все время неподвижными при движении. Прямая проходящая через эти две точки называется осью вращения. При вращении твердого тела вокруг неподвижной оси все его точки описывают окружности, центры которых лежат на оси вращения, а плоскости перпендикулярны к ней. Тело в этом случае обладает одной степенью свободы, поэтому его положение полностью определяется заданием угла поворота из некоторого начального положения.
Момент инерции материальной точки относительно некоторой оси равен произведению ее массы на квадрат расстояния от точки до этой оси.
J=m умножить на R квадрат.
Момент инерции тела есть сумма моментов инерции материальных точек, составляющих это тело.
J=Jц. т. +m умножить на S квадрат
ц. т. - центр тяжести.
Момент инерции тела относительно оси и относительно точки. Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки до оси. Чтобы найти момент инерции тела (с непрерывным распределением вещества) относительно оси, надо мысленно разбить его на такие малые элементы, чтобы каждый из них можно было считать материальной точкой бесконечно малой массыdm = dV. Момент инерции тонкого диска.Пусть тонкий однородный диск массыmс концентрическим отверстием (рис. 3) имеет внутренний и внешний радиусыR1иR2. Мысленно разобьём диск на тонкие кольца радиусаr, толщиныdr. Момент инерции такого кольца относительно осиY.
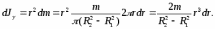
Момент инерции диска: В частности, полагая в (6) R1 = 0, R2 = R,получим формулу для вычисления момента инерции тонкого сплошного однородного диска относительно его оси: Момент инерции диска относительно его оси симметрии не зависит от толщины диска. Поэтому по формулам (6) и (7) можно вычислять моменты инерции соответствующих цилиндров относительно их осей симметрии. Момент инерции тонкого диска относительно его центра также вычисляется по формуле (6), = Jy,а моменты инерции относительно осейXиZравны между собой,Jx = Jz. Поэтому, в соответствии с (3): 2Jx +Jy = 2Jy, Jx = Jy/2
(6)
(7)
(8)
Момент инерции
цилиндра. Пусть имеется полый
симметричный цилиндр массыm, длины h,
внутренний и внешний радиусы которого
равныR1 и R2. Найдём его момент инерции
относительно осиZ, проведенной через
центр масс перпендикулярно оси цилиндра
(рис. 4). Для этого мысленно разобьём его
на диски бесконечно малой толщиныdy.
Один из таких дисков, массойdm = mdy/h,
расположенный на расстоянииyот начала
координат, показан на рис. 4. Его момент
инерции относительно осиZ, в соответствии
с (8) и теоремой Гюйгенса – Штейнера.
рис4
(9)
(10)
Момент инерции цилиндра относительно оси Z(оси вращения маятника) найдём по теореме Гюйгенса – Штейнера
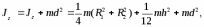
где d– расстояние от центра масс цилиндра до осиZ. В работе 16 этот момент инерции обозначен какJц
Кольца относительно оси, проходящей через его центр и перпендикулярно его плоскости - m*r^2 (m - масса, r - радиус кольца)
Для диска относительно аналогичной оси (m*r^2)/2;
Для стержня через ось, проходящую через него - 0.
Диск относительно диаметра: (m*r^2)/4
Кольцо относительно диаметра: (m*r^2)/2
Стержень относительно оси, перпендикулярной ему и проходящей чере середину: (m*l^2)/12, где l - его длина.
Стержень относительно оси, перпендикулярной ему и проходящей через конец: (m*l^2)/3.
Теоре́ма Гю́йгенса — Ште́йнера (теорема Гюйгенса, теорема Штейнера): момент инерции {\displaystyle J} J тела относительно произвольной неподвижной оси равен сумме момента инерции этого тела {\displaystyle J_{C}} J_{C} относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела {\displaystyle m} m на квадрат расстояния {\displaystyle d} d между осями.