3. 5. Дифракция Фраунгофера на дифракционной решетке. @

Совокупность параллельных щелей одинаковой ширины а, разделенных непрозрачными промежутками шириной b, ле­жащих в одной плоскости, называется одномерной дифракцион­ной решеткой. В зависимости от практического назначения ди­фракционные решетки различаются по виду, материалу и спо­собу изготовления, а также по количеству щелей N (от 0,25 до 6000/мм). Для наблюдения дифракции в видимом свете широко распространены дифракционные решетки, представляющие со­бой прозрачные стеклянные пластинки, на которые алмазным резцом наносятся тонкие параллельные штрихи, являющиеся непрозрачными промежутками шириной b. Сумма d = а + b на­зывается периодом или постоянной дифракционной решетки. Рассмотрим дифракцию плоской монохроматической волны, па­дающей нормально на поверхность решетки периодом d (рис. 3.7). Параллельно решетке расположим собирающую линзу L, а в ее фокадьной плоскости экран Э. Количество щелей в решетке равно N. Любая из щелей при закрытых всех остальных даст на экране спектр, описанный выше. На рис. 3.7 этот спектр обозна­чен пунктирной линиейФазы колебаний в каждой точке любой из N щелей совпадают, так как эти точки принадлежат одной волновой поверхности падающей на решетку пло­ской волны. Следовательно, все щели являются когерентными источниками света и между ними возникает многолучевая ин­терференция. Вид спектра в данном случае усложняется (на рис. 3.7 он представлен сплошной линией). Полученное нами ранее условие дифракционного минимума аsinφ = ±2m λ/2 будет справедливо и в данном случае. В направлениях углов φ, удов­летворяющих этому условию, ни одна из щелей не будет давать свет, поэтому условие аsinφ = ±2m λ/2 является условием глав­ных минимумов для дифракционной решетки. На рис. 3.7 глав­ные минимумы обозначены точками Р₁, Р₁’ и т.д. В центре эк­рана точке О соберутся лучи от всех щелей, идущие под углом φ = 0, т.е. без разности хода. В результате сложения их амплитуд суммарная амплитуда в точке О будет в N раз больше, а интен­сивность в N² раз больше, чем в случае одной щели.

Рассмотрим любую пару соседних щелей, изображенных на рис. 3.7. Разность хода от соответствующих точек обеих ще­лей (например, крайних) Δ = ВС = dsinφ и разность фаз 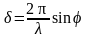. Из условия интерференционного максимума если dsinφ = ±mλ и δ = ±2πm, то колебания от соседних щелей вза­имно усилят друг друга. Следовательно, в направлениях, опре­деляемых углами любая пара щелей даст макси­мум. Поэтому условие dsinφ = ±mλ, где m = 0, 1, 2…есть условие главных максимумов дифракционной решетки. Число m опреде­ляет порядок главного максимума. Количество главных макси­мумов в наблюдаемой дифракционной картине будет зависеть от величин d и λ. Так как модуль sinφ не может быть больше единицы, то максимальное число m ≤ d/λ. Положение главных максимумов не зависит от числа щелей N. Многолучевая интер­ференция между более далеко расположенными друг от друга щелями создает на экране между главными максимумами до­полнительные (N-2) максимума, разделенные (N-1) минимумом. Расположение дополнительных минимумов удовлетворяет усло­вию 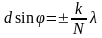, где k принимает все возможные целочислен­ные значения кроме 0, N, 2N и т. д., так как при них данное ус­ловие совпадает с условием главных максимумов. Дополнитель­ные максимумы очень малы по интенсивности и при больших N становятся практически неразличимыми на фоне ярких главных максимумов.

Если на решетку падает белый свет, то максимумы 1-го и более высоких порядков разложатся в спектры. Максимум для фиолетовых лучей будет располагаться ближе к центру экрана. Центральные нулевые максимумы для всех длин волн будут совпадать и поэтому в центре экрана будет наблюдаться белая полоса. Благодаря способности разлагать в спектр падающее из­лучение, дифракционная решетка широко используется для ис­следования спектрального состава излучения, т.е. для определе­ния длин волн и интенсивностей всех его монохроматических компонентов. По расстояниям между дифракционными линиями при заданной длине волны можно определить период решетки, а по величине интенсивностей максимумов различных порядков изучить структуру рассеивающих центров (в обычной решетке это непрозрачные промежутки шириной b).

Для визуального наблюдения и фотографирования спек­тров применяются дифракционные спектрографы с дифракци­онной решеткой. Они позволяют проводить химический анализ и изучать строение материалов.

35. Дифракция рентгеновских лучей на кристаллических структурах. Формула Вульфа – Брэгга.