50

Лабораторная работа № 7

ИЗУЧЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

И ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ

МАЯТНИКА ОБЕРБЕКА

В настоящей работе экспериментально определяется и исследуется момент инерции тела сложной геометрической формы – крестообразного маятника.

1. Описание установки и метода измерений

Прибор Обербека, применяемый в данной работе, схематически изображен на рис. 1. Крестообразный маятник состоит из четырех стержней 1 и двух шкивов 2 различного радиуса, укрепленных на одной горизонтальной оси (0). По стержням могут перемещаться и закрепляться в нужном положении четыре (по одному на каждом стержне) цилиндрических грузика 3 одинаковой массы М.

Рис. 1

При помощи грузов 4 разной массы m, прикрепленных к концу намотанной на тот или иной шкив нити, крестообразный маятник может приводиться во вращение. Высота h , с которой начинает движение груз m, отсчитывается по линейке 5, укрепленной на вертикальной стойке 6. Нить с грузом пропускается через легкий шкив 7. Время движения груза 4 с высоты h отсчитывается по секундомеру 8. Крестообразный маятник, линейка и секундомер смонтированы вместе. Секундомер, применяемый в такой установке, снабжен фотодатчиком 9, который автоматически включает его, когда груз касается опоры*. В данной установке (рис.2) используется симметричное расположение цилиндрических грузиков М на стержнях. Если пренебречь моментом сил трения в подшипниках оси, то единственной силой, которая создает момент относительно неподвижной оси вращения, является сила натяжения нити Т.

Основное уравнение динамики вращательного движения для маятника Обербека имеет вид

I = Tr, (1)

где I – момент инерции маятника;  – угловое ускорение; r – радиус шкива, на который наматывается нить.

Для поступательного движения груза m можно записать систему уравнений

ma = mg – T; , (2)

где h – высота, с которой начинает движение груз m; t – время движения груза с высоты h; a – ускорение груза в момент времени t.

Используя связь линейного и углового ускорений a =  r, получим

. (3)

Работа состоит из двух частей.

В первой устанавливается независимость момента инерции I от момента внешних сил. Изменять величину момента сил можно, изменяя радиус шкива r или массу груза m.

Во второй части работы изучается зависимость момента инерции от распределения массы тела относительно оси вращения. Из определения момента инерции следует, что оставляя массу крестообразного маятника неизменной, но изменяя при этом распределение массы относительно оси вращения, можно получить разные моменты инерции. Изменение распределения массы маятника можно осуществить, перемещая цилиндрические грузики М вдоль стержней.

__________________________________________________

*В лаборатории имеется прибор Обербека, в котором крестообразный маятник, секундомер и линейка не объединены в одну установку.

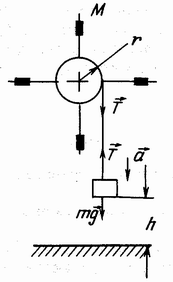
Рис. 2

2. Порядок выполнения работы

Часть 1

1. Закрепляют цилиндрические грузики М на середине стержня таким образом, чтобы система находилась в положении безразличного равновесия. Этого добиваются проверкой равновесия в двух взаимно перпендикулярных положениях крестовины: сначала один из стержней располагают горизонтально, потом другой – при этом маятник не должен вращаться.

2. Закрепляют нить с грузом m на шкиве радиуса r₁ и наматывают ее так, чтобы груз поднялся на высоту h. Высоту отсчитывают по линейке по нижнему торцу груза m.

3. Включают в сеть секундомер (кнопка СЕТЬ), при этом загорается цифровая индикация и лампочка фотодатчика. Одновременно включается тормоз, не позволяющий вращаться маятнику, и груз m фиксируется на высоте h.

4. Переключают секундомер на измерение времени (кнопка ПУСК). Одновременно отключается тормоз и груз m начинает опускаться, вращая маятник.

Внимание. Кнопка ПУСК должна быть включена все время, пока секундомер отсчитывает время движения груза. Отсчет времени автоматически прекратится после того как груз коснется опоры.

5. Записывают время t₁ движения груза m в табл. 1, отключают секундомер от сети (кнопка СЕТЬ). Повторяют опыт (п. 3–5) пять раз*.

6. Перекидывают нить с грузом на другой шкив радиуса r₂ и повторяют опыт по измерению времени t₂ движения груза с той же высоты h 5 раз (п.2 –5). Данные заносят в табл. 2.

Часть 2

1. Закрепляют нить с грузом m на шкиве радиуса r₁ и в дальнейшем эти данные не меняют.

2. Устанавливают грузики М, сдвигая их от середины ближе к оси вращения.

3. Включают секундомер и повторяют опыты (ч. 1, п. 3 – 5) по измерению времени t₃ падения груза 5 раз. Данные заносят в табл. 3.

4. Устанавливают грузики М, сдвигая их от середины к краю, дальше от оси вращения и измеряют время t₄ (табл. 4).

5. Устанавливают грузики М, сдвигая их от середины к центру ближе к оси вращения и измеряют время t₄ (табл. 4).

3. Обработка результатов измерений

1. По данным табл. 1 и 2, используя (3), вычисляют моменты инерции I₁ и I₂ и находят среднее значение .

2. По данным табл. 3 и 4 вычисляют моменты инерции I₃ и I₄. Проверяют соотношение .

Данные установки

M = M =

m = m =

r₁ = r₁ =

r₂ = r₂ =

h = h =

_______________________________________________________

*Если секундомер не соединен с установкой, то измерение времени падения груза с высоты h производится включением и выключением секундомера вручную.

Таблица 1			Таблица 2			Таблица 3			Таблица 4
М – на середине стержня						m = r1 =			m = r1 =
m = r1 =			m = r2 =			М – ближе к оси			М – дальше от оси
i	t1	t1	t2	t2		i	t3	t3	t4	t4
1 2 3 4 5						1 2 3 4 5
Среднее		–	Среднее	–		Среднее		–	Среднее	–

I=( + )/2

3. Расчет погрешности измерений t_1i = – t_1i

n = 5

t_1инс =

t₁ =

t₁ = + t₁ =

t_2сл = t_3сл = t_4сл =

t_2инс = t_3инс = t_4инс =

t₂ = t₃ = t₄ =

t₂ =  t₂ = t₃ =  t₃ = t₄ =  t₄ =

;

;

;

.

Сравнивают I₄, I₃, I .

Определяют относительную погрешность .

Контрольные вопросы

1. Что изменится в системе уравнений (1) и (2) и в формуле (3) для расчета I, если учесть силу трения в опоре?

2. Как из закона сохранения полной механической энергии системы можно найти скорость груза при ударе об опору?

3. При каких условиях в этой системе выполняется закон сохранения механической энергии?

4. Как, используя закон изменения полной механической энергии системы, можно определить работу сил трения в системе?