Описание лабораторных работ / Лабораторная работа 12

79

Лабораторная работа № 12

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ПЛОСКОГО

ФИЗИЧЕСКОГО МАЯТНИКА

Цель работы – изучение колебательного движения физического маятника, а также определение его момента инерции.

1. Описание установки и метода измерения

Схема установки приведена на рис. 1. Некоторое тело может свободно колебаться вокруг оси, закрепленной на подставке.

Такая система представляет собой физический маятник, колебания которого близки к гармоническим при малых амплитудах этих колебаний.

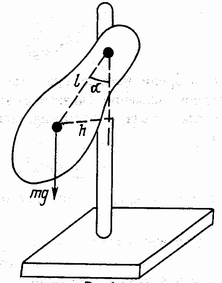
Рис.1

Найдем период таких колебаний. Если маятник отвести от положения равновесия на малый угол , то на него будет действовать возвращающий момент силы M= –mg h= –mg sin. Здесь  – расстояние от центра масс тела до оси вращения; h – плечо силы тяжести mg. Запишем основное уравнение динамики вращательного движения

I = –mg sin  . (1)

Знак – связан с тем, что угол  откладывается по часовой стрелке, а возвращающий момент силы тяжести пытается повернуть тело против часовой стрелки.

Так как , а при малых углах отклонения sin, то уравнение (1) можно преобразовать к виду

. (2)

Если ввести обозначения , то получим уравнение

, (3)

которое описывает процесс колебаний тела с угловой частотой

и периодом колебаний

. (4)

Здесь I – момент инерции тела, который характеризует его инертные свойства во вращательном движении. Он зависит как от массы тела, так и от ее распределения по объему тела относительно оси вращения. По определению момент инерции

, (5)

где  m_i – масса элемента тела; r_i – расстояние от оси вращения до этого элемента.

Для непрерывного распределения массы = .

Однако для определения момента инерции воспользуемся не формулой (5), которая удобна для теоретических расчетов, а формулой (4), из которой момент инерции тела

. (6)

Таким образом, для определения момента инерции необходимо измерить период колебаний тела, найти его массу и определить расстояние от оси вращения до центра масс тела. Точку центра масс можно найти как точку пересечения двух вертикальных линий, которые можно нанести, подвешивая тело за две разные оси (рис. 2).

Рис. 2

Ускорение свободного падения на широте Москвы принимается

g= 9,8156 м/с².

Если I₁ – момент инерции тела относительно оси 1, а I₂ – относительно оси 2, то согласно теореме Штейнера

. (7)

Здесь I₀ – момент инерции маятника относительно оси центра масс; ₁ и ₂ – расстояния от центра масс до осей 1 и 2. Решив систему уравнений (7), можно найти момент инерции тела относительно оси, проходящей через центр масс

. (8)

2. Порядок выполнения работы

Момент инерции тела определяется для двух осей – оси 1 и 2 (см. рис. 2).

1. Закрепите тело на подставке относительно оси 1. Отклонив маятник на малый угол, убедитесь, что до полной остановки он совершает не менее 15 колебаний.

2. Измерьте время  десяти полных колебаний. Опыт повторить 5 раз. Данные занести в таблицу. По среднему времени и числу колебаний n рассчитать период колебаний маятника .

3. Аналогичные измерения проведите для оси 2.

4. Определите расстояние ₁ и ₂ от осей вращения 1 и 2 до центра масс тела. Для этого свободно закрепите тело на оси 1 и с помощью нити с грузом отметьте положение первой вертикальной линии. Подвесив тело на оси 2, найдите вторую вертикальную линию. Точка их пересечения и есть центр масс тела.

5. С помощью линейки найдите расстояние ₁ и ₂ от осей вращения до центра масс. Каждое из измерений провести один раз. Предельная инструментальная погрешность   не менее 1 мм.

Данные установки и таблица результатов измерений

Масса тела m = ;  m = .

Расстояния от осей вращения до центра масс:

₁ = ,  ₁ =

₂ = ,  ₂ =

 _инс = .

Таблица

№	Ось 1		Ось 2
	1	 1i	2	 2i
1 2 3 4 5
Среднее		–		–

3. Обработка результатов измерений

1. Вычислите значения моментов инерции I₁ и I₂ по формуле (6).

2. Найдите случайные погрешности ₁ и ₂ по обычным правилам.

3. Найдите суммарную погрешность времени 

.

Так как , то .

4. Найдите погрешность косвенных измерений по формуле

.

4. Запишите окончательный результат измерений

с учетом правил округления.

4. По формуле (8) определите момент инерции тела относительно оси, проходящей через центр масс.

Погрешность измерения  I₀ определите по формуле

.

Запишите значение I₀ с учетом правил округления

.

Контрольные вопросы

1. Что характеризует момент инерции тела? От каких параметров тела он зависит?

2. Почему в данной работе ?

3. Запишите основное уравнение динамики вращательного движения и охарактеризуйте каждую из величин, входящих в это уравнение.

4. Выведите формулу для периода колебаний физического маятника.

5. Докажите, что период колебаний однородного физического маятника не зависит от его массы (на примере колебаний диска или кольца).