Теоретический анализ.
4.1 Постановка задачи на нахождение эффективных коэффициентов распределения примесей
Наиболее простой анализ распределения примесей основан на приближении полного конвективно-диффузионного перемешивания расплава, согласно которому концентрация примеси в слитке определяется её исходной концентрацией в расплаве С0, долей закристаллизовавшейся части f, не зависящим от концентрации эффективным коэффициентом распределения k в соответствии с уравнением Пфанна:
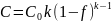(6)
В действительности интенсивность свободной конвекции, характеризуемая соотношением Vδ/D~1, не достаточна, чтобы обеспечить однородность жидкой фазы (V – скорость роста, в среднем равная скорости перемещения системы тигель-расплав-кристалл; δ - толщина диффузионного слоя; D - коэффициент диффузии примеси в расплаве ~10-8 м2/с). Влияние диффузии может проявляться в следующем:
а) При кристаллизации идёт процесс насыщения диффузионного пограничного слоя в расплаве до стационарного состояния. Если не считать объём расплава конечным, то в приближении чистой диффузии распределение примеси можно описать уравнением вида:
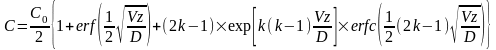(7)
где вместо доли закристаллизовавшегося расплава f аргументом функции выступает z – расстояние от начала роста кристалла до центра определения концентрации; V - скорость роста; D - коэффициент диффузии. Графики функций (1) и (2) при равных k и С0 начинаются в точке z=0 и пересекаются при некотором f →1 (рис. 1). б) Увеличение толщины диффузионного пограничного слоя δ будет повышать эффективный коэффициент распределения примеси согласно соотношению Бартона-Прима-Слихтера:
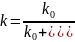(8)
где k0 – равновесный коэффициент распределения [2].
Исходя из того, что на распределение примеси в слитке оказывает влияние её диффузия в расплаве, имеющая место в режиме свободной конвекции (Vδ/D~1), при аппроксимации экспериментальных данных функцией (1) в работе предложено ориентироваться на точки C(f), относящиеся к верхней половине слитка (f≥0,5).
Рисунок.18 Распределение Ge в кремнии при разных режимах направленной кристаллизации: 1 – чистая диффузия (Vδ/D>>1), 2 - полное перемешивание (Vδ/D<<1), 3 – свободная конвекция (Vδ/D~1). f - доля закристаллизовавшейся части
5. Обсуждение результатов
5.1 Нахождение эффективных коэффициентов распределения примесей
Поскольку погрешности определения микроконцентраций примесей в слитке являются существенными, то распределение Пфанна (1) также приводится при С0±Δ, где Δ погрешность, указанная в методике ИСП-МС для соответствующего интервала значений концентраций по конкретному элементу. Дело в том что погрешность в определении на порядки большего значения исходной концентрации примеси существенно ниже погрешностти определения концентрации данной примеси в слитке, тем более, что значение С0 пересчитаны исходя из состава лигатуры, добавляемой в полупроводниковый кремний. Значение коэффициента распределения примеси подбиралось таким, чтобы аппроксимирующие кривые (1) при С0-Δ и при С0+Δ не выходили за границы интервалов, в которых находится погрешность измерения концентрации примеси в нижней и верхней частях слитков, соответственно (графики.19,20,21). На графиках.19,20,21 приведены распределения примесей Ge, Mn, Co, Fe, Ni, V в слитке №3, показывающие результат влияния диффузионного переноса вещества.
Экспериментальные профили распределения вынести в отдельное приложение.
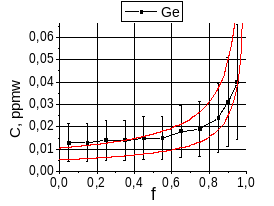
График.19
Распределение примесей Ge
(k=
),
Mn
(в
ppmw
или
масс.%)
по высоте слитка mc-Si
на основе загрузки №3.
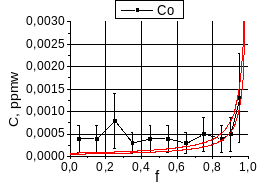
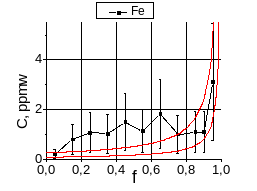
График.29 Распределение примесей Co, Fe
(в ppmw или масс.%) по высоте слитка mc-Si
на основе загрузки №3.
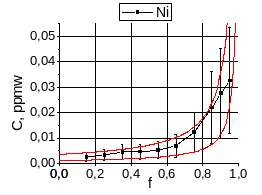
Рисунок.21 Распределение примесей Ge (k= ) Ni, V
(в ppmw или масс.%) по высоте слитка mc-Si
на основе загрузки №3
Немонотонное
изменение концентрации по мере увеличения
закристаллизовавшейся доли f
на некоторых может быть связано с
локальными колебаниями концентрации
примеси в пограничном слое при неполном
перемешивании расплава в режиме свободной
конвекции. Также на локальные особенности
диффузионного пограничного слоя
оказывает влияние механизм роста
кристалла. Кремний на границе
кристалл-расплав имеет как атомно-гладкие
плотноупакованные поверхности [11], так
и атомно-шероховатые (любые другие
кристаллографические плоскости.) Сильное
переохлаждение
4К
на гранях [11] вызывает большие скорости
тангенциального роста.
В таблице приведены эффективные коэффициенты распределения примеси германия и группы железа. Прочерки в табл. 2 связаны с пределами обнаружения примесей, либо просто отсутствием данных по содержанию конкретного элемента [18].
Таблица.2
Эффективные коэффициенты распределения примесей при выращивании mc-Si из MG-Si [18] и на основе загрузок №1-4
|
Fe |
Ni |
V |
Ge |
Mn |
Co |
mc-Si из MG-Si [2] |
0,0004 |
0,0015 |
- |
- |
0,002 |
- |
mc-Si из загрузки №1 |
0,002 |
0,006 |
0,00004 |
0,33 |
0,001 |
0,00001 |
mc-Si из загрузки №2 |
0,025 |
0,012 |
0,002 |
0,33 |
0,03 |
0,0005 |
mc-Si из загрузки №3 |
0,03 |
0,015 |
0,0012 |
0,33 |
0,017 |
0,0002 |
mc-Si из загрузки №4 |
0,05 |
0,02 |
0,003 |
0,33 |
0,035 |
0,0006 |
Высокие
значения эффективных коэффициентов
распределения отдельно взятых примесей
группы железа по сравнению с соответствующими
равновесными равновесных коэффициентов
распределения
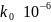обусловлены неравновесными условиями
роста [18]. Когда концентрации достаточно
высоки, то между примесными частицами
начинается взаимодействие в твёрдой
фазе, которое ведёт к зависимости
коэффициента распределения (табл.2) от
концентрации (табл.1). Объяснить её можно
тем, что внедрение примесной частицы в
решётку, уже деформированную другой
частицей, требует большой работы, чем
внедрение в недеформированную решётку.
Это упругое взаимодействие уменьшает
растворимость в кристалле и уменьшает
коэффициент распределения, начиная с
некоторых концентраций. В результате
чего коэффициент распределения при
больших концентрациях примеси уменьшается
[21]. Когда линии ликвидус и солидус в
области малых концентраций практически
прямолинейны, то k
не зависит от С0. По табл.1 и 2 это можно
наблюдать для примеси Ge,
образующим с кремнием непрерывный ряд
твёрдых растворов. Также видно, что
указанной выше закономерности не
соответствует значение примеси Mn
авторов работы [18]. Вероятно, что существует
некая особенность физико-химического
взаимодействия различных примесей при
встраивании их в кристаллическую
структуру слитка, характеризующаяся
вопреки рассуждениям выше. Кроме того,
при сопоставимых соотношениях градиента
температуры к скорости кристаллизации
MG-Si
(G/V=4*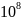
K*c/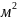
)
и кремния состав №1-4 (G/V=3,6*
K*c/
),
имеется различие в тепловом поле и в
геометрии системы тигель-расплав-кристалл
(табл.3). В частности, вогнутая форма
кристаллизации способствует захвату
примеси в растущем кристалле [20].
В
целом чтобы не происходило возрастание
эффективного коэффициента распределения
примеси, необходимо снижать значение
её конвективно-диффузионного параметра
V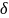
/D
за счёт :а) снижения скорости кристаллизации
V;
б) иного внешнего воздействия на
тепломассоперенос для увеличения
градиента температуры G
на границе раздела фаз и уменьшения тем
самым толщены диффузионного слоя
.
Заключение
Установлен характер распределения примесей в слитках мультикристаллического кремния, показывающей, что при направленной кристаллизации имеет место как конвективный, так и диффузионный перенос вещества. Исследования распределения примесей ряда железа показывает, что уменьшение концентраций в исходном кремнии до пределов растворимости и ниже ведёт к возрастанию эффективных коэффициентов распределения примесей. С целью не допустить возрастания эффективного коэффициента распределения примеси, одновременно с повышением частоты исходного кремния необходимо снижать распределение примеси, необходимо снижать значение её конвективно-диффузионного параметра V /V за счёт воздействия на тепломассоперенос при направленной кристаллизации.
Список используемых источников
1.Грибов Б.Г., Зиновьев К.В. Получение высокочистого кремния для солнечных элементов. // Неорганические материалы. – 2003. – Т. 39. - №7. – С. 775-785.
2.Istratov A.A., Buonassisi T., Pickett M.D., Heuer M., Weber E.R. Control of metal impurities in “dirty” multicrystalline silicon for solar cells. // Materials Science and Engineering B. – 2006. – V. 134. - № 2-3. – P. 282-286.
3.Басин А.С., Шишкин A.В. Получение кремниевых пластин для солнечной энергетики: Методы и технологии. Новосибирск, Институт теплофизики СО РАН. – 2000. - с. 87.
4.Нашельский А.Я., Пульнер Э.О. Современное состояние технологии кремния для солнечной энергетики. // Высокочистые вещества. – 1996. - № 1. – С. 102-110.
5.Bathey B.R., Cretella M.C. Review solar grade silicon. // Journal of Materials Science. – 1982. - V. 17. – № 11. - P. 3077-3096.
6.Диссертациииияяя
7.Мюллер Г. Выращивание кристаллов из расплава: Конвекция и неоднородность: Пер. с англ. - М.: Мир. - 1991. - 143 с. - ил.
8.Лысенко Л.Н. Использование нейтральных примесей, компенсированных основой, для производства монокристаллов кремния. Канд. диссертация. М.: - 2001. – 239 с.
9.K.A. Jackson. Constitutional supercooling surface roughening // Journal of Crystal Growth. - 2004. - V. 264. - № 4. - P. 519-529.
10.Fujiwara K., Obinata Y., Ujihara T., Usami N., Sazaki G., Nakajima K. Grain growth behaviors of polycrystalline silicon during melt growth processes. // Journal of Crystal Growth. - 2004. - V. 266. - № 4. - С. 441-448.
11.Пресняков Р.В., Непомнящих А.И., Бердников В.С. Влияние режима роста на макроструктуру мультикристаллического кремния. / Тезисы докладов VIII международной конференции и VII школы молодых учёных «Кремний-2011». Москва: Изд-во МИсиС. - 2011. - C. 60-61.
12 Fujiwara K., Pan W., Usami N., Sawada K., Tokairin M., Nose Y., Nomura A., Shishido T., Nakajima K. Growth of structure-controlled polycrystalline silicon ingots for solar cells by casting. // Acta Materialia. - 2006. – V. 54, - № 12. – P. 3191-3197.
13.Нашельский А.Я., Пульнер Э.О. Получение слитков и пластин кремния для солнечных батарей. // Высокочистые вещества– 1996. - № 5. – С. 47-55.
14. Nose Y., Takahashi I., Pan W., Usami N., Fujiwara K., Nakajima K. Floating cast method to realize high-quality Si bulk multicrystals for solar cells. Journal of Crystal Growth. - 2009. - V. 311. - № 2. - С. 228-231.
15. Hopkins R.H., Davis J.R., Rohatgi A., Campbell R.B., Blais P.D., Rai-Choudhury P., Stapleton R.E., Mollenkopf H.C., McCormick // Westinghouse report, Phase III, Vol. 2, JPL Contract No. 954331, January, 1980 (USA).
16.Горелик С.С., Дашевский М.Я. Материаловедение полупроводников и диэлектриков: Учебник для вузов. – М.: МИСиС, 2003. – 480 с.
17.Современные масс-спектрометры высокого разрешения для прецизионного элементного анализа в индуктивно связанной аргоновой плазме и источнике тлеющего разряда/ С.Лапшин., О.Прошенкина/ оборудование и материалы. 2012(4) —№1 — С. 28 — 36.
18. Martorano M.A., Oliveira T.S., Ferreira Neto J.B., Tsubaki T.O. Macrosegregation of impurities in directionally solidified silicon // Metallurgical and Materials Transactions A: Physical Metallurgy and Materials Science. 2011. V. 42. № 7. P. 1870-1886.
19.Непомнящих А.И., Пресняков Р.В., Антонов П.В., Бердников В.С. Влияние скорости вращения тигля на рост и макроструктуру мультикристаллического кремния // Неорганические материалы. 2014. Т. 50. № 12. С. 1281-1286.
20.Непомнящих А.И., Пресняков Р.В., Елисеев И.А., Сокольникова Ю.В.. Особенности роста мультикристаллического кремния из металлургического кремния высокой чистоты // Письма в ЖТФ. 2011. Т. 37. № 15. С. 103-108.
21. Чернов А.А., Гиваргизов Е.И., Багдасаров Х.С. и др. Современная кристаллография. Т.3. Образование кристаллов. М.: Наука. 1980. 407 с.
Приложение А
Диапазоны измерения, характеристики погрешности,
нормативы контроля и категории точности методики
Т а б л и ц а А.1 – Диапазоны измерения, характеристики погрешности, нормативы контроля и категории точности методики для кремния кристаллического (при доверительной вероятности Р=0,95)
10-4 %
Определяемый элемент |
Диапазон измерения |
Показатель точности (границы интервала, в котором находится погрешность измерения) ±Δл |
Показатель правильности (границы интервала, в котором находится систематическая погрешность измерения) ±Δсл |
Показатели прецизионности |
Нормативы контроля прецизионности |
Категория точности |
||||||||||
среднеквадратическое отклонение повторяемости σr |
среднеквадра-тическое от-клонение внутрилабо-раторной прецизионности σRл |
предел повторяемо-сти r |
предел внутри- лабораторной прецизион-ности Rл |
|
||||||||||||
Ванадий |
От 0,10 до 0,60 вкл Св.0,60 до 3,60 вкл Св.3,6 до 20,0 вкл Св.20,0 до 100,0 вкл Св.100 до 500 вкл |
0,67 Х 0,44 Х 0,29 Х 0,20 Х 0,14 Х |
0,26 Х 0,16 Х 0,10 Х 0,066 Х 0,043 Х |
0,11 Х 0,084 Х 0,066 Х 0,053 Х 0,043 Х |
0,32 Х 0,21 Х 0,14 Х 0,10 Х 0,069 Х |
0,30 Х 0,23 Х 0,18 Х 0,15 Х 0,12 Х |
0,89 Х 0,59 Х 0,40 Х 0,28 Х 0,19 Х |
IV III III II II |
||||||||
Германий |
От 0,002 до 0,050 вкл Св.0,05 до 0,50 вкл Св.0,50 до 5,0 вкл |
0,64 Х 0,48 Х 0,32 Х |
0,33 Х 0,21 Х 0,099 Х |
0,20 Х 0,13 Х 0,059 Х |
0,28 Х 0,22 Х 0,16 Х |
0,55 Х 0,35 Х 0,16 Х |
0,78 Х 0,62 Х 0,45 Х |
IV III III |
||||||||
Железо |
От 5,0 до 25,0 вкл Св.25,0 до 125 вкл Св.125 до 700 вкл Св.700 до 3500 вкл Св.3500 до 20000 вкл |
0,76 Х 0,51 Х 0,34 Х 0,23 Х 0,15 Х |
0,28 Х 0,19 Х 0,12 Х 0,080 Х 0,051 Х |
0,14 Х 0,10 Х 0,075 Х 0,056 Х 0,040 Х |
0,36 Х 0,24 Х 0,16 Х 0,11 Х 0,072 Х |
0,39 Х 0,29 Х 0,21 Х 0,15 Х 0,11 Х |
1,00 Х 0,68 Х 0,45 Х 0,30 Х 0,20 Х |
IV III III III III |
||||||||
Кобальт |
От 0,010 до 0,070 вкл Св.0,070 до 0,50 вкл Св.0,50 до 3,50 вкл Св.3,5 до 25,0 вкл Св.25,0 до 200 вкл |
0,61 Х 0,40 Х 0,27 Х 0,18 Х 0,12 Х |
0,17 Х 0,12 Х 0,083 Х 0,057 Х 0,039 Х |
0,14 Х 0,11 Х 0,085 Х 0,066 Х 0,050 Х |
0,31 Х 0,21 Х 0,14 Х 0,088 Х 0,057 Х |
0,39 Х 0,30 Х 0,24 Х 0,18 Х 0,14 Х |
0,87 Х 0,57 Х 0,37 Х 0,25 Х 0,16 Х |
IV III II II II |
||||||||
Марганец |
От 0,020 до 0,20 вкл Св.0,20 до 2,0 вкл Св.2,0 до 20,0 вкл Св.20,0 до 200,0 вкл Св.200 до 500 вкл |
0,74 Х 0,48 Х 0,32 Х 0,21 Х 0,17 Х |
0,31 Х 0,18 Х 0,10 Х 0,060 Х 0,046 Х |
0,17 Х 0,11 Х 0,077 Х 0,053 Х 0,043 Х |
0,34 Х 0,23 Х 0,15 Х 0,098 Х 0,080 Х |
0,46 Х 0,32 Х 0,22 Х 0,15 Х 0,12 Х |
0,94 Х 0,62 Х 0,41 Х 0,27 Х 0,22 Х |
IV III III II II
|
||||||||
Никель |
От 0,02 до 0,20 вкл Св.0,20 до 2,0 вкл Св.2,0 до 20,0 вкл Св.20,0 до 150,0 вкл Св.150 до 350 вкл |
0,64 Х 0,42 Х 0,27 Х 0,19 Х 0,16 Х |
0,25 Х 0,15 Х 0,088 Х 0,055 Х 0,043 Х |
0,16 Х 0,10 Х 0,067 Х 0,046 Х 0,038 Х |
0,31 Х 0,21 Х 0,14 Х 0,093 Х 0,077 Х |
0,43 Х 0,28 Х 0,19 Х 0,13 Х 0,10 Х |
0,86 Х 0,57 Х 0,37 Х 0,26 Х 0,21 Х |
IV III III II II |
||||||||
|
||||||||||||||||
Приложение Б
Диапазоны измерения, характеристики погрешности,
нормативы контроля и категории точности методики
Т а б л и ц а А.2 – Диапазоны измерения, характеристики погрешности, нормативы контроля и категории точности
методики для оксида кремния и кварца (при доверительной вероятности Р=0,95)
10-4 %
Определяемый элемент |
Диапазон измерения |
Показатель точности (границы интервала, в котором находится погрешность измерения) ±Δл |
Показатель правильности (границы интервала, в котором находится систематическая погрешность измерения) ±Δсл |
Показатели прецизионности |
Нормативы контроля прецизионности |
Категория точности |
||||||||
среднеквадратическое отклонение повторяемости σr |
среднеквадра-тическое от-клонение внутрилабораторной прецизионности σRл |
предел повторяемости r |
предел внутри- лабораторной прецизион-ности Rл |
|||||||||||
Ванадий |
От 0,0060 до 0,032вкл Св.0,032 до 0,170 вкл Св.0,17 до 0,80 вкл Св.0,80 до 6,0 вкл |
0,64 Х 0,42 Х 0,28 Х 0,17 Х |
0,22 Х 0,13 Х 0,076 Х 0,040 Х |
0,16 Х 0,12 Х 0,085 Х 0,058 Х |
0,32 Х 0,21 Х 0,15 Х 0,090 Х |
0,44 Х 0,32 Х 0,24 Х 0,16 Х |
0,89 Х 0,59 Х 0,40 Х 0,25 Х |
IV III III II |
||||||
Германий |
От 0,20 до 0,60 вкл Св.0,60 до 1,20 вкл Св.1,20 до 1,80 вкл Св.1,80 до 2,30 вкл |
0,34 Х 0,24 Х 0,17 Х 0,13 Х |
0,13 Х 0,12 Х 0,11 Х 0,10 Х |
0,093 Х 0,069 Х 0,054 Х 0,045 Х |
0,17 Х 0,10 Х 0,065 Х 0,042 Х |
0,26 Х 0,19 Х 0,15 Х 0,13 Х |
0,46 Х 0,29 Х 0,18 Х 0,12 Х |
III III II II |
||||||
Железо |
От 2,00 до 20,0 вкл Св.20,0 до 200,0 вкл Св.200 до 2000 вкл Св.2000 до 5000 вкл |
0,65 Х 0,45 Х 0,31 Х 0,26 Х |
0,23 Х 0,13 Х 0,078 Х 0,059 Х |
0,097 Х 0,058 Х 0,034 Х 0,026 Х |
0,32 Х 0,23 Х 0,16 Х 0,14 Х |
0,27 Х 0,16 Х 0,095 Х 0,073 Х |
0,87 Х 0,62 Х 0,44 Х 0,37 Х |
IV III III III
|
||||||
Кобальт |
От 0,0070 до 0,030вкл Св.0,030 до 0,150 вкл Св.0,15 до 1,00 вкл Св.1,0 до 6,0 вкл Св.6,0 до 80,0 вкл |
0,69 Х 0,50 Х 0,35 Х 0,25 Х 0,15 Х |
0,22 Х 0,14 Х 0,082 Х 0,049 Х 0,024 Х |
0,14 Х 0,11 Х 0,087 Х 0,067 Х 0,047 Х |
0,33 Х 0,25 Х 0,18 Х 0,13 Х 0,082 Х |
0,39 Х 0,31 Х 0,24 Х 0,19 Х 0,13 Х |
0,92 Х 0,69 Х 0,49 Х 0,36 Х 0,23 Х |
IV III III III II
|
|
|||||
Марганец |
От 0,040 до 0,20 вкл Св.0,20 до 1,0 вкл Св.1,0 до 5,0 вкл Св.5,0 до 30,0 вкл |
0,72 Х 0,47 Х 0,30 Х 0,19 Х |
0,27 Х 0,14 Х 0,075 Х 0,038 Х |
0,14 Х 0,090 Х 0,057 Х 0,034 Х |
0,34 Х 0,23 Х 0,15 Х 0,098 Х |
0,40 Х 0,25 Х 0,16 Х 0,094 Х |
0,94 Х 0,63 Х 0,42 Х 0,27 Х |
IV III III II |
|
|||||
Никель |
От 0,010 до 0,150 вкл Св.0,15 до 1,50 вкл Св.1,5 до 10,0 вкл |
0,71 Х 0,49 Х 0,36 Х |
0,32 Х 0,18 Х 0,11 Х |
0,11 Х 0,080 Х 0,062 Х |
0,32 Х 0,24 Х 0,18 Х |
0,30 Х 0,22 Х 0,17 Х |
0,90 Х 0,66 Х 0,51 Х |
IV III III |
|
|||||