Основные параметры зубчатых колёс

Основными параметрами зубчатого колеса являются (рис. 75):

рис. 75

z – число зубьев;

r_a – радиус (диаметр) окружности

выступов;

r_f – радиус (диаметр) окружности

впадин;

r_b - радиус (диаметр) основной окружности;

r - радиус (диаметр) делительной окружности, т. е. окружности, которая является начальной в станочном зацеплении колеса с режущим инструментом;

р – шаг по делительной окружности;

h – высота зуба, равная h=h_a+h_f, где:

h_a – высота головки зуба;

h_f – высота ножки зуба;

m – модуль зацепления, определяемый из условия:

, т. е.   (измеряется в мм).

Величина m стандартизирована, а делительная окружность является окружностью стандартного модуля.

Обычно размеры зубчатого колеса и зубьев выражаются через m.

Так, например:  , где   - коэффициент высоты головки зуба;

, где   - коэффициент радиального зазора;

;  ;  , где α – угол исходного контура режущего инструмента.

Обычно для стандартных зубчатых колёс:  ;  ; α=20º.

Свойства и характеристики эвольвентного зацепления цилиндрических зубчатых колес. Условия отсутствия интерференции зубьев.

Эвольвента обладает следующими свойствами, которые используются в теории зацепления:

1) форма эвольвенты определяется радиусом основной окружности;

2) нормаль к эвольвенте в любой ее точке является касательной к основной окружности. Точка касания нормали с основной окружностью является центром кривизны эвольвенты в рассматриваемой точке;

3) эвольвенты одной и той же основной окружности являются эквидистантными(равноотстоящими друг от друга) кривыми.

Интерференция профилей приводит к заклиниванию зубьев одного колеса во впадинах другого. Для исключения интерференции в эвольвентном зацеплении точки касания профилей зубьев колес должны всегда находиться на линии зацепления, что обеспечивается при угле профиля α = 20° числом зубьев колес больше 17.

При нарезании эвольвентных зубчатых колес с числами зубьев меньше 17 имеет место интерференция части профиля зуба колеса и профилей зубьев режущего инструмента. В этом случае режущие кромки инструмента срезают часть формообразующей кривой профилей зубьев колеса.

Качественные показатели эвольвентного зацепления цилиндрических зубчатых колес.

Качественные показатели цилиндрической эвольвентной передачи.

К качественным показателям цилиндрической эвольвентной зубчатой передачи относятся:

• коэффициент торцевого перекрытия

• коэффициент полезного действия

• коэффициент удельного скольжения

• коэффициент удельного давления

• коэффициент формы зуба

Рассмотрим эти коэффициенты подробнее (исключив из рассмотрения коэффициент полезного действия, как величину характеризующую реальные, а не рассматриваемые нами идеализированные механизмы).

Коэффициент торцевого перекрытия

Коэффициентом перекрытия eg называется величина отношения угла перекрытия зубчатого колеса к его угловому шагу, где под углом перекрытия понимают угол на который поворачивается колесо за время зацепления одной пары зубьев. Для цилиндрических колес различают полное eg, торцевое ea и осевое перекрытие:

где осевое перекрытие имеется только в косозубых передачах.

где,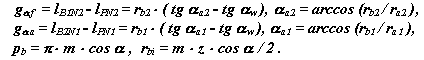 

Коэффициент перекрытия определяет величину зоны двухпарного контакта, когда одновременно зацепляются два последовательно расположенных зуба. Так как до окончания зацепления одной пары зубьев, следующая пара должна войти в контакт, нельзя допускать в прямозубых передачах  . Допустимое значение коэффициента перекрытия должно несколько превышать единицу и, в зависимости от назначения передачи и точности ее изготовления, выбирается в пределах  . Максимальное значение коэффициента перекрытия для зубчатых колес, обработанных инструментом со стандартным исходным производящим контуром, составляет  . Наиболее благоприятны величины коэффициента перекрытия равные целым числам, например двум или трем. Обеспечить это можно только используя инструмент с нестандартным исходным производящим контуром. Дробные значения коэффициента перекрытия, например близкие к полутора, приводят к циклическому изменению жесткости передачи и к возникновению параметрических колебаний.