26. Трение скольжения во вращательной кинематической паре. Круг трения. Приведённый коэффициент трения

а – радиус круга трения.

Полная реакция “R” касается круга трения радиуса “a”.

Он имеет тот же смысл, что и конус трения в

поступательной паре.

При силовом анализе удобнее считать, что

полная реакция “R”

проходит через центр “O”. Тогда для учета трения надо

добавить момент трения.

   .

Для малых углов   , тогда:

Реально коэффициент трения   между цилиндрическими поверхностями больше, чем между плоскими.

Поэтому:

 ,   - приведенный коэффициент трения во вращательной паре.

1)   - для новых неприработавшихся пар.

2)   - для приработавшихся пар.

Потери мощности на трение во вращательной паре:

30) Механический кпд и коэффициент потерь. КПД при последовательном и параллельном соединении механизмов.КПД – это мера эффективности механизма, определяемая отношением полезной работы к подведенной при его работе (полной), т.е. h=A_пс (полезного сопротивления)/A_дв (движущие силы), т.к. A_дс=А_сп+А_св, то h=(А_дс–А_св)/А_дс = 1–А_св/А_дс = 1–y, где y – коэффициент потерь. При последовательно соединенных механизмах общий КПД равен произведению КПД всех механизмов и применение механизма с низким КПД не выгодно. При параллельном соединении механизмов A_дν_n=A_д1, η_n=A_n/ A_дν_n при этом один из механизмов будет с малым КПД.

Механический КПД и коэффициент потерь. КПД при последовательном и параллельном соединении механизмов.

Часто для выполнения необходимой работы в машине применяется несколько разных механизмов, соединенных между собой.

Рассмотрим порядок расчета коэффициента полезного действия при последовательном и параллельном соединении механизмов.

Кпд при последовательном соединении механизмов

Последовательное соединение (рисунок 30).

Рисунок 30

В этом случае движение (и мощность) передается последовательно от одного механизма к другому. Полезной работой для предыдущего механизма является приведение в движение следующего. То есть полезная работа на выходе предыдущего механизма является одновременно движущей для последующего. Полезной работой всей системы является работа на выходе из последнего механизма системы:

Таким образом, общий коэффициент полезного действия системы последовательно соединенных механизмов равен произведению коэффициентов полезного действия этих механизмов:

Так как КПД любого механизма меньше единицы, то КПД системы последовательно соединенных механизмов оказывается всегда ниже худшего из механизмов этой системы. Поэтому, если применяется система последовательных механизмов (или отдельных элементов), то не следует включать в эту систему механизмы с низкими КПД.

Если последовательно соединяется "n" одинаковых механизмов:

то

где  η_P – КПД любого промежуточного механизма.

Кпд при параллельном соединении механизмов

Параллельное соединение ( рисунок 31).

Рисунок 31

Несколько механизмов приводятся в движение одним двигателем. Полезная работа системы складывается из полезных работ на выходе из каждого механизма. На приведение в движение каждого из механизмов двигатель затрачивает часть своей энергии (А_ДВ i ). Тогда коэффициент полезного действия такой системы можно представить следующим образом:

В данном случае величина общего кпд зависит от доли энергии, отдаваемой двигателем механизмам с более высокими  или более низкими кпд. Но во всех случаях общий КПД занимает некоторое промежуточное значение по отношению к частным КПД механизмов, соединенных в систему (КПД системы будет тем выше, чем большая часть энергии двигателя будет отдаваться механизмам с высокими КПД).

Если параллельно соединяется "n" одинаковых механизмов:

При параллельном соединении одинаковых механизмов КПД системы не изменяется и равен КПД одного механизма.

КПД передачи винт - гайка, Самоторможение. КПД червячной передачи.

КПД передачи “Винт - гайка”.

Передачу “винт - гайка” приближенно можно представить в виде ползуна, движущегося по наклонной плоскости, которая получается путем развертки средней винтовой линии резьбы на плоскость.

   - угол наклона средней винтовой линии.

 - угол трения.

h – ход винтовой линии.

p – шаг резьбы.

z – число заходов.

 ;

При прямом ходе винт преодолевает осевую нагрузку   :

F – движущая сила.

R – полная реакция.

При равномерном движении:

Силовой треугольник:

 или 

При   

Самоторможение в передаче винт-гайка.

В этом случае под действием силы F_a гайка не может поворачиваться (из-за трения) относительно неподвижного винта. Условие самоторможения

 .

Формула) определяет условие самоторможения, а именно для са­моторможения передачи винт-гайка необходимо, чтобы угол подъема вин­товой линии резьбы (   ) был меньше приведенного угла трения   .

Определение угла   :

 — угол трения; (4)

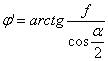 - приведенный угол трения. (5)

Динамическое и статическое уравновешивание вращающихся звеньев. Виды неуравновешенности, их оценка и способы устранения. Балансировка.

 Уравновешивание и балансировка вращающихся масс.

 

Цели уравновешивания и балансировки

При движении звеньев с переменными скоростями (с ускорением) возникают силы инерции и их моменты, которые принято называть динамическими нагрузками. Их возникновение приводит к вибрации и шуму. Причинами возникновения вибраций могут быть периодические изменения сил (силовое возмущение), перемешений (кинематическое возмущение) или инерционных характеристик (параметрическое возмущение). Вибрацией (от лат. vibratio - колебание) называют механические колебания в машинах или механизмах. Колебание - движение или изменение состояния, обладающие той или иной степенью повторяемости или периодичностью. Если источник возникновения вибраций определяется внутренними свойствами машины или механизма, то говорят о его виброактивности. Чтобы вибрации механизма не распространялись на окружающие его системы или чтобы защитить механизм от вибраций, воздействующих на него со стороны внешних систем, применяются различные методы виброзащиты. Различают внешнюю и внутреннюю виброактивность. Под внутренней виброактивностью понимают колебания возникающие внутри механизма или машины, которые происходят по его подвижностям или обобщенным координатам. Эти колебания не оказывают непосредственного влияния на окружающую среду. При внешней виброактивности изменение положения механизма приводит к изменению реакций в опорах (т.е. связях механизма с окружающей средой) и непосредственному вибрационному воздействию на связанные с ним системы. Одна и основных причин внешней виброактивности - неуравновешенность его звеньев и механизма в целом, которое устраняется уравновешиванием звеньев при проектировании механизма. Это достигается соответствующим подбором масс и моментов инерции.

Неуравновешенным будем называть такой механизм (или его звено), в котором при движении центр масс механизма (или звена) движется с ускорением. Так как ускоренное движение системы возникает только в случае, если равнодействующая внешних силовых воздействий не равна нулю. Согласно принципу Д’Аламбера, для уравновешивания внешних сил к системе добавляются расчетные силы - силы и моменты сил инерции. Поэтому уравновешенным будем считать механизм, в котором главные вектора и моменты сил инерции равны нулю, а неуравновешенным механизм, в котором эти силы неравны нулю.

Для устранения малой неуравновешенности, возникающей после изготовления звеньев и их монтажа из-за несоблюдения размеров в процессе изготовления, неточности сборки, неоднородности материала, звенья балансируют.

 

Условия уравновешенности ротора

Деталь, вращающаяся в опорах, называется ротором. В связи с появлением быстроходных машин возникла проблема уравновешивания быстровращающихся деталей. Так, например, скорость некоторых турбин, валов гироскопов, суперцентрифуг достигает 3-50 тысяч об/мин и малейшее смещение центра масс с геометрической оси вращения вызывает появление больших сил инерции, т.е. вибрационных явлений в машине и фундаменте.

При вращении какой-либо i-й массы m на нее действует сила инерции, которую можно разложить на нормальную   и тангенциальную   составляющие (рис. 6.1).

Величины этих сил можно вычислить по формулам

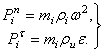                                                (1)

                                                Рис. 6.1. Схема ротора

 

Спроектируем эти силы на оси х, у, z и определим моменты этих сил относительно осей:

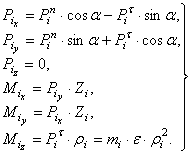                                    (2)

Подставив (1) в (2) и просуммировав, получим (учитывая, что  , )

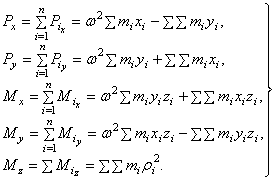
                                                         (3)

Последнее уравнение в (3) можно исключить, так как момент   не создает дополнительной реакции в опорах ротора.

Силы   и  , моменты   и   равны нулю в том случае, если координаты x и y массы m расположены на оси вращения z (т.е. центр масс ротора неподвижен):

                                                                                            (4)

Это есть условие статической уравновешенности ротора.

Моменты   и   равны нулю, если  центробежные моменты инерции ротора равны нулю:

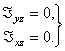                                                                                         (5)

Это есть условие динамической уравновешенности ротора.

Такое уравновешивание применяется для плоских деталей, длина которых мала по сравнению с диаметром.

Выводы: ротор статически уравновешен, если его центр тяжести расположен на оси вращения; ротор динамически уравновешен, если его ось вращения является главной центральной осью инерции.

Уравновешенность ротора можно охарактеризовать и силовыми параметрами. Он статически уравновешен, если главный вектор сил индукции  . Ротор динамически уравновешен, если главный вектор моментов сил инерции  .

При проектировании роторов используют условия (4) и (5). При проверке уравновешенности изготовленных роторов используют условия   и  . Устранение остаточной неуравновешенности уже изготовленного ротора, возникшей по причинам неточности изготовления, монтажа, из-за неоднородности материала, из которого изготовлен ротор, называется балансировкой. Балансировка вращающихся масс осуществляется на специальных балансировочных станках, при этом исключается неуравновешенность, вызванная неточностью изготовления детали.

 

Уравновешивание вращающихся масс

Уравновешивание масс, находящихся в одной плоскости

Положения отдельных неуравновешенных масс  , расположенных на роторе, можно охарактеризовать величинами радиус-векторов   относительно оси его вращения. Система вращающихся масс будет уравновешена, если главный вектор сил инерции, действующих на эти массы при их совместном вращении, равен нулю:

где   – сила инерции, действующая на i-ю массу;   – сила инерции уравновешивающей массы  , расположенной на расстоянии   от оси вращения ротора.

Сила инерции, действующая на i-ю массу, вращающуюся с постоянной скоростью  , равна  .

Рассмотрим систему, состоящую из трех неуравновешенных вращающихся масс m₁, m₂ и m₃ (рис. 6.2).

                                               а)                                                                                 б)

                        Рис. 6.2. Система неуравновешенных масс (а) и план сил инерции (б)

 

Условием уравновешенности данной системы масс является уравнение

.

Так как  , то это уравнение можно записать в виде

Так как   (мы рассматриваем вращающуюся систему масс), то

.                               (6)

Уравнение (6) можно решить аналитическим и графическим методами.

При аналитическом методе решения составляются уравнения проекций сил на координатные оси, из которых находят являющееся неизвестным последнее слагаемое.

Найдем   и   графическим методом, то есть построением векторного многоугольника (см. рис. 6.2, б), являющегося графической интерпретацией векторного уравнения (6). Предварительно выбираем масштаб сил

,

где z₁ – длина вектора, изображающего силу  , (мм).

Размерность масштаба   (если масса задана в кг, радиус – в м).

Переведем масштабом   другие известные слагаемые уравнения (6) в векторные отрезки:

Тогда векторное уравнение (6) запишется в виде

.

Построив векторный силовой многоугольник (см. рис. 6.2, б) в масштабе  , из него определим длину вектора  . Выбрав из конструктивных соображений величину  , вычисляем уравновешивающую массу

.

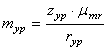Поместив ее на роторе в направлении вектора   на расстоянии от оси вращения, равном длине этого вектора, уравновесим ротор.

На практике наиболее часто статическое уравновешивание проводят:

- выбирая симметричные схемы механизма;

- устанавливая на звеньях механизма противовесы (или корректирующие массы);

- размещая противовесы на дополнительных звеньях или кинематических цепях.

 

Уравновешивание вращающихся масс, расположенных произвольно

Последовательность уравновешивания масс, расположенных произвольно, рассмотрим на примере ротора с системой четырех неуравновешенных масс (рис. 6.3). Пусть известны величины неуравновешенных масс   и их положения относительно оси вращения ротора, обусловленные радиусами – векторами   и расстояниями   относительно одной из произвольно выбранных плоскостей I, перпендикулярной оси вращения рассматриваемого ротора.

При вращении ротора и неуравновешенных масс с постоянной угловой скоростью на каждую из масс действует сила инерции

.

Так как угловая скорость в рассматриваемом здесь частном случае является величиной постоянной, то угловое ускорение отсутствует ( = 0) и тангенциальная составляющая силы инерции равна нулю.

                             а)                                                                     б)

                             в)                                                                                      г)

                Рис. 6.3. Уравновешивание масс, расположенных произвольно:

                а – вид на ротор с торца; б – вид на ротор с боку;

                в – план сил при статическом уравновешивании;

                г – план моментов сил при динамическом уравновешивании

 

Выбираем плоскости приведения I и II (см. рис. 6.3), в которых будем располагать уравновешивающие массы.

Задача заключается в том, что необходимо уравновесить массы динамически.

Сначала проводим статическое уравновешивание в плоскости I. Его последовательность описана в предыдущей главе.

,  ,

.                                                                             (7)

Используя (7), построим векторный многоугольник и графически найдем  .

Уравновесим действие инерционных моментов, т.е. выполним условие  . Для этого запишем уравнения

,    .       (8)

Так как  , то из уравнения (8) следует, что

.                                            (9)

Решая графически векторное уравнение (9), находим  .

Предварительно выбираем масштаб

.

Тогда уравнение (9) запишется в виде

.

При этом принимаем, что векторы моментов   повернуты на 90⁰ и совпадают с направлением  .

.                                                                       (10)

Находим из (10) величину  , задавшись  , или наоборот. Здесь   равна расстоянию между плоскостями приведения I и II.

Проводя от оси вращения ротора линию, параллельную  , откладываем на ней с противоположных сторон   и на концах этих векторов устанавливаем две уравновешивающие массы  . Причем одна из них будет расположена в плоскости I, другая – в плоскости II. Массы   и   в плоскости I можно объединить в одну массу.

 

Балансировка вращающихся масс (роторов)

Уравновешивание роторов или систем масс используется при проектировании механизмов.

В уже изготовленных роторах встречаются, как было сказано выше, неоднородности материала, возникают неточности изготовления и сборки, в результате чего возникает остаточная неуравновешенность, которую нужно устранять балансировкой.

Различают балансировку:

– статическую, которую производят для достаточно плоских роторов типа дисков, колес, маховиков, шкивов. Ротор при этом устанавливают в опорах с малым трением (например, на призмах) и путем добавления масс или высверливания добиваются безразличного положения балансируемогоротора на  опорах;

– динамическую, которую выполняют для роторов, имеющих значительную длину (валы, широкие колеса, шкивы и т.д.), на специальных станках.

Задача балансировки ротора заключается в определении, в выбранных плоскостях коррекции, значений и углов дисбалансов и размещении в этих плоскостях корректирующих масс, дисбалансы которых равны по величине и противоположны по направлению найденным дисбалансам ротора. На практике балансировку проводят: при конструировании - расчетными методами, в процессе изготовления деталей и узлов - экспериментально на специальных балансировочных станках. Балансировка на станках является более точным и надежным методом, по сравнению с расчетными. Поэтому она применяется для ответственных деталей с высокими рабочими частотами вращения. Корректировка масс ротора осуществляется либо присоединением к нему дополнительных корректирующих масс (наплавлением, наваркой или привинчиванием противовесов), либо удалением части массы ротора с “тяжелой” стороны (фрезерованием или высверливанием). Точность балансировки характеризуется величиной остаточного дисбаланса   ротора в каждой из плоскостей коррекции. Величина   не должна превышать допустимых для данного класса точности значений, регламентируемых ГОСТ 22061-76.

Балансировка эквивалентна уравновешиванию системы инерционных сил, прикладываемых к подвижному ротору для его равновесия. Эту систему, как и любую произвольную систему сил, можно заменить равнодействующими - главным вектором и главным моментом или двумя векторами, расположенными в произвольных параллельных плоскостях. Для уравновешивания системы сил достаточно уравновесить эти равнодействующие. При балансировке операции над силами заменяют действиями над дисбалансами. Поэтому для жестких роторов вышесказанное можно сформулировать так: жесткий ротор можно уравновесить двумя корректирующими массами, расположенными в двух произвольно выбранных плоскостях, перпендикулярных оси его вращения. Эти плоскости называют плоскостями коррекции.

 

Уравновешивание механизмов

Целью уравновешивания механизмов является устранение переменных во времени и пространстве воздействий стойки, станины механизма на опору, фундамент, вызывающих колебания фундамента и здания, а также уменьшение вибрации.

 

Условия уравновешенности механизма

Условия уравновешенности механизмов в общем виде можно охарактеризовать уравнениями

,

,

где   и   – главный вектор сил и главный момент сил давления станины механизма на фундамент, опору;   и   – главный вектор сил и главный момент всех других сил, внешних по отношению к механизму;   и   – главный вектор сил инерции и главный момент сил инерции звеньев механизма.

С достаточной для практики точностью часто ограничиваются условиями

,                                                                    (11)

.

Этого можно достичь установкой противовесов на подвижных звеньях, рациональным размещением центров масс звеньев механизма при его проектировании.

 

Статическое уравновешивание плоского механизма с помощью противовесов

Часто ограничиваются лишь статическим уравновешиванием механизма и его звеньев, т.е. выполнением условия (11)  . Это условие соответствует постоянству положения центров масс звеньев относительно стойки (т.е. центр их масс должен быть неподвижен). Так как  ,  , то необходимо обеспечить условие  , т.е. ускорение центра тяжести должно отсутствовать.

 

Рассмотрим последовательность статического уравновешивания на примере четырёхшарнирного механизма (рис. 6.4, а). Заменяем массы звеньев 1, 2, 3 сосредоточенными массами в точках A, B, C, D, причём в силу неподвижности точек A и D, массы, сосредоточенные в этих точках, можно не учитывать.

                                                                             Рис. 6.4

 

Приведённые массы в точках В и С равны:

;

.

Так как заменяющие массы   и   совершают вращательное движение, то для уравновешивания сил инерции необходимы противовесы с массами   и  , определяемыми из условий (рис. 6.4, б):

;                      ,

где, задавая длины противовесов, можно получить их массы и наоборот.

Рассмотрим моментное уравновешивание на примере четырёхшарнирного механизма. Его приближённое моментное уравновешивание можно осуществить после статического уравновешивания, введя в схему механизма два одинаковых дополнительных противовеса   (рис. 6.5), соединённых с зубчатыми колёсами “a” и “b”. Колесо “a” жёстко связано с кривошипом 1 и вращается с угловой  скоростью  , а равное ему колесо “b” вращается с той же угловой скоростью  , но угловые координаты противовесов отличаются на 180⁰, поэтому момент пары сил инерции от противовесов   равен  . Подбирая положение точки E, можно обеспечить направление  , противоположное направлению  , а массу противовесов   определяют из условия  .

                                           Рис.6.5

 

Уравновешивание роторов при проектировании

Статическое уравновешивание при проектировании

При проектировании статически уравновешивают детали, имеющие небольшие осевые размеры и конструктивно неуравновешенные, например, дисковые кулачки (рис. 6.6)

Когда кулачок неподвижен  , реакция в опоре  . При вращении кулачка, реакция в опоре равна векторной сумме сил тяжести и центробежной силы инерции

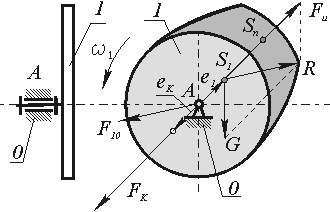
                                            Рис.6.6

 

При проектировании детали типа кулачка уравновешиваются так: в деталь с центром на оси вращения вписывается окружность, подсчитываются площади ограниченные контуром кулачка и расположенные вне или внутри окружности, определяется массы и центры масс   неуравновешенных частей кулачка, находится эксцентриситет   центра масс   кулачка по величине и направлению и определяется его дисбаланс с помощью корректирующей массы  , размещаемой на эксцентриситете  , создается дисбаланс   равный по величине и противоположный по направлению  .

 

Динамическое уравновешивание при проектировании

Динамическое уравновешивание при проектировании проводят с деталями и узлами, в которых массы распределены относительно оси вращения неравномерно, например, детали типа коленчатого вала. Эти детали делят на несколько дисков и в каждом диске, также как при статическом уравновешивании, определяют величину и направление дисбаланса  .

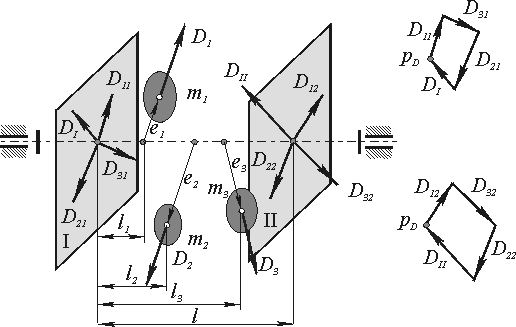
                                                                            Рис.6.7

 

На детали выбирают две плоскости коррекции и каждый вектор дисбаланса раскладывают на две составляющие, расположенные в плоскостях коррекции. Затем составляющие векторы дисбалансов в плоскостях коррекции суммируются и их равнодействующий дисбаланс, например,  , уравновешивается соответствующей корректирующей массой  . Пример такого уравновешивания изображен на рис. 6.7.

 

Статическое уравновешивание масс плоских рычажных механизмов (ме­тодом статического размещения масс).

Основная теорема плоского зацепления. Следствия.

Для постоянства передаточного отношения при зацеплении двух профилей зубьев необходимо, чтобы радиусы начальных окружностей зубчатых колёс, перекатывающихся друг по другу без скольжения, оставались неизменными. Если рассмотреть обращённое движение начальных окружностей, когда всей системе задана угловая скорость (  ), то второе колесо будет условно неподвижным и точка Р является мгновенным центром относительного вращения колёс (рис. 70,а). Эта точка, называемая полюсом зацепления, где контактируют начальные окружности, делит межцентровое расстояние на отрезки, обратно пропорциональные угловым скоростям, т. к.

.

Рассмотрим обращённое движение профилей зубьев зубчатых колёс (рис. 70, б).

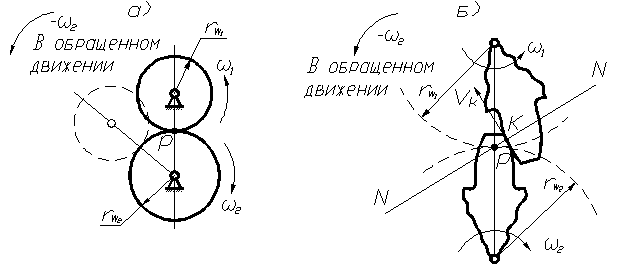
рис. 70

Точка контакта зубьев (точка к), принадлежащая первому колесу, вращается вокруг точки Р, которая будет мгновенным центром скоростей. Скорость   и совпадает с общей касательной к профилям в точке к при условии постоянства этого контакта.

рис. 71

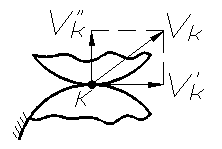В противном случае постоянного контакта не будет, так как появится составляющая   и профили разомкнутся (рис. 71). Так как рассматривается произвольное положение зубьев, то можно сформулировать теорему.

Нормаль NN к касающимся профилям зубьев, проведённая через точку их касания, делит межцентровое расстояние на части, обратно пропорциональные угловым скоростям.

Эта теорема, сформулированная Виллисом в 1841 г., определяет основной закон зацепления профилей, которые не могут быть произвольными, а должны быть специально подобраны.

Эвольвента окружности, ее уравнение и свойства.

Эвольвентой называется кривая, очерчиваемая точкой прямой, при перекатывании этой прямой по окружности без проскальзывания (рис. 1). В теории зацепления прямую называют производящей (образующей), а окружность – основной окружностью (радиус r_b).

Рассмотрим построение эвольвенты Е (рис. 1). В произвольной точке эвольвенты М проведем нормаль, которая касается основной окружности в точке В, получаем радиус кривизны эвольвенты ρ.

Из прямоугольного треугольника ΔОВМ найдем катет МВ:

 

Из условия образования эвольвенты радиус кривизны МВ должен быть равен длине развертываемой дуги АВ основной окружности: АВ = r_b (+),

 

где   полярный угол наклона радиус вектора;   угол между направлением радиус вектора и направлением радиуса основной окружности проведенного в точке касания нормали. Отсюда:

 

Разность тангенса и угла представляет собой эвольвентную функцию называемую инволютой. Инволюта является параметром для геометрических расчетов зубчатых механизмов.

Свойства эвольвенты:

        эвольвента не имеет точек внутри основной окружности;

        нормаль к любой точке эвольвенты направлена по касательной к основной окружности;

        центр кривизны эвольвенты лежит в точке касания нормали с основной окружностью.

Основные геометрические параметры зубчатых колес.