1.Механизм, машина, звено, стойка, входные и выходные звенья. Кинемати­ческие пары и их классификация. Кинематические цепи: плоские и про­странственные, замкнутые и незамкнутые.

Машина – это устройство, выполняющее механические движения для преобразования энергии, материалов или информации. Различают группы машин: 1. Энергетические (ДВС), 2. Технологические (станки, прессы). 3. Информационные (преобразование и переработка информации).

Механизм – это устройство, выполняющее преобразование движения одного или нескольких твердых тел в требуемое движение других твердых тел.

Звено – это одно или несколько жестко соединенных твердых тел, входящих в состав механизма. В каждом механизме имеется стойка (звено неподвижное или принимаемое за неподвижное). Звенья подразделяются на: неподвижные (стойка, неподв. направляющая) и подвижные (кривошип, шатун, коромысло, ползун, кулиса, кулачок). Входное звено – это звено, которому сообщается движение, преобразуемое механизмом в требуемое движение других звеньев. Выходное звено – это звено, совершающее движение, для выполнения которого предназначен механизм.

Кинематическая пара – это подвижное соединение двух соприкасающихся звеньев. По характеру соприкосновения звеньев различают низшие и высшие кинематические пары. Классификация кинематических пар:

1. по виду места контакта (места связи) поверхностей звеньев:

• низшие – в которых контакт звеньев осуществляется по плоскости или поверхности (пары скольжения);

• высшие – в которых контакт звеньев осуществляется по линиям или точкам (пары, допускающие скольжение с перекатыванием)

2. по относительному движению звеньев, образующих пару:

• вращательные;

• поступательные;

• винтовые;

• плоские;

• сферические.

3. по способу замыкания (обеспечения контакта звеньев пары):

• силовое – за счет действия сил веса или упругости пружины;

• геометрическое – за счет конструкции рабочих поверхностей пары.

4. по числу условий связи, накладываемых на относительное движение звеньев (число условий связи определяет класс кинематической пары);

5. по числу подвижностей в относительном движении звеньев.

Классификация КП по числу подвижностей и по числу связей приведена в таблице:

1. Кинематические цепи и их классификация.

Кинематическая цепь – это система звеньев, связанных между собой кинематическими парами. Любой механизм представляет собой кинематическую цепь (к. ц.) звеньев, соединенных в кинематические пары (к.п.). К. ц. могут быть простыми и сложными, открытыми и замкнутыми, плоскими и пространственными. В простой к. ц. каждое из ее звеньев входит в состав одной или двух к. п., а в сложной к. ц. имеются звенья, входящие в состав трех и более к. п. В открытой к. ц. имеются звенья, входящие в состав одной к. п., а в замкнутой цепи каждое звено входит в состав 2-х и более к. п. (рис.6,а-в). Если точки всех звеньев двигаются в одной или параллельных плоскостях, то к. ц. называется плоской, в противном случае к. ц. – пространственная (точки звеньев описывают плоские кривые в непараллельных плоскостях или пространственные кривые).

Число степеней свободы пространственных и плоских механизмов.

Плоский механизм – механизм, в котором все точки и звенья перемещаются в плоскостях параллельных между собой.

Пространственный механизм – механизм, в котором все точки и звенья перемещаются в плоскостях не параллельных между собой.

степени свободы — это совокупность независимых координат перемещения и/или вращения, полностью определяющая положение системы или тела.

Твёрдое тело, движущееся в трёхмерном пространстве, максимально может иметь шесть степеней свободы: три поступательных и три вращательных. Большинство обычных механизмов имеют одну степень свободы, то есть, имеется одно входное движение, определяющее одно выходное движение. Кроме того, большинство механизмов являются плоскими. W – число степеней свободы механизма. W=1 – для плоских механизмов; W ≠ 1 – для пространственных механизмов.

Определение числа степеней свободы механизма W=3*n-2*P5-P4 – формула Чебышева для плоских механизмов. W – число степеней свободы; n – число подвижных звеньев; Р5 – число пар 5-го класса механизма; Р4 – число пар 4-го класса механизма. Для плоских механизмов если W ≠ 1, то допущена ошибка, либо присутствуют звенья, создающие лишнюю степень свободы.

Число степеней свободы пространственного механизма:

Формула Сомова-Малышева:

p_i - число «i-й» подвижности.

Принцип Ассура образования плоских рычажных механизмов. Структур­ные группы и их классификация.

Ассуром Л.В. была предложена оригинальная структурная классификация. По этой классификации любой рычажный механизм не имеющий избыточных связей и местных подвижностей может быть образован путём присоединения к начальному (первичному) механизму групп звеньев с нулевой степенью подвижности (групп Ассура). Механизм = Начальный + Начальный + .... + Структурная + Структурная + ...

Группа Ассура классифицируются по числу к.п. которыми они присоеденены к основному механизму. Это число определяет порядок группы. Кроме того группа Ассура имеет класс определяемый числом к.п. образующий замкнутый контур. Под начальным механизмом понимают механизм, состоящий из двух звеньев (одно из которых неподвижное – стойка) образующих кинематическую пару с одной W_пм=1 или несколькими W_пм>1 подвижностями.

Структурной группой Ассура (или группой нулевой подвижности) называется кинематическая цепь, образованная только подвижными звеньями механизма, подвижность которой (на плоскости и в пространстве) равна нулю (W_гр = 0). Для плоских механизмов с низшими парами структурная формула групп Ассура имеет вид: W = 3•n-2•p5= 0 , откуда

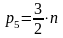
Поскольку в группе не может быть дробное число кинематических пар, то группы Ассура должны состоять только из четного числа звеньев (табл. 1)

Таблица 1

Класс и порядок группы Ассура	2кл. 2 пор.	3кл. 3 пор.	и т. д.
Число звеньев группы nгр	2	4
Число кинематических пар p5	3	6

Чтобы из механизма выделить группы Ассура, необходимо помнить их основные признаки, вытекающие из определения:

• число звеньев в группе должно быть четным (n = 2, 4, 6 и т.д);

• степень подвижности группы всегда равна нулю; степень подвижности оставшейся части механизма при отсоединении групп Ассура не должна изменяться.

Группа Ассура, классификация групп Ассура (класс, порядок и вид групп II класса).

Группой Ассура называется кинематическая цепь, которая в случае ее присоединения элементами внешних пар к стойке получает нулевую степень подвижности, т.е. образует ферму. Группа Ассура характеризуется классом, порядком и видом.

Класс группы Ассура определяется максимальным классом контура входящего в группу. Класс контура – наибольшее число кинематических пар образующих в группе замкнутый контур. Если группа Ассура образована двумя звеньями ей в качестве исключения присваивается 2-й класс.

Порядок группы Ассура определяется числом кинематических пар, которыми она присоединяется к основному механизму.

Вид группы Ассура (её характеристика) определяется соотношением входящих в неё вращательных и поступательных кинематических пар. Поводком называется звено, входящее в группе в две кинематические пары, одна из которых свободная и служит для присоединения к одному из подвижных звеньев механизма или к стойке. Порядок структурных групп определяется числом поводков.

Механизмы классифицируются по степени сложности групп, входящих в их состав. Класс и порядок механизма определяется классом и порядком наиболее сложной из входящих в него групп. Особенность структурных групп Ассура - их статическая определимость. Если группу Ассура свободными элементами звеньев присоединить к стойке, то образуется статически определимая конструкция. Используя группы Ассура удобно проводить структурный, кинематический и силовой анализ механизмов. Наиболее широко применяются простые рычажные механизмы, состоящие из групп Ассура 2-го класса 2-го порядка.

6а

Число разновидностей таких групп для плоских механизмов с низшими парами невелико, их всего пять (см. рис. 1 б, в, г, д, е)

Рисунок 1.

Кинематический анализ плоских рычажных механизмов графическим ме­тодом.

Кинематический анализ механизма – исследование его основных параметров с целью изучения законов изменения и на основе этого выбор из ряда известных наилучшего механизма. Кинематический анализ механизма выполняется либо для заданного момента времени, либо для заданного положения входного звена; иногда для анализируемого положения механизма задают взаимное расположение каких-либо его звеньев.

Цели:

1. Определение кинематических характеристик звеньев: перемещение; скорость; ускорение; траектория движения; функция положения при известных законах движения входных (ведущих) звеньев.

2. Оценка кинематических условий работы рабочего (выходного) звена.

3. Определение необходимых численных данных для проведения силового, динамического, энергетического и других расчётов механизма.

Исходные данные:

1. Кинематическая схема механизма.

2. Размеры и иные геометрические параметры звеньев (но только такие, которые не изменяются при движении механизма).

3. Законы движения входных звеньев (или параметры движения, например, угловая скорость и угловое ускорение входного звена в выбранном для анализа положении механизма).

Для механизмов, подчиняющихся классификации Л. В. Ассура, порядок кинематического анализа определяется формулой строения: вначале находят параметры движения начальных механизмов и затем – структурных групп в порядке следования их в формуле строения. Здесь следует руководствоваться простым правилом: кинематика любого элемента формулы строения может быть изучена только после того, как она изучена для всех предшествующих в этой формуле элементов.

Задачи:

- о положениях звеньев механизма. Определение траекторий движения точек;

- о скоростях звеньев или отдельных точек механизма;

- об ускорениях звеньев или отдельных точек механизма.

Методы:

- графический (или метод графиков и диаграмм);

- графоаналитический (или метод планов скоростей и ускорений);

- аналитический;

- экспериментальный.

 

Графический метод кинематического анализа

Преимущество этого метода заключается в наглядности и простоте. Он хорош для кинематического анализа звеньев, совершающих возвратно-поступательное движение. Недостаток метода – невысокая точность, которая зависит от точности графических построений.

Задача о положениях решается построением нескольких совмещённых планов механизма в выбранном масштабе длин при различных последовательных положениях ведущего звена.

Задачи о скоростях и ускорениях решаются построением графиков (диаграмм) перемещений, скоростей и ускорений исследуемой точки.

Последовательность кинематического анализа:

1. Сначала строят несколько (чаще всего 12 и более) совмещенных планов механизма в произвольно выбранном масштабе длин.

2. Затем строят график пути (перемещения) исследуемой точки или звена, для чего используют совмещённые планы механизма и последовательные положения на них исследуемой точки или звена.

3. Графическим дифференцированием графика перемещений строят график скорости исследуемой точки.

4. Графическим дифференцированием графика скоростей строят график ускорений.

Графическое дифференцирование можно производить методом хорд и методом касательных. С целью повышения точности удобно использовать оба метода одновременно.

 

Кинематический анализ плоских рычажных механизмов аналитическим методом.

Графический (метод диаграмм) и графоаналитический методы (метод планов скоростей и ускорений) кинематического анализа механизмов имеют недостатки: невысокая точность, определяемая точностью графических построений, и большая трудоёмкость. При иcпользовании графического метода необходимо построить диаграммы перемещений, скоростей и ускорений для каждой исследуемой точки механизма, а при использовании графоаналитического метода – несколько планов скоростей и ускорений механизма, чтобы определить динамику изменения скорости и ускорения интересующих нас точек (т.е. при различных положениях механизма).

Эти недостатки отсутствуют в аналитическом методе. Но при этом необходимо составлять достаточно сложные аналитические зависимости (формулы) и иметь возможность решать их с использованием компьютерных техники и технологии, что в последнее время возможно и доступно.

Методы аналитического исследования:

метод замкнутых векторных контуров (метод Зиновьева) удобен для кинематического анализа практически всех используемых в технике несложных рычажных механизмов;

метод преобразования координат (метод Морошкина) удобен для кинематического анализа многозвенных механизмов типа манипуляторов промышленных роботов.