2.3 Определение касательных напряжений при простом изгибе крыла

Рис. 7 К определению касательных напряжений при простом изгибе

Для любого участка i,i+1 сечения крыла касательное усилие при простом изгибе находится по формуле

,

где - касательное усилие на участке i, i+1 сечения в предположении, что в

точках j = 1,2,... касательные усилия равны нулю (каждая из этих точек

служит началом отсчета дуг для соответствующего контура);

- вспомогательные функции, Рис.8.

Рис.8 Вспомогательные единичные функции

Неизвестные усилия в точках 1,2,3 определяются из системы уравнений

, ,

где ;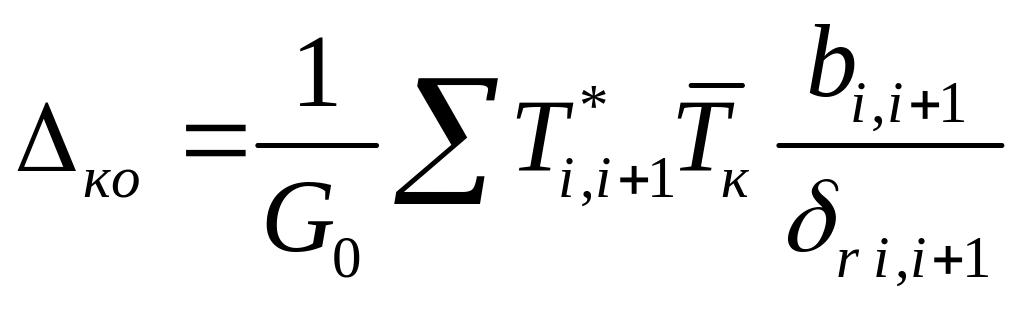

;

.

- редукционный коэффициент обшивки и стенок при работе на сдвиг

;

Для обшивки принимаем , для стенок лонжеронов .

Усилия вычисляются по формуле

.

Значения момента инерции приведенного сечения относительно главной оси и, редуцированных площадей элементов продольного набора, расстояний от оси и до центров тяжести редуцированных площадей элементов берутся по результатам последнего приближения расчета нормальных напряжений.

Доля перерезывающей силы, воспринимаемой обшивкой и стенками лонжеронов крыла, равна

,

,

где - число элементов продольного набора в сечении крыла;

- угол между осью i-го элемента продольного набора и плоскостью хорд.

Результаты расчета касательных напряжений при простом изгибе сведены в таблицу 9.

Эпюры погонных касательных сил приведены на Рис.9.

Проверка правильности построения

для эпюры

, , ,

, , ;

для эпюры

, , ,

, , ;

, , , .

Таблица 9. Расчет касательных сил при простом изгибе

Таблица 9. (Продолжение)

Таблица 9. (Продолжение)

Таблица 9. (Продолжение)

Таблица 9. (Продолжение)

Рис.9 Эпюры касательных сил при простом изгибе

2.6 Определение координат центра жесткости сечения

Координату центра жесткости в центральной системе координат u, v можно определить по формуле

.

В центральной системе координат координата центра жесткости .

Относительно носка профиля координата центра жесткости , .

Относительная координата центра жесткости , .

2.7 Определение крутящего момента относительно центра жесткости сечения крыла

Крутящий момент относительно оси жесткости крыла возникает от нормальных к хорде составляющих погонной воздушной нагрузки , от массовых сил крыла , от массовых сил топлива и агрегатов , расположенных в крыле.

Рис.10 Определение крутящего момента

Погонный крутящий момент в любом сечении определится равенством

,

где - координата центра жесткости относительно носка профиля;

- координата центра давления относительно носка профиля.

При построении линии центров масс принимаем .

Методом численного интегрирования получим крутящий момент в сечении относительно центра жесткости

,

где - сосредоточенный момент от агрегата.

Для стреловидного крыла .

Результаты расчета крутящего момента сведены в таблицу 10.

Эпюры погонного и крутящего момента представлены на Рис.11 и Рис.12.

Таблица 10. Расчет крутящего момента

Рис.11 Эпюра погонного крутящего момента

Рис. 12 Эпюра крутящего момента

2.8 Определение касательных напряжений при свободном кручении крыла

Для определения погонных касательных усилий, возникающих при свободном кручении крыла, имеем следующую систему уравнений

,

,

,

,

где - относительный угол закручивания сечения крыла;

- удвоенная площадь i-го контура;

- высота j-ой стенки лонжерона;

- редуцированная толщина j-ой стенки лонжерона.

Решая эту систему, получаем

, , , .

Зная значения погонных касательных сил построим их эпюру – Рис.13

Суммарные значения касательных усилий в сечении крыла получим, складывая ранее найденные касательные усилия от простого изгиба с усилиями от кручения

.

Эпюра суммарных усилий представлена на Рис.14.

Результаты расчета сведены в таблицу 11.

Таблица 11. Касательные усилия от кручения крыла и результирующие усилия

Рис.13 Касательные силы при свободном кручении крыла

Рис. 14 Результирующие касательные силы от изгиба и кручения