контрольные, зачеты / Перелік розписових питань МКР_1

Перелік питань, які виносяться на модульну контрольну роботу №1 з дисципліни «Вища математика»

1. Приріст аргументу і приріст функції. Означення похідної, її механічний і геометричний зміст.

Якщо змінна величина х змінила своє значення від х₀ до х₁, то різниця між її новим значенням і початковим називається приростом аргументу і позначається символом ∆х. Таким чином, ∆х = х₁ - х₀, звідки випливає, що х₁ = х₀ + ∆х. Початкове значення аргументу х₀ одержало приріст ∆х. Внаслідок цього значення функції зміниться на величину f(х1) - f(х0). Ця різниця називається приростом функції в точці х0, відповідним до приросту ∆х, і позначається символом ∆у.

Похідною функції у = f(х) у точці х₀ називається границя відношення приросту функції в точці х₀ до приросту аргументу, коли приріст аргументу прямує до нуля.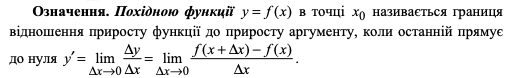 Механічний зміст похідної: Похідна характеризує швидкість зміни функції при зміні аргументу. S = S (t) – залежність пройденого шляху від часу V = S ′(t) – швидкість прямолінійного руху a = v′(t) – прискорення прямолінійного руху. Похідна за часом є мірою швидкості зміни відповідної функції. Миттєва швидкість v нерівномірного прямолінійного руху є похідна функції, яка виражає залежність пройденого шляху s від часу t.

Геометричний зміст похідної: Кутовий коефіцієнт дотичної до графіка функції у = f(x), що приведена у точці цього графіка з абсцисою х₀ дорівнює похідній функції у = f(x) у цій точці, тобто k = f '(x₀).

2. Диференційовність функції. Похідні деяких основних елементарних функцій. Основні правила диференціювання.

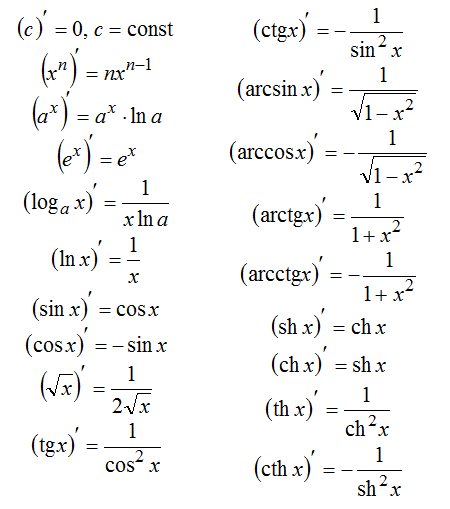
Якщо функція f(х) диференційована в точці х₀, то вона неперервна в цій точці. Якщо функція f(х) диференційована на проміжку (тобто в кожній його точці), то вона неперервна на цьому проміжку.

3. Похідна оберненої функції. Похідні обернених тригонометричних функцій. Похідна складної функції.

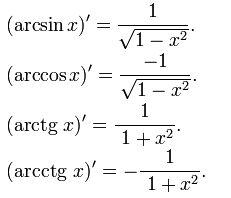
Складеною функцією називають функцію від функції. Якщо змінна y є функцією від u: y = f(u), а u в свою чергу – функцією від x; u = ϕ(x), то y є складеною функцією від x, тобто y = f(ϕ (x)).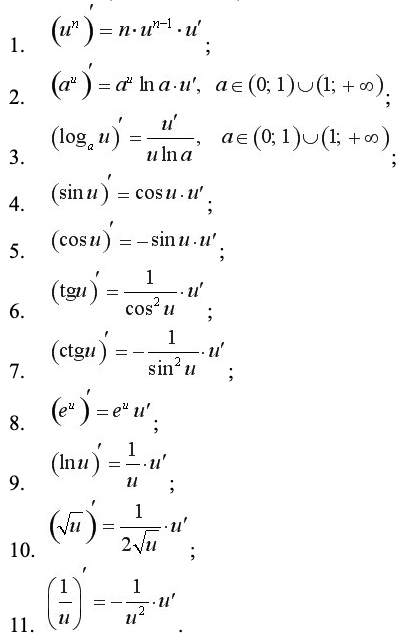

4. Неявна функція і її похідна. Похідна функції, заданої параметрично. Таблиця похідних. Похідні вищих порядків.

Функції, в яких незалежна змінна x і функція y зв'язані між собою формулою f(x,y)=0 з якої не можна відокремити саму функцію називаються неявною функцією від аргумента x. Однак саму похідну від функції по змінній x можна обчислити. Для цього диференціюють функцію f(x,y) по x, при цьому враховують, що сама функція залежна від змінної y=y(x). З одержаного рівняння згруповують доданки, що містяться при похідній y' і виражають її.

Під похідною вищих порядків розуміють подальше диференціювання функції, то одержимо похідну другого порядку, або другу похідну функції y=f(x), і вона позначається:

Похідна третього порядку матиме запис:

5. Диференціал функції та його геометричний зміст. Зв‘язок диференціала з похідною.

Диференціал наближено дорівнює приросту функції і пропорційний приросту аргументу. Диференціал функції f (х) при заданих значеннях х і ∆х дорівнює приросту ординати дотичної до кривої у = f (х) в точці х. Приріст функції y при цьому дорівнює приросту ординати кривої. Таким чином, заміна приросту функції на її диференціал геометрично означає заміну ординати АР кривої ординатою дотичної. Геометричний зміст диференціала: PN =y, QN = MNtg=хf'(x) = f'(x)dx = dy.

6. Диференціал складної функції. Інваріантність форми диференціала 1-го порядку.

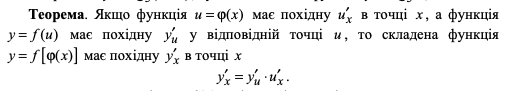
Диференціал функції визначають однією і тою самою формулою незалежно від того, чи є її аргумент незалежною змінною, чи є функцією іншого аргументу. Цю властивість диференціала звуть інваріантністю форми першого диференціала.

7. Диференціали вищих порядків.

Нехай функція y = f (x) диференційована в кожній точці деякого проміжку. Її диференціал першого порядку dy =f ′(x)dx є функцією двох змінних: аргументу і диференціала. Нехай також диференційована в кожній точці деякого проміжку. Будемо розглядати у виразі диференціал як постійний множник. Тоді

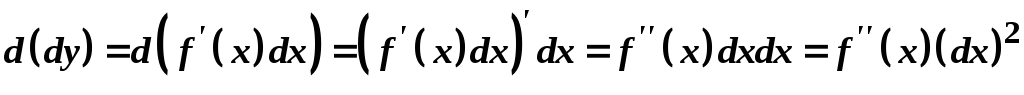
Диференціал d(dy) називається диференціалом другого порядку і позначається як d²y. Отже,

8. Деякі теореми диференціального числення. Теореми Ферма і Ролля.

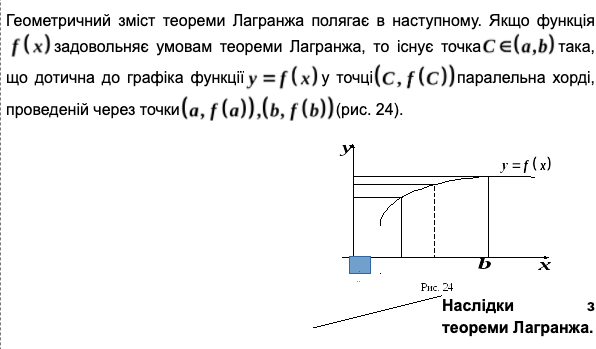
9. Деякі теореми диференціального числення. Теореми Лагранжа і Коші, їх застосування.

10. Правила Лопіталя. Формула Тейлора із залишковим членом у формах Лагранжа та Пеано.

11. Необхідні і достатні умови зростання і спадання функцій.

• Якщо диференційована функція зростає на деякому проміжку, то похідна цієї функції невід’ємна на цьому проміжку.

• Якщо диференційована функція спадає на деякому проміжку, то похідна цієї функції не додатна на цьому проміжку.

12. Максимум і мінімум функції. Необхідна умова екстремуму. Достатня умова екстремуму.

Точка x₀ називається точкою локального максимуму (або мінімуму) функції y=f(x), якщо існує такий окіл 0<|x-x₀|<delta цієї точки, який належить області визначення функції, і для всіх аргументів x<x₀ з цього околу виконується нерівність f(x)<f(x₀) (або f(x)>f(x₀)).

Точки максимуму і мінімуму називаються точками екстремуму функції , а значення функції в екстремальних точках – її екстремальними значеннями.Нехай функція y=f(x) неперервна в деякому інтервалі, що містить критичну точку x₀, і диференційована у всіх точках цього інтервалу (за винятком, можливо, самої точки x₀). Тоді для точки x₀ функція має максимум, якщо для аргументів x<x₀ виконується f'(x₀)>0, а для x>x₀ умова f'(x₀)<0.

Якщо ж для x<x₀ похідна менша нуля f'(x₀)<0 , а для x>x₀ більша нуля f'(x₀)>0, то для точки x=x₀ функція має мінімум.

Таким чином, функція на відрізку [a, b] досягає свого найбільшого значення на одному з кінців цього проміжку або в такій точці його, яка є точкою максимуму. Аналогічне твердження можна сформулювати й про найменше значення функції: воно досягається на одному з кінців даного проміжку або в такій внутрішній точці, яка є точкою мінімуму.

13. Знаходження найбільшого і найменшого значень функції, диференційованої на відрізку.

Найбільший з максимумів і найменший з мінімумів називають найбільшим і найменшим значенням функції на відрізку.

Схема знаходження найбільшого і найменшого значень функції на проміжку така:

• Знайдіть похідну функції і її критичні точки;

• Знайдіть значення функції на кінцях проміжку;

• Знайдіть значення функції в критичних точках, які належать заданому проміжку;

• З усіх знайдених значень функції оберіть найбільше і найменше.

Неперервна на відрізку [a;b] функція y=f(x) набуває своїх найбільшого та найменшого значень, або в критичних точках (у точках, в яких похідна перетворюється в нуль чи не існує), що належать досліджуваному проміжку, або на його кінцях x=a, x=b.

14. Поняття опуклості і вгнутості графіка функцій. Достатні умови.

Крива y=f(x) називається опуклою на інтервалі, якщо всі її точки, крім точки дотику, лежать нижче її дотичної на цьому інтервалі.

Крива y=f(x) називається увігнутою на інтервалі, якщо всі її точки, крім точки дотику, лежать вище її дотичної на цьому інтервалі.

15. Точки перегину. Необхідна умова точки перегину.

16. Поняття вертикальної асимптоти та їх визначення.

Пряма l називається асимптотою кривої, якщо відстань δ від змінної точки кривої до цієї прямої прямує до нуля, коли точка M , рухаючись по прямій, віддаляється в нескінченність.

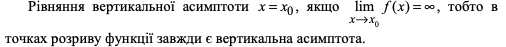
17. Означення похилої асимптоти. Необхідна та достатня умова похилої асимптоти. Приклади.

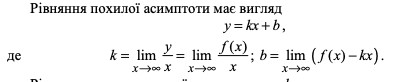
18. Загальна схема досліджень функцій і побудови їх графіка.

1. Визначаємо область допустимих значень (ОДЗ).

2. Виявляємо, чи є функція парною або непарною, періодичною тощо.

3. Знаходимо точки екстремуму та інтервали монотонності.

4. Знаходимо точки перегину та інтервали опуклості.

5. Знаходимо рівняння асимптот графіка функції (якщо вони є).