2. Формула Стирлинга

Изучение эйлеровских интегралов завершаем важ­ной для приложений формулой Стирлинга, дающей приближенное значение для гамма-функции или для функции при больших значениях аргумента.

Теорема (формула Стирлинга). При имеет место равенство:

,

где , а для величины остатка R выполняются неравенства

.

Отметим, что если воспользоваться соотношением

,

то из теоремы 1 можно получить еще один вариант формулы Стирлинга вида:

.

В частности, при отсюда имеем

Следовательно, справедлива асимптотическая формула

,

которая также называется формулой Стирлинга. Более тщательные вычисления позволяют получить оценку вида для остатка R в асимптотической формуле теоремы. Этот результат был установлен Гауссом. Он же доказал, что величину в асимптотической формуле для можно заменить на , где .

ЛЕКЦИЯ 12

Евклидово пространство интегрируемых функций. Ортонормированная система. Задача о наилучшем приближении элемента евклидова пространства по ортонормированной системе. Базисность и замкнутость ортонормированной системы. Ряд и коэффициенты Фурье. Неравенство Бесселя и равенство Парсеваля

1. Евклидово пространство интегрируемых функций

Пусть линейное пространство интегрируемых по Риману на отрезке [a, b] функций. В нём можно определить скалярное произведение: удовлетворяющее следующим аксиомам скалярного произведения:

1. (нулевая функция – функция, принимающая нулевые значения в точках непрерывности и возможно положительные значения в точках разрыва, мера которых равна нулю, т.е. нулевая функция – это не одна, а целый класс функций).

2. 

3. 

4. 

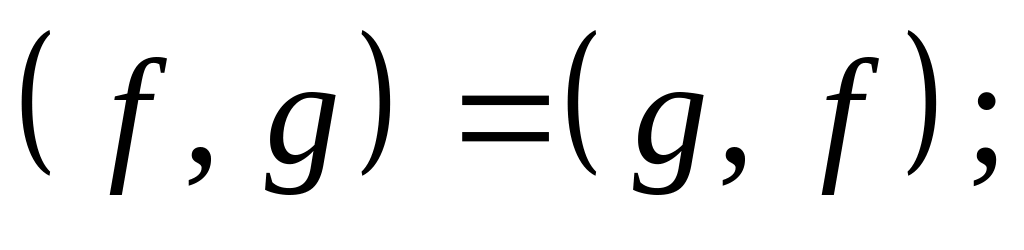
Линейное пространство со скалярным произведением называется Евклидовым пространством. Евклидово пространство можно рассматривать как нормированное, в котором норма определяется по правилам: Для такого отображения выполнены все аксиомы нормы:

1. 

2. 

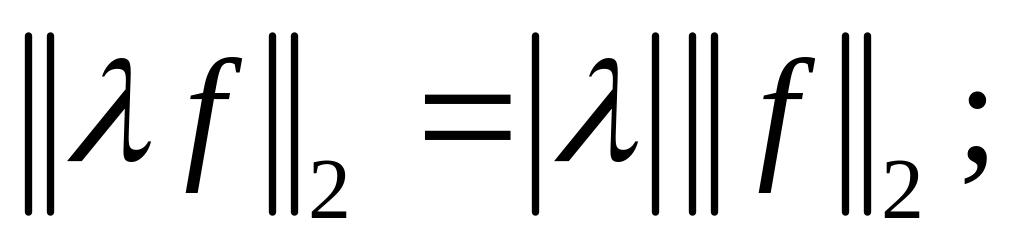
3. неравенство треугольника, и оно легко выводится из неравенства Коши-Буняковского

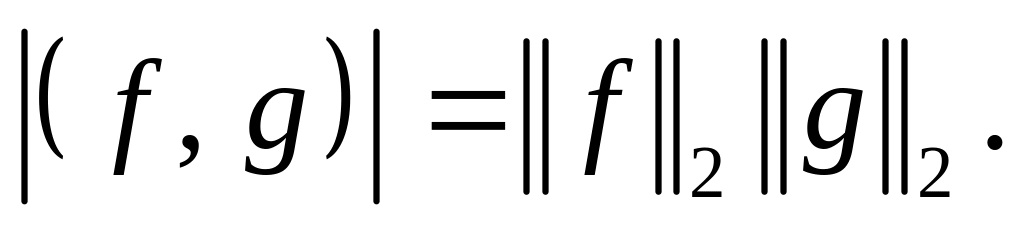
В свою очередь неравенство Коши-Буняковского позволяет определить и угол между функциями: В частности, Норма позволяет определить расстояние между функциями и сходимость последовательности функций: Такую сходимость называют среднеквадратичной сходимостью

Сравним равномерную сходимость и среднеквадратичную сходимости на отрезке [a, b]. Из равномерной сходимости вытекает среднеквадратичная сходимость:

Обратное неверно.

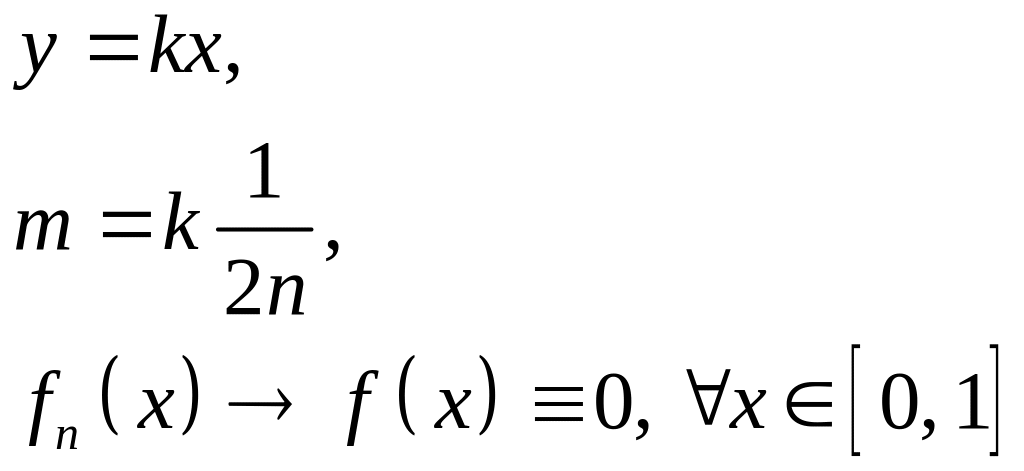
равномерной сходимости нет.

Пространство является бесконечномерным. В нём линейно-независимую систему, например, образуют функции (система степеней).

Задача. Охарактеризовать мощность пространства

2. Ортонормированная система. Задача о наилучшем приближении элемента евклидова пространства по ортонормированной системе

Счётная система функций называется ортогональной, если и ортонормированной, если система ортогональная и нормированная, т.е. . Далее будем обозначать ОС – ортогональная система, ОНС – ортонормированная система.

Рассмотрим задачу о наилучшем среднеквадратичном приближении функции по ОНС.

Пусть ОНС. Линейные комбинации вида будем называть полиномами порядка n по этой ОНС. Множество всех таких полиномов порядка n будет образовывать линейное подпространство размерности п, т.е. , с базисом

Задача. Доказать, что ОНС – линейно-независимая система.

Для величина называется величиной наилучшего среднеквадратичного приближения функции f полиномами порядка п по нашей ОНС. Полином называется полиномом наилучшего среднеквадратичного приближения

Теорема. причём

Доказательство. ОНС,

Итак, единственен.

Доказано.