Лекция 3 Равномерная сходимость и интегрируемость предельной функции функциональной последовательности и суммы функционального ряда

1. Равномерная сходимость и интегрируемость предельной функции функциональной последовательности

Теорема 2. Если

Доказательство. Будем пользоваться следующим критерием интегрируемости функции по Риману (критерий Римана):

Пусть произвольное разбиение, тогда:

Итак,

Опять а из

Это и означает справедливость второй части теоремы 2.

Доказано.

2. Равномерная сходимость и интегрируемость суммы функционального ряда

Теорема 2. Если , и функциональный ряд сходится к то

Доказательство. Если По теореме 2 (по теореме 2) =

Доказано.

Лекция 4 Равномерная сходимость и дифференцируемость предельной функции функциональной последовательности и суммы функционального ряда. Пространство . Его полнота

1. Равномерная сходимость и дифференцируемость предельной функции функциональной последовательности

Теорема 3. Если

1. 

2. 

3. 

то также равномерно сходится к

.

Доказательство. Будем пользоваться следующими критерием:

произвольное, а

Далее пользуясь критерием Коши, покажем равномерную сходимость последовательности

равномерно по

Далее:

Доказано.

2. Равномерная сходимость и дифференцируемость суммы

функционального ряда

Теорема 3. Если

1. 

2. 

3. 

Доказательство. Если то

2. 

3. 

Доказано.

3. Пространство . Его полнота

Пространство - это множество раз непрерывно дифференцируемых на отрезке функций. Это линейное пространство, в котором можно ввести норму

Охарактеризуем сходимость в этом пространстве:

т.е. сходимость по норме пространства эквивалентна равномерной сходимости самой последовательности и последовательности её производных до порядка k включительно.

Отметим, что пространство также является полным.

Лекция 5 Степенные ряды. Поточечная сходимость. Радиус и интервал поточечной сходимости. Формула Коши-Адамара

1. Степенные ряды. Поточечная сходимость

Степенным рядом называется ряд вида коэффициенты степенного ряда,

Нашей основной задачей будет исследование области поточечной сходимости, равномерной сходимости и свойств суммы (1).

2. Радиус и интервал поточечной сходимости. Формула Коши-Адамара

Положительное число называется радиусом сходимости ряда (1), если при ряд (1) сходится, а при Интервал называется интервалом сходимости.

Теорема 1(об области поточечной сходимости). Любой ряд вида (1) имеет радиус сходимости Точнее:

1. если то область сходимости

2. если

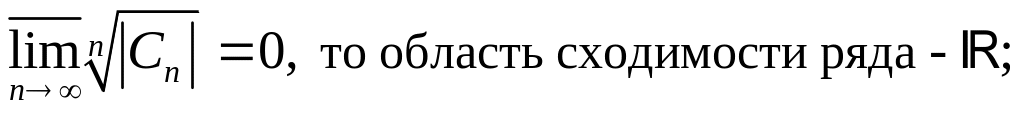
3. если то при ряд (1) сходится, а при ряд (1) - расходится, причём в интервале сходимости ряд (1) будет сходиться абсолютно.

Доказательство. При доказательстве будем использовать радикальный признак Коши в следующей форме:

1. если то ряд (2) сходится;

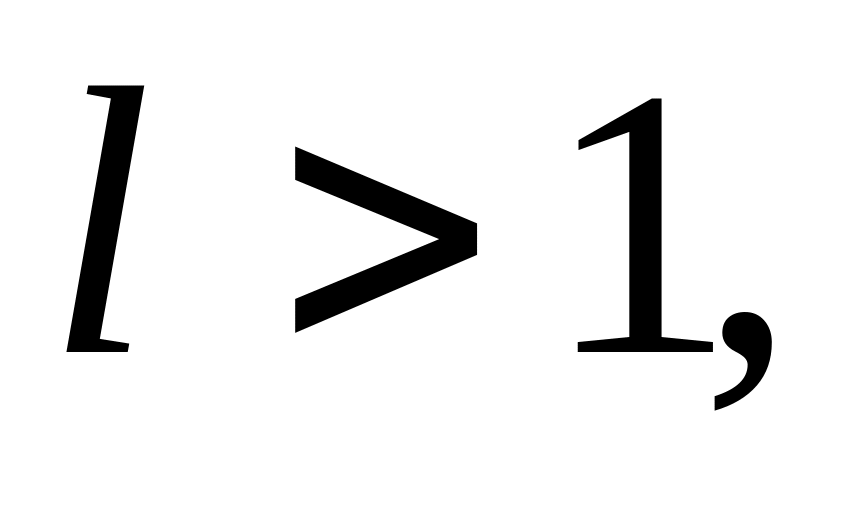2. если то ряд (2) расходится и

Исследуем абсолютную сходимость ряда (1):

1. 

2. сходится абсолютно.

Доказано.

Пример. Исследовать сходимость ряда

Исследуем абсолютную сходимость ряда.

Итак, область абсолютной сходимости - область сходимости ряда -