Министерство сельского хозяйства Российской федерации

ФГОУ ВПО «Белгородская государственная сельскохозяйственная академия»

ПРАКТИКУМ

ПО ФИЗИКЕ

ДЛЯ СТУДЕНТОВ АГРОНОМИЧЕСКОГО ФАКУЛЬТЕТА

Белгород 2009

Удк 53(075.8)

ББК 22.3 я73

А П69

Практикум по физике. Для студентов агрономического факультета. Составители: ст. Преподаватель Акупиян а.Н., ассистент Шаршанова м.А. - Белгород, 2009 - Изд-во БелГсха.- 58с.

Рецензент – А.В. Сабылинский, канд. физ.-мат. наук, доцент кафедры физики БелГТУ им. Шухова.

© Белгородская государственная сельхозакадемия, 2009

Содержание:

1	ЛАБОРАТОРНАЯ РАБОТА ДИНАМИКА ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ	4
2	ЛАБОРАТОРНАЯ РАБОТА МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ	19
3	ЛАБОРАТОРНАЯ РАБОТА ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ ТВЕРДЫХ ТЕЛ	25
4	ЛАБОРАТОРНАЯ РАБОТА ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЯЗКОСТИ ЖИДКОСТИ	35
5	ЛАБОРАТОРНАЯ РАБОТА ДИФФУЗИЯ В ГАЗАХ	44
6	ЛАБОРАТОРНАЯ РАБОТА МАГНИТНОЕ ПОЛЕ	50

Лабораторная работа динамика поступательного движения

Цель работы: Изучение законов динамики поступательного движения тел и их экспериментальная проверка с помощью машины Атвуда.

Приборы и

принадлежности: Лабораторный комплекс ЛКМ-4, набор грузов, линейка.

Краткая теория

Простейшая форма движения – механическое движение.

Механическое движение – изменение взаимного расположения тел или их частей друг относительно друга в пространстве с течением времени.

Время – характеризует последовательность и длительность со­бытий.

Пространство – характеризует расположение материальных объектов друг отно­сительно друга и их протяженность.

По характеру решаемых задач механику условно разделяют на статику, кинематику и динамику.

Статика – учение о равновесии тел.

Кинематика – раздел механики, изучающий движение тел без учета масс тел и причин движения.

Динамика – учение о движении тел под действием сил. Классическая механика рассматривает макроскопические тела и их движение со скоростями, много меньшими скорости света. При больших скоростях переходят к теории относительности, а при исс­ледовании микрочастиц – квантовой механике.

При малых скоростях и больших массах уравнения теории относительности переходят в уравнения классической механики.

Для описания механического движения надо выбрать тело (сис­тему тел), относительно которого нужно рассматривать движение исследуемого тела. Кроме того, нужно выбрать способ измерения времени, например часы. Все это называется системой отсчета.

Система отсчета – система координат, жестко связанная с телом отсчета, и выбранный способ измерения времени (часы).

Тело отсчета – тело (система тел), принимаемое в данном слу­чае за неподвижное, относительно которого рассматривается движе­ние других тел.

Начало отсчета – точка на теле отсчета, относительно которой определяется положение других тел (точка 0 на рис.1).

Радиус-вектор точки М₀ – направ­ленный отрезок прямой, вектор, соединяющий начало отсчета О с точкой М.

Координаты х, y, z точки М – расстоя­ния от начала координат О до про­екции точки М на оси координат (рис.2).

Материальная точка – любое тело, размерами и формой которого можно пренебречь по сравнению с размера­ми других тел, по сравнению с расстояниями до них.

Траектория – линия, описываемая в пространстве движущимся телом, например след лыж на снегу.

Путь L – расстояние, пройденное телом вдоль траектории (скалярная величина).

Перемещение – вектор, соединяющий начальное (точка М ) и ко­нечное

(точка М) положения тела (рис.1). При прямолинейном движении путь и величина перемещения совпадают.

При движении точки в пространстве ее координаты с течением вре­мени t изменяются. Эта зависимость координат от времени может быть задана в виде уравнений: х = х(t); y = y(t); z = z(t) или , называемых кинематическими уравнениями движения.

В зависимости от формы траектории различают прямолинейное и криволинейное движения точки.

Для характеристики быстроты движения вводится понятие ско­рости. Средняя скорость показывает, чему равно перемещение тела за единицу времени (за 1 с): .

Другими словами: есть отношение перемещения ко времени этого перемещения.

Равномерным называют такое движение, при котором за любые равные промежутки времени тело проходит одинаковые пути (т.е. движение с постоянной скоростью, без ускорения). При неравномерном движении скорость от точки к точке траек­тории меняется. Скорость тела в данный момент времени в данной точке траектории называют мгновенной скоростью.

или . (1)

Вектор направлен по касательной к траектории.

Движение тела, при котором его скорость за любые равные про­межутки времени изменяется одинаково, называется равнопеременным или равноускоренным. Равнопеременное движение - частный случай неравномерного движения.

Ускорением тела при его равнопеременном движении называ­ют величину, равную отношению изменения скорости тела к про­межутку времени t, за который это изменение произошло

, (2)

где – скорость в начальный момент времени t = 0, или начальная скорость;

– скорость тела к моменту времени t.

Равнопеременное движение – это движение с постоянным ускоре­нием ( ).

Если а > 0, то движение называется равноускоренным, при а < 0 – равнозамедленным. В общем случае ускорение может быть средним и мгновенным.

, . (3)

Основные кинематические уравнения равнопеременного поступа­тельного движения:

*для пути при прямолинейном движении , (4)

*для скорости , (5)

*для связи между ними . (6)

При соответственно имеем : a t; .

Частным случаем равноускоренного движения является свободное падение тел под действием силы тяжести с ускорением, равным ускорению сво­бодного падения .

Движение по окружности – частный случай криволинейного дви­жения. Скорость тела в любой точке криволинейной траектории направлена по касательной к ней. Скорость при этом, как вектор, может изменяться и по модулю (величине), и по направле­нию. Если модуль скорости остается неизменным, то говорят о равномерном криволинейном движении.

Пусть тело в виде материальной точки движется по окружности радиуса R из точки 1 в точку 2. При этом точка за время пройдет путь L_1,2 , равный длине дуги окружности между точками 1 и 2 (рис.3)

За это же время t радиус – вектор , проведенный из центра ок­ружности О к точке, повернется на угол Вектор скорости в точке 2 отличается от на величину ∆ :

∆ = – . (7)

Для характе­ристики изменения скорости на величину ∆ (т.е. по направлению к модулю) введем среднее ускорение , совпадающее с вектором ∆ .

= . (8)

Мгновенное ускорение _мгн в соответствии с выражением (3) нам потребуется при неравномерном движении по окружности. При равномерном движении _мгн и совпадают.

Разложим на перпендикулярные составляющие и . Одна составляющая пусть будет совпадать с направлением ско­рости в точке 2 и будет перпендикулярна радиусу окружности R, проведенному из О к этой точке. Вторая составляющая тогда будет перпендикулярна скорости в точке 2 и соответственно будет совпадать с направлением радиуса окружности R, проведенно­му из О к этой точке 2.

– тангенциальная составляющая ускорения направ­лена по касательной в любой точке траектории, т.е. совпадает с направлением вектора скорости в этой точке и определяет его изменение по величине.

– нормальная (перпендикулярная) составляющая ус­корения с одной стороны направлена перпендикулярно вектору , а с другой – направлена к центру окружности О, она определяет изме­нение вектора скорости в этой точке по направлению.

– называют еще центростремительным ускорением, т.к. оно направлено к центру окружности R.

Связь и по правилу сложения векторов может быть записана:

.

При движении материальной точки по окружности радиус - век­тор , проведенный из центра окружности О к точке, поворачивает­ся на угол Δφ (рис.3). Для характеристики вращения вводятся понятия угловой скорости ω и углового ускорения .

Угол φ можно измерять в радианах. 1 рад. равен углу, кото­рый опирается на дугу L, равную радиусу R окружности, т.е.:

если L₁₂ = R. (11)

Продифференцируем уравнение (11):

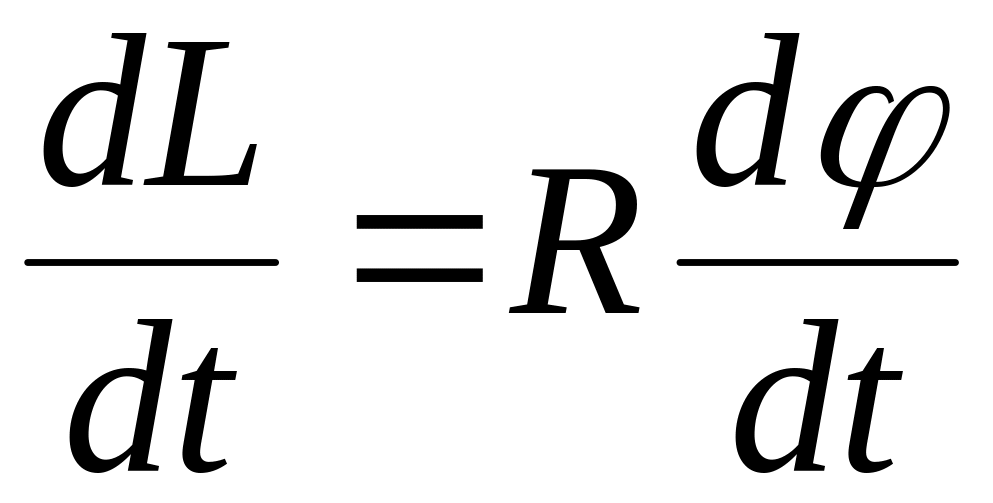. (12)

Величина . Величину называют угловой ско­ростью (измеряется в рад/с). Переписав (12), получим связь между линейной и угловой скоростями:

= ω R. (13)

Величина ω векторная.

Направление вектора определяется правилом правоходового винта (буравчика): оно совпадает с направлением переме­щения винта, ориентированного вдоль оси вращения тела и вращае­мого в направлении вращения тела.

Мгновенным угловым ускорением называется векторная величина, опреде­ленная как производная от угловой скорости:

. (14)

Вектор совпадает с осью вращения и направлен в ту же сто­рону, что и вектор , если вращение ускоренное, и в – противо­положную, если вращение замедленное.

Число оборотов тела в единицу времени (в 1с) называют час­тотой вращения.

Время Т одного оборота тела называют периодом вращения. При этом R опишет угол Δφ = 2π радиан

С учетом сказанного

. (15)

Используя (8) и (13), уравнение (14) в скалярной форме можно записать следующим образом:

(16)

Тогда тангенциальное ускорение:

(17)

Нормальное ускорение а_n можно выразить следующим образом.

(18)

Для вращательного движения с постоянным угловым ускорением можно записать уравнение кинематики по аналогии с уравнениями (4)

(19)

(20)

Динамика рассматривает законы движения тел и причины появле­ния ускорения. В основе динамики лежат законы Ньютона, понятия силы, массы, импульса.

Физическое содержание первого закона было раскрыто Галилеем до Ньютона. Считалось, что телам при движении присуще внутреннее свойство останавливаться. Галилей установил, что это свойство обусловлено не внутренними, а внешними причинами. Например, если уменьшить силу трения, то и скорость движущегося тела будет изме­няться меньше. Очевидно, если внешнее воздействие удалось бы свести к нулю, то тело стало бы двигаться с постоянной скоростью (равномерно) и прямолинейно или покоиться.

Первый закон динамики гласит: всякое тело сохраняет состоя­ние покоя или равномерного прямолинейного движения до тех пор, пока внешнее воздействие не заставит его изменить это состояние.

Условиями, при которых тело покоится или движется равномерно и прямолинейно, могут быть следующие:

1) на тело не действуют другие тела (одинокое тело во Вселе­нной) – реально не существуют;

2) действие других тел компенсируется (это реально).

Свойство тел сохранять состояние покоя или равномерного пря­молинейного движения называется инерцией. Поэтому первый закон Ньютона называют еще законом инерции.

Первый закон Ньютона выполняется не во всякой системе отсче­та. Те системы, в которых он выполняется, называются инерциаль­ными системами отсчета. Инерциальной может быть система, связан­ная со свободно движущимся в пространстве телом. Реально в при­роде нет свободных, не взаимодействующих ни с чем, тел. Поэтому, строго говоря, нет и инерциальных систем. Но существуют мно­жество реальных систем, которые с большей степенью точности приближаются к инерциальным. Такой системой может служить гелио­центрическая (звездная) система отсчета (начало координат в центре Солнца, а оси направлены на звезды). В меньшей степени инерциальной системой можно считать Землю (Земля испытывает ус­корение, обусловленное суточным вращением вокруг оси и годичным движением вокруг Солнца). Поэтому первый закон Ньютона на Земле выполняется приближенно. Однако для описания целого ряда движений этого оказывается достаточно.

Введем понятие массы. Массой тела называют физическую величину, являющуюся мерой его инерционных и гравитационных свойств. Попробуем остановить железнодорожный вагон и тележку носильщика, которые движутся с одинаковыми скоростями. Эффект окажется разным за счет отличия масс, следовательно, инерционных свойств. У вагона масса больше, чем у тележки, больше проявляется его инертность.

Сила тяжести, с которой тело вследствие притяжения к Земле давит на горизонтальную опору в пустоте вблизи Земли, называется весом тела F_в. Вес тела определяет его гравитационные свойства.

Вес тела принято определять формулой:

F_в= m·g, (21)

где m – гравитационная масса;

g – коэффициент пропорциональности, называемый ускорением свободного падения.

Отношение масс двух тел равно отношению их сил тяжести . На этом основано сравнение масс тел с помощью рычажных весов.

Произведение массы тела на его скорость Ньютон назвал количеством движения тела:

. (22)

принято в настоящее время называть импульсом тела.

Из выражения (22) и (3) следует:

и . (23)

Тогда с учетом выражения (23) можно записать

. (24)

Таким образом, получим второй закон Ньютона, который формулируется так: первая производная по времени от импульса тела равна действующей на нее силе. Вторая формулировка произведение массы тела на его ускорение равно силе, действующей на тело.

При криволинейном движении тело приобретает нормальное уско­рение (18) под действием силы F_n , направленной к центру кривизны траектории и поэтому называется центростремительной си­лой:

. (25)

Если на тело одновременно действуют несколько сил: , то нужно по правилу векторного сложения найти их результирую­щую а затем ускорение .

В системе СИ за единицу массы принят 1 кг. За единицу силы – 1Н (один ньютон) – т.е. сила, которая сообщает телу массой 1 кг ускорение 1 м/с² :

1Н = 1кг 1м/с² = 1кг м с^-2.

Измерить силу можно пружинным динамометром.

Плотность вещества тела равна массе в единице объема:

ρ = . (26)

Измеряется плотность ρ в кг/м³.

Представим себе двух конькобежцев, которые, стоя на льду, взялись за руки и попытались приблизить друг друга. Оба придут в движение, но с разными ускорениями и по величине и по направле­нию, если их массы m₁≠ m₂, причем

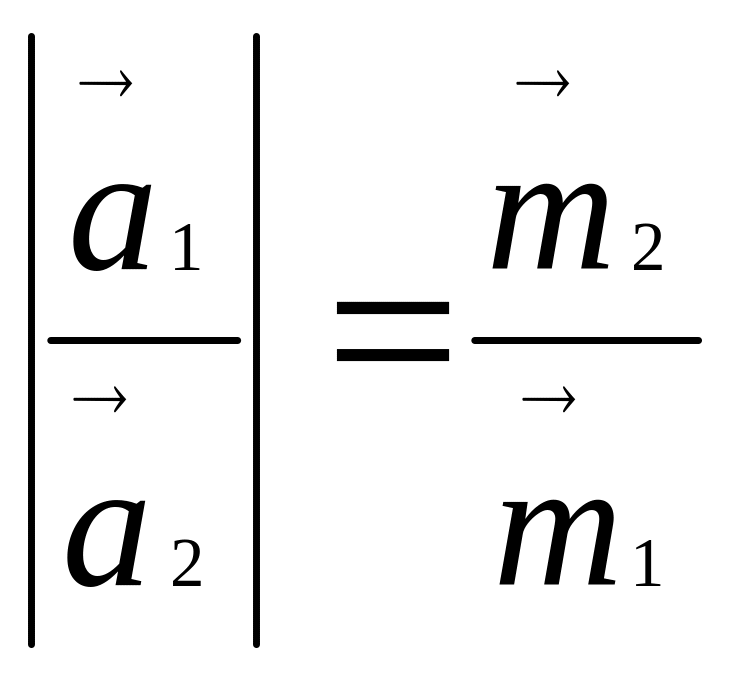или (28)

откуда m₁ = - m₂ или с учетом (24)

. (29)

Тела действуют друг на друга с силами, направленными вдоль одной прямой, равными по абсолютным значениям и противоположными по направлению - третий закон Ньютона.

При этом силы , приложены к разным телам и поэтому не могут компенсировать друг друга.

Машина Атвуда предназначена для изучения законов движения. Она состоит из двух грузов, связанных между собой нитью, переброшенной через блок, укрепленный на оси (рис. 4).

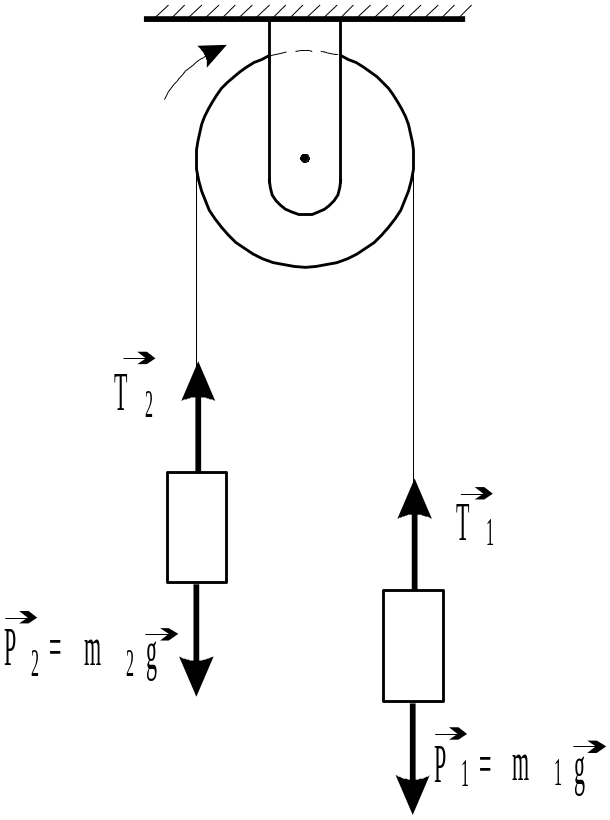
Рис.4

При рассмотрении системы необходимо различать два вида движения, в котором участвуют ее элементы: поступательное движение грузов и вращательное – блока.

При вращательном движении абсолютно твердого тела все точки его описывают окружности с центрами, лежащими на оси вращения.

Если пренебречь моментом инерции и трением в блоке, то ускоряющая сила F = P₁ – P₂, или по второму закону Ньютона, F = (m₁ + m₂)·a,

где и – массы гирь. Тогда:

. (30)

На рис.5 представлен внешний вид лабораторного комплекса ЛКМ – 4.

В своем составе он имеет:

1.	Каркас с ящиками.
1.2.	Вспомогательные стойки.
1.3.	Ножки каркаса.
3.1	Стойка большая комбинированная.
3.1.а.	Штыри с отверстиями для закрепления пружин.
3.2.	Шкив двустворчатый.
3.3.	Шкала.
4.	Измерительная система.
4.1.	Окно для подключения датчиков.
6.	Ящик для хранения инструментов.

Рис. 5. Лабораторный комплекс ЛКМ-4