1.3 Характеристика оригінального програмного забезпечення визначення пропускної здатності системи гнпс – прилегла ділянка нафтопроводу

Для визначення пропускної здатності системи ГНПС – прилегла ділянка нафтопроводу була використана стандартизована програма під назвою «Propuskna zdatnist», текст якої представлений у додатку .

Дана програма складається із двох блоків:

• розрахунок фізичних властивостей;

• розрахунок пропускної здатності.

У блоці «Розрахунок фізичних властивостей» відбувається розрахунок густини і кінематичного коефіцієнта в’язкості за температури грунту на глибині укладання нафтопроводу для умов місяця.

У блоці «Розрахунок пропускної здатності» відбувається розрахунок пропускної здатності методом послідовних наближень за алгоритмом, який наведений у пункті 1.2. Після знаходження пропускної здатності, дана програма розраховує потужність, яку споживають насосні агрегати.

Також дана програма розраховує пропускну здатність при різній кількості працюючих основних насосів.

1.4 Математичне моделювання фізичних властивостей нафти та характеристик насосів

В процесі транспортування нафти виникають задачі розрахунку їх властивостей. Основні фізико-хімічні властивості нафти, що впливають на технологію транспортування, густина і кінематичний коефіцієнт в’язкості.

Густина і кінематичний коефіцієнт в’язкості нафти залежать від температури. Оскільки температура нафти в трубопроводі за рахунок теплообміну із довкіллям у неізотермічних нафтопроводах стає рівною температурі середовища, у якому прокладено трубопровід, то необхідно провести розрахунок густини і кінематичного коефіцієнта в’язкості за середньомісячних температурах ґрунту на глибині укладання нафтопроводу.

Густину нафти за температури перекачування рахуємо за формулою

(1.29)

де - густина нафти за температури , кг/м³; - густина нафти за температури 20 ⁰С, кг/м³; 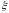- температурна поправка, кг/(м3 ⁰С), яка визначається за формулою

(1.30)

Кінематичний коефіцієнт в’язкості рідини за розрахункової температури визначаємо за формулою Рейнольдса-Філонова

(1.31)

де 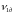- дослідне значення кінематичного коефіцієнта в’язкості нафти за температури ; - коефіцієнт крутизни віскограми, який визначається за формулою

(1.32)

де 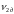- дослідне значення кінематичного коефіцієнта в’язкості нафти за температури .

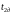Проведемо розрахунок густини і кінематичного коефіцієнта в’язкості нафти за мінімальної середньомісячної температури ґрунту на глибині укладання нафтопроводу, тобто для місяця березня з температурою ґрунту .

Визначаємо за формулою (1.30) температурну поправку

Визначаємо густину нафти за температури перекачування за допомогою формули (1.29)

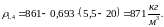
Визначаємо коефіцієнт крутизни віскограми за формулою (1.32)

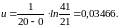
Кінематичний коефіцієнт в’язкості нафти за розрахункової температури визначаємо за формулою (1.31)

Аналогічно проводимо розрахунки густини і кінематичного коефіцієнта в’язкості для 12 місяців, за допомогою програми, текст якої наведено в додатку . Результати даних розрахунків наведено в таблиці 1.3.

Таблиця 1.3 – Результати розрахунку густини і кінематичного коефіцієнта в’язкості за температури перекачування для 12 місяців

Місяць	1	2	3	4	5	6	7	8	9	10	11	12
Густина, кг/м3	870,1	870,3	871,0	869,3	866,3	863,6	861,3	860,2	860,9	863,1	865,8	868,6
В’язкість, сСт	33,2	33,4	34,7	31,8	27,4	23,9	21,4	20,1	20,9	23,4	26,8	30,6

Згідно з даними таблиці 1.3 будуємо графічні залежності густини та кінематичного коефіцієнта в’язкості нафти від температури і місяця року. Дані графічні залежності представлені на рисунках 1.2 – 1.3.

Кожен насос має технічну і графічну характеристики, що наводяться в його паспорті. Технічна характеристика містить номінальні параметри роботи, тобто параметри, що відповідають режиму роботи при максимальному ККД.

У процесі експлуатації трубопроводу насоси можуть працювати при різних режимах. Тому виникає практична необхідність визначення напору, ККД, потужності та інших параметрів для будь-якого значення подачі. Це завдання вирішується з допомогою графічних характеристик насосів або їх математичних моделей.

Характеристика насоса – це графічна залежність основних параметрів роботи насоса ( напору, потужності, ККД, допустимого кавітаційного запасу) від його подачі при постійній частоті обертання і певних фізичних властивостях рідини на вході в насос.

З метою створення розрахункових алгоритмів і програмного забезпечення для проведення технологічних розрахунків режимів роботи трубопроводів графічні характеристики насосів доцільно описати математичними моделями. З достатньою для практичних розрахунків точністю робоча зона напірної характеристики нафтових насосів описується такою математичною моделлю

(1.33)

де і 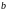- коефіцієнти математичної моделі.

Дані коефіцієнти можуть бути обчислені за координатами двох точок напірної характеристики насоса

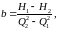(1.34)

(1.35)

де 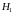, - напір насоса при подачі 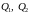відповідно.

Оскільки в даній роботі буде використовуватись насоси типу НМ 2500-230 зі змінним ротором на 0,5 і НПВ 2500-80, то графічні характеристики даних насосів наведені в додатку .

Координати точок знятих з напірної характеристики насосів для знаходження коефіцієнтів математичної моделі представлені у таблиці 1.4.

Таблиця 1.4 – Координати точок

Подача		Напір, м
м3/год	м3/с		НМ 2500-230	НПВ 2500-80
1000	0,2778		230	-
1750	0,486		200	-
1200	0,333		-	100
2600	0,722		-	78

Проведемо розрахунок коефіцієнтів математичної моделі для насоса типу НМ 2500-230 зі змінним ротом на 0,5.

За формулами (1.34) і (1.35) знаходимо коефіцієнти і

Отже, математична модель для насоса типу НМ 2500-230 зі змінним ротором на 0,5 набуде вигляду

(1.36)

Аналогічно проведемо розрахунок коефіцієнтів математичної моделі і для насоса типу НПВ 2500-80.

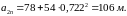
Отже, математична модель для насоса типу НПВ 2500-80 набуде вигляду

(1.37)

Робоча зона енергетичної характеристики насоса (кривої ККД) може бути описана такою математичною моделлю

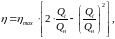(1.38)

де - максимальне значення ККД насоса, що відповідає його номінальній подачі .