Содержание
Лист
Содержание 1
Введение 1
1 Оптимизация системы 2
2 Характеристики скорректированной системы 5
3 Модель системы в пространстве состояний 8
4 Исследование системы на управляемость и наблюдаемость. 10
5 Цифровая модель САУ 12
6 Корреляционная функция между входом и выходом объекта. 15
Заключение 20
Литература 21
Введение
Моделирование [4] – это замена объекта (оригинала) и фиксация и изучение его свойств путем исследования модели.
Процесс моделирования [4] может быть разбит на следующие этапы:
1. Формулировка цели моделирования;
2. Разработка концептуальной модели;
3. Подготовка исходных данных;
4. Разработка математической модели;
5. Выбор метода моделирования;
6. Выбор средств моделирования;
7. Разработка программной модели;
8. Проверка адекватности и корректировка модели;
9. Планирование машинных экспериментов;
10. Моделирование;
11. Анализ результатов моделирования.
В ходе курсовой работы необходимо смоделировать систему управления приводом робота-манипулятора. Целью моделирования является создание эффективной, адекватной модели. При первом рассмотрении системы можно заметить следующее:
На вход системы поступает угол поворота, который, скорее всего, создается механическим усилием;
Этот сигнал с учетом ошибки преобразуется в электрическое напряжение;
Сигнал усиливается, корректируется и направляется на двигатель;
Выходной сигнал двигателя поступает на объект – робот-манипулятор.
В качестве средства моделирования будем использовать среду Matlab 6.5.0.1. Matlab обладает мощным встроенным языком и прочими средствами для создания эффективной модели системы.
1 Оптимизация системы
Необходимо подобрать параметры корректирующих устройств и коэффициент усиления электронного усилителя такими, чтобы выходной сигнал удовлетворял следующим показателям качества:
максимальное перерегулирование – не более 1%;
время нарастания – не более 1с;
длительность переходного процесса – не более 3с.
Модель
системы, созданная при помощи Simulink,
представлена на рис 1.
Рисунок 1 - Модель САУ
Для определения параметров проведём оптимизацию системы при помощи блока NCD OutPort. Начальные значения параметров придаются 1. Настройка параметров показана на рис. 2.
Рисунок 2 - Настройка параметров оптимизации
Задавать требования к переходному процессу можно непосредственно в окне блока NCD OutPort, передвигая красные линии, или ввести их значения в окне Step Response, как на рис. 3.
Рисунок 3 - Настройка характеристик переходного процесса
Приступаем к процессу оптимизации, нажав кнопку Start. Ход оптимизации показан на рис. 4, кривой зелёного цвета соответствуют оптимальные значения настраиваемых параметров.
Рисунок 4 - Процесс оптимизации системы
Полученные оптимизированные значения параметров:
2 Характеристики скорректированной системы
Переходная функция системы, полученная с помощью LTI Viewer, изображена на рис. 5.
Рисунок 5 - Переходная функция системы
Как следует из графика, время нарастания составляет 0.77с, длительность переходного процесса – 3с, величина перерегулирования равно 0.79%, то есть полученная система удовлетворяет предоставленным параметрам качества.
Для получения передаточной функции разомкнутой системы управления воспользуемся правилом преобразования структурных схем. Ход преобразования показан на рис. 6.
Рисунок 6 - Преобразование системы
Таким образом, полученная в результате преобразования передаточная функция имеет вид:
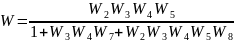
Для получения ПФ средствами Matlab воспользуемся функцией linmod, которая имеет следующие параметры:
‘sys’ – имя Simulink системы, из которой должна быть извлечена линейная модель;
x и u – начальный и конечный вектора соответственно. По умолчанию – 0;
Ts – постоянная времени для дискретной линеаризованной модели.
В зависимости от вида используемых параметров функция linmod может выдавать различные характеристики системы. В виде [num,den]=linmod('m2') выдает передаточную функцию системы. Полученная после некоторых математических преобразований передаточная функция:
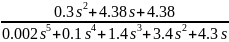
Построим фазовые амплитудные частотные характеристики разомкнутой системы, чтобы определить её запасы устойчивости, с помощью LTI Viewer в Simulink.
Рисунок 7 - АЧХ, ФЧХ и АФХ разомкнутой системы
Как показывают графики, запас устойчивости по амплитуде составляет 20.5 дБ, запас устойчивости по фазе – 51.1о.
3 Модель системы в пространстве состояний
Для случая линейной системы с p входами, q выходами и n переменными состояния описание имеет вид:
Где x— вектор состояния, элементы которого называются состояниями системы, y— вектор выхода, u— вектор управления, A — матрица системы, B— матрица управления, C— матрица выхода и D— матрица прямой связи.
Как известно, любой передаточной функции можно поставить в соответствие дифференциальное уравнение вида:
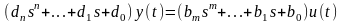
Выбор переменных состояния в принципе произволен и определяется зачастую исключительно удобством вычислений, поэтому введем следующие обозначения:
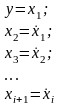
где i изменяется до n-1, тогда получим следующие уравнения
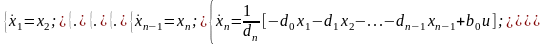
Из этой системы получим матрицы для описания системы в пространстве состояний.
В Matlab для получения матриц пространства состояния используется функция tf2ss, которая записывается в виде: [A,B,C,D]=tf2ss(num,den)
Получаем матрицы следующего вида:
A =
-0.0001 -0.0033 -0.1733 -3.9403 -9.6332 -6.6908 0
1 0 0 0 0 0 0
0 1 0 0 0 0 0
0 0 1 0 0 0 0
0 0 0 1 0 0 0
0 0 0 0 1 0 0
0 0 0 0 0 1 0
B =
1
0
0
0
0
0
0
C =
1.0e+007 *
0.0000 -0.0000 -0.0000 -0.0000 0.0625 5.7901 5.7901
D =
0