Аксиоматическое построение геометрии (аксиоматика Вейля и школьного курса геометрии). Логические основы изучения геометрии в 7-9 классах.
Аксиоматика Вейля.
Основные объекты – база структуры.
Имеем
три множества: 1)Е
,
элементы которой точки; 2)векторное
трехмерное пространствоV3;
3)множество полей действительных чисел
.
Основные поля:
1)основные объекты: Е, V,
2)основные отношения:
-
-
-
Система аксиом Вейля.
1.
2.
3.
3.1
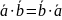
3.2
3.3
3.4
- скалярный квадрат,
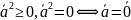
Множество Е называется 3-хмерным вещественным Евклидовым пространством, если выполнены все три аксиомы.
Замечание. Аксиомы 1-2 опр-т аффинное 3-хмерное пространство.
Теорема. Система аксиом 1-3 Вейля непротиворечива, если непротиворечива арифметика вещественных чисел.
Аксиоматика школьного курса геометрии.
По учебнику Атанасяна.
Основные понятия:
1)основные объекты: точка, прямая, плоскость.
2) основные отношения: принадлежность, лежать между, наложение.
Система аксиом:
1 группа. Аксиома принадлежности или связи.
.
Какова бы не была прямая а, существует хотя бы одна точка, которая ей не принадлежит.
Через любые две точки можно провести одну прямую, притом только одну.
2 группа. Аксиома взаимного расположения (А-В-С)
2.1
Для любых трех точек А,В,С
одна и только одна из них лежит между
ними.
2.2 любая точка прямой делит её на две части (на 2 класса)
2.3. любая прямая разбивает плоскость на 2 части.
3 группа. Аксиома равенства (наложения)
Определение. Фигуры F1 и F2 называются равными, если при наложении они совмещаются.
3.1
каков бы не был отрезок АВ и каков бы не
был луч А’Т. На луче от его начала можно
наложить отрезок A’B’
равный данному и только один (на луче
[А’Т)
).
3.2 каким бы не был луч для любого угла hk и любого луча. От начала данного луча заданного полуплоскость можно отложить угол h’k’ равный данному углу и только один.
3.3 если угол hk=углу h’k’, то при наложении их можно совместить 2-мя путями: 1)h=h’, k=k’; 2)h=k’, k=h’.
3.4
любая фигура=самой себе (
)
3.5 если F1=F2 следовательно F2=F1
3.6 если F1=F2 и F2=F3 следовательно F1=F3
4 группа. Аксиома меры (вводится понятие длины отрезка)
4.1 при выборе единичного отрезка е любому отрезку АВ ставится соответствующее положительное число – длина данного отрезка.
4.2
при данном выборе единичного отрезка
е
для любого числа а>0,
,
существует
отрезок АВ: длина отрезка АВ=а.
Замечание. В отношении меры углов в аксиоматике сказано, что мера углов вводится аналогичным образом.
4.3 какой бы не был угол hk на промежутке от 0 до (от 0 до 1800), каждому углу ставится в соответствии число .
4.4
.
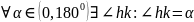4.5
АВ=АС+СВ.
4.6
5
группа. Аксиома
параллельности:
Система аксиом по Погорелову.
Основные понятия:
1)основные объекты: точка, прямая, плоскость.
2) основные отношения: принадлежность, лежать между, длина, мера угла.
1 группа. Аксиома принадлежности или связи.
для любого а существуют точки принадлежащие этой прямой и не принадлежащие ей.
Через любые две точки можно провести одну прямую и притом только одну.
2 группа. Аксиома взаимного расположения (А-В-С).
2.1
для любых трех точек АВС
.
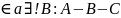2.2 любая прямая делит плоскость на 2 части.
3 группа. Аксиома меры.
3.1
(длина=числу)
3.2 Каждый угол имеет определенную градусную меру, большую нуля. Развернутый угол равен 1800. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
4 группа. Аксиома равенства.
Опр-е. отрезок АВ=отрезку CD, если длина АВ=длине CD.
Опр-е. угол hk=euke h’k’, если градусная мера угла hk=градусной мере h’k’.
4.1
на данном луче можно отложить от начала
отрезок равный данному, притом только
один.
4.2
,
на этом луче заданную полуплоскость
можно отложить угол
.
4.3
на луче от его начала заданную полуплоскость
можно отложить треугольник
.
5
группа.
Аксиома параллельности: Через любую
точку
можно провести неболее
одной
прямой
.
Логические основы изучения геометрии в 7-9 классах.
Цели изучения геометрии в 7 -9 класса:
в направлении личностного развития:
-развитие личностного и критического мышления, культуры речи;
- воспитание качеств личности, обеспечивающих, уважение к истине и критического отношения к собственным и чужим суждениям;
- формирование качеств мышления, необходимых для адаптации в современном информационном обществе;
- развитие интереса к математическому творчеству и математических способностей.
в метапредметном направлении:
-формирование представлений об идеях и о методах математики как об универсальном языке науки и техники, части общечеловеческой культуры;
-умение видеть математическую задачу в окружающем мире, использовать математические средства наглядности (рисунки, чертежи, схемы) для иллюстрации, интерпретации, аргументации;
- овладение умением логически обосновывать то, что многие зависимости, обнаруженные путем рассмотрения отдельных частных случаев, имеют общее значение и распространяются на все фигуры определенного вида, и, кроме того, вырабатывать потребность в логическом обосновании зависимостей.
в предметном направлении:
-выявление практической значимости науки, ее многообразных приложений в смежных дисциплинах и повседневной деятельности людей;
-создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.
Задачи курса геометрии 7- 9 класс класса:
– формирование мотивации изучения геометрии, готовности и способности учащихся к саморазвитию, личностному самоопределению, построению индивидуальной траектории в изучении предмета;
– формирование у учащихся способности к организации своей учебной деятельности посредством освоения личностных, познавательных, регулятивных и коммуникативных универсальных учебных действий;
– формирование специфических для геометрии стилей мышления, необходимых для полноценного функционирования в современном обществе, в частности, логического, алгоритмического и эвристического;
– формирование умений представлять информацию в зависимости от поставленных задач в виде таблицы, схемы, графика, диаграммы, использовать компьютерные программы, Интернет при ее обработке;
– овладение учащимися математическим языком и аппаратом как средством описания и исследования явлений окружающего мира;
– овладение системой математических знаний, умений и навыков, необходимых для решения задач повседневной жизни, изучения смежных дисциплин и продолжения образования;
– формирование научного мировоззрения;
– воспитание отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.