Теория вероятностей и математическая статистика

34. На плоскости начерчены две концентрические окружности, радиусы которых 5 и 10 см соответственно. Найти вероятность того, что точка, брошенная наудачу в большой круг, попадет также и в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в плоскую фигуру пропорциональна площади этой фигуры и не зависит от ее расположения.

А={попадание точки в кольцо, образованное построенными окружностями}

Согласно геометрическому определению вероятности, Р(А) равна отношению площади кольца к площади большого круга:

Ответ: 0,75

35. В ящике содержится 12 деталей, изготовленных на заводе № 1, 20 деталей - на заводе № 2 и 18 деталей - на заводе № 3. Вероятность того, что деталь, изготовленная на заводе № 1, отличного качества, равна 0,9; для деталей, изготовленных на заводах № 2 и № 3, эти вероятности соответственно равны 0,6 и 0,9. Найти вероятность того, что извлеченная наудачу деталь окажется отличного качества.

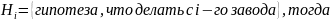
По формуле полной вероятности:

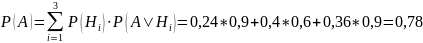
Ответ: 0,78

36. Для случайной величины 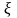, заданной плотностью распределения вероятности найдите значение параметра с, , , ,

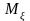если a= 4, b=5, d=0.7.

Ответ: ; ; ;

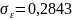
37. Случайный вектор равномерно распределен в треугольнике ABC. Найдите плотность распределения вектора и ковариацию его координат.

A	B	C
(1;3)	(2;3)	(1;5)

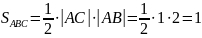
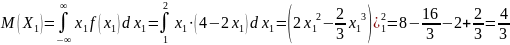
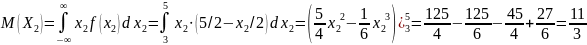
Ответ: ;

38. Для случайной величины , заданной плотностью распределения вероятности найдите значение параметра с, , , если a= 4, b=5, d=0.7.

Ответ: ; ; ;

39. 4. Случайный вектор равномерно распределен в треугольнике ABC. Найдите условную плотность распределения .

A	B	C
(1;3)	(2;3)	(1;5)

Ответ:

40. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго 0,8. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.

p₁ = 0,7 - вероятность попадания первого стрелка при одном выстреле

p₂ = 0,8 - вероятность попадания второго стрелка при одном выстреле

А={при одном залпе в мишень попал только один из стрелков}

Ответ: 0,38

8. Численные методы

41. Построить интерполяционный многочлен Лагранжа по таблице функции:

Запишем формулу для интерполяционного многочлена в форме Лагранжа:

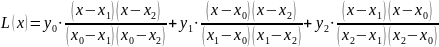
Подставим в формулу табличные значения:

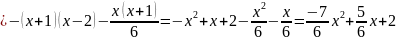
Ответ: интерполяционный многочлен Лагранжа имеет вид

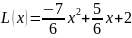
42. Локализовать корни уравнения 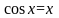и привести фрагмент программного кода на одном из универсальных языков программирования (C++, Pascal, Java и т. п.) для нахождения этих корней методом бисекций с точностью .

корень между нулем и единицей

43. Построить интерполяционный кубический сплайн 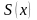по таблице функции: ,

при граничных условиях , .

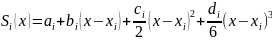
с₀=0 , с₂=1

Обозначим:

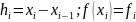
Формулы для вычисления коэффициентов сплайна:

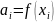
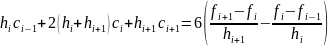
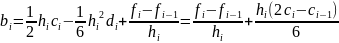
Найдем коэффициенты сплайна:

Тогда

при х₁=0

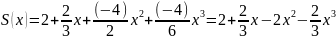
Ответ:

44. Напишите фрагмент программного кода на одном из универсальных языков программирования (C++, Pascal, Java и т. п.) для приближенного вычисления интеграла методом парабол с разбивкой области интегрирования на 100 частичных отрезков.

45. Напишите фрагмент программного кода на одном из универсальных языков программирования (C++, Pascal, Java и т. п.) для численного решения задачи Коши методом Рунге-Кутта 4-го порядка на отрезке с шагом .

const

n=20;

var

k1,k2,k3,k4,x,y: array [0..n] of real;

h: real;

i: integer;

function f(x,y: real): real;

begin

f:=(x*sin(y));

end;

begin

h:=0.1;

y[0]:=1;

for i:=0 to n do

x[i] :=i*h;

for i:=0 to n-1 do

begin

k1[i]:=f(x[i],y[i]);

k2[i]:=f(x[i]+h/2,y[i]+h*k1[i]/2);

k3[i]:=f(x[i]+h/2,y[i]+h*k2[i]/2);

k4[i]:=f(x[i]+h,y[i]+h*k3[i]);

y[i+1]:=y[i]+h/6*(k1[i]+2*k2[i]+2*k3[i]+k4[i]);

end;

for i := 0 to n do

writeln('x[',i:2,'] = ',x[i]:0:1,' y[',i,'] = ',y[i]:0:4);

readln;

end.

Получили

x[ 0] = 0.0 y[0] = 1.0000

x[ 1] = 0.1 y[1] = 1.0042

x[ 2] = 0.2 y[2] = 1.0169

x[ 3] = 0.3 y[3] = 1.0383

x[ 4] = 0.4 y[4] = 1.0687

x[ 5] = 0.5 y[5] = 1.1086

x[ 6] = 0.6 y[6] = 1.1584

x[ 7] = 0.7 y[7] = 1.2187

x[ 8] = 0.8 y[8] = 1.2900

x[ 9] = 0.9 y[9] = 1.3725

x[10] = 1.0 y[10] = 1.4664

x[11] = 1.1 y[11] = 1.5712

x[12] = 1.2 y[12] = 1.6860

x[13] = 1.3 y[13] = 1.8089

x[14] = 1.4 y[14] = 1.9377

x[15] = 1.5 y[15] = 2.0692

x[16] = 1.6 y[16] = 2.2000

x[17] = 1.7 y[17] = 2.3268

x[18] = 1.8 y[18] = 2.4465

x[19] = 1.9 y[19] = 2.5567

x[20] = 2.0 y[20] = 2.6559