Оглавление
Математический анализ 1
Комплексный анализ 4
3. Функциональный анализ 5
Дискретная математика 7
Дифференциальные уравнения 9
Теория вероятностей и математическая статистика 12
8. Численные методы 15
Методы оптимизации. Теория игр и исследование операций 19
Математический анализ
1.
Найти предел
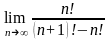 .
.

2. Найти предел .

3.
Исследовать функцию на непрерывность
 .
.

Знаменатель функции обращается в ноль при х=3. Исследуем ф-ю на непрерывность в этой точке:

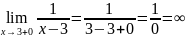
В точке х=3 функция терпит неустранимый разрыв второго рода
4.
Найти производную функции
 .
.

5. Найти частные производные второго порядка по всем переменным функции
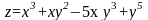 .
.


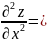

6.
Исследовать функцию на экстремум, найти
точки перегиба и интервалы выпуклости
и вогнутости её графика
 .
.

Найдем точки подозрительные на экстремум:




y(х)
возрастает при х
 (-∞;1/3)
(-∞;1/3) (3;∞)
, убывает при х
(1/3; 3)
(3;∞)
, убывает при х
(1/3; 3)


Найдем точки перегиба:

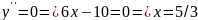
y (x)
вогнута при х
(5/3 ;
(x)
вогнута при х
(5/3 ; )
, выпукла при х
(-∞; 5/3)
)
, выпукла при х
(-∞; 5/3)
х=5/3 точка перегиба
7.
Найти интеграл
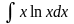 .
.

8.
Вычислить площадь фигуры, ограниченной
линиями
 и
и
 .
.

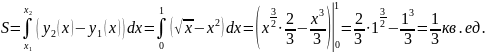
Ответ:

9 .
Вычислить интеграл
.
Вычислить интеграл
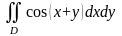 ,
где D - область, ограниченная
прямыми
,
где D - область, ограниченная
прямыми
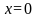 ,
,
 ,
,
 .
.

Ответ:
10.
Вычислить криволинейный интеграл
 ,
где L - дуга параболы
от точки (0;0) до точки (1;1).
,
где L - дуга параболы
от точки (0;0) до точки (1;1).
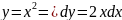
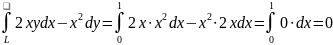
11.
Исследовать ряд на сходимость
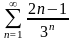 .
.
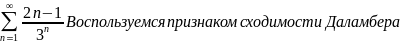

следовательно
ряд
 сходится
сходится
Ответ: сходится
12.
Найти область сходимости ряда
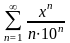 .
.

Воспользуемся признаком сходимости Даламбера:

Требуем,
чтобы
 , следовательно
, следовательно

Исследуем сходимость на границах интервала:


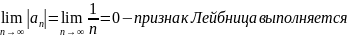
Ответ:

13. Исследовать ряд на абсолютную и
условную сходимость
 .
.

Проверим выполнение признака Лейбница:

Следовательно ряд сходится условно, исследуем абсолютную сходимость:
 ряд расходится как обобщенный
гармонический с k=1/2 <1
ряд расходится как обобщенный
гармонический с k=1/2 <1
следовательно абсолютная сходимость не выполняется
Ответ: сходится условно
Комплексный анализ
14.
Вычислить
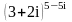 ,
явно выделив действительную и мнимую
части.
,
явно выделив действительную и мнимую
части.



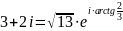
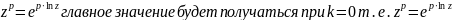



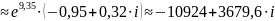
15.
Разложить в ряд Лорана функцию

Точка z=0 является особой точкой функции, других особых точек функция не имеет. Ряд Лорана для данной функции будет только один и сходиться он будет в области |z|>0.
В
известном разложении
 заменяем z на –1/z2
и получаем
заменяем z на –1/z2
и получаем

3. Функциональный анализ
16.
Дано пространство
 и в нем скалярное произведение
и в нем скалярное произведение .
Проверить, что оно удовлетворяет аксиомам
скалярного произведения.
.
Проверить, что оно удовлетворяет аксиомам
скалярного произведения.
Аксиомы скалярного произведения:
Аксиома 1 определяет симметричность скалярного произведения, аксиомы 2 и 3 — аддитивность и однородность по первому сомножителю, аксиома 4 — неотрицательность скалярного квадрата.
для
Аксиомы 1,2,3
выполняются в силу свойств определенного
интеграла. Проверим выполнение аксиомы
4. Для ненулевой функции
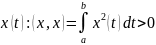 , так как, если в какой-нибудь точке
, так как, если в какой-нибудь точке
 функция
функция
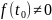 , то в силу непрерывности она отлична
от нуля в некоторой окрестности точки
, то в силу непрерывности она отлична
от нуля в некоторой окрестности точки
 , целиком лежащей в интервале (а,в).
Поэтому интеграл от
, целиком лежащей в интервале (а,в).
Поэтому интеграл от
 в этой окрестности больше нуля.
в этой окрестности больше нуля.
Таким образом пространство и в нем скалярное произведение является евклидовым.
17.
Убедитесь, что функция
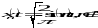 образует ортонормированную систему
функций в пространстве
образует ортонормированную систему
функций в пространстве
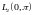 .
.
Скалярное произведение любых двух элементов системы должно равняться нулю и иметь норму равную единице.




18. Является ли заданное отображение линейным оператором в V3 :
А: (х1, х2, х3) -> (х1-х2, х2+3х3-х1, х3+5х2) в базисе из единичных векторов.
Чтобы А являлся линейным оператором должно выполняться:

Найдем А=
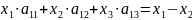
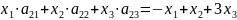

A= линейный оператор приводящий (х1,
х2,
х3)
-> (х1-х2,
х2+3х3-х1,
х3+5х2)
линейный оператор приводящий (х1,
х2,
х3)
-> (х1-х2,
х2+3х3-х1,
х3+5х2)
19. Является ли
группой множество квадратных матриц
второго порядка вида
 ,
определители которых равны 1, где (a,
b,
c,
d)
\in R
относительно операции умножения матриц.
,
определители которых равны 1, где (a,
b,
c,
d)
\in R
относительно операции умножения матриц.
Так как для операции умножения квадратных матриц второго порядка выполняется свойство ассоциативности мы можем считать множество квадратных матриц второго порядка вида , определители которых равны 1, где (a, b, c, d) \in R относительно операции умножения матриц полугруппой.
Полугруппа называется группой, если в ней существует нейтральный элемент и для любого ее элемента существует обратный относительно операции умножения.
Нейтральный элемент – это элемент, для которого выполняется свойство коммутативности при операции умножения: A*e = e*A.
Во множестве квадратных матриц второго порядка вида , определители которых равны 1, где (a, b, c, d) \in R есть такой элемент - это единичная матрица второго порядка.
Так как определитель любого элемента данного множества равен 1, любой элемент из этого множества имеет обратный относительно операции умножения.
Вывод: множество квадратных матриц второго порядка вида , определители которых равны 1, где (a, b, c, d) \in R относительно операции умножения матриц является группой.
20. Записать параметрическое уравнение гиперплоскости (A1 A2 A3 A4 A5).
A1 |
A2 |
A3 |
A4 |
A5 |
||||||||||||||||||||||||
-3 |
-8 |
-3 |
3 |
1 |
-9 |
-1 |
-9 |
-2 |
1 |
2 |
3 |
-4 |
4 |
5 |
3 |
-9 |
-3 |
-8 |
-3 |
3 |
1 |
-9 |
-1 |
-9 |
||||
Найти базис направляющего подпространства