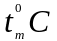- •1)Расчет среднеповерхностной температуры нагретой зоны герметичной рэа.
- •2)Расчёт теплового режима кассетной рэа группы a.
- •3)Расчет теплового режима кассетной рэа группы б.
- •1)Расчет среднеповерхностной температуры нагретой зоны герметичной рэа
- •2)Расчёт теплового режима кассетной рэа группы a.
- •3)Расчет теплового режима кассетной рэа группы б.
2)Расчёт теплового режима кассетной рэа группы a.
Исходные данные для варианта 8:
размеры нагретой зоны Lx=0,2м., Ly=0,4м., Lz=0,15м.;
усредненные размеры элементарной ячейки lx=0,015м., ly=0,02м., lz=0,015м.;
усредненные размеры модуля l2x=0,01м., l2y=0,01м., l2z=0,009м.;
толщина платы δ=0,002м.;
среднеповерхностная температура зоны tз=30°C
суммарная мощность источников тепла P=60Вт;
8.усредненные
коэффициенты теплопроводности модуля
λ2x=0,3
Вт/ град,λ2y=0,2
Вт/
град,λ2z=0,25
Вт/
град,платы
λ1=0,3
Вт/
град,
и газа λ2=0,2
Вт/
град;
град,λ2y=0,2
Вт/
град,λ2z=0,25
Вт/
град,платы
λ1=0,3
Вт/
град,
и газа λ2=0,2
Вт/
град;
1.Определить размер областей элементарной ячейки:
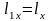 =0,015м.
=0,015м. 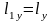 =0,02м.
=0,02м. 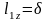 =0,002м.
=0,002м.
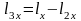 =0,005м.
=0,005м.  =0,01м.
=0,01м. 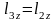 =0,009м.
=0,009м.
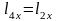 =0,01м.
=0,01м. 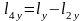 =0,01м.
=0,01м. 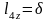 =0,002м.
=0,002м.
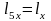 =0,015м.
=0,015м. 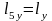 =0,02м.
=0,02м. 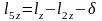 =0,004м.
=0,004м.
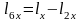 =0,005м.
=0,005м. 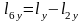 =0,01м.
=0,01м. 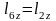 =0,009м.
=0,009м.
2.Вычислить тепловые проводимости областей элементарной ячейки:
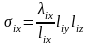 ;
; 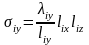
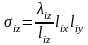
для i = 1, ..., 6 при α1x = α1y = α1z = α1;
α3x = α3y = α3z = α4z = ... = α6x = α2
3.По формулам., приведенным на рис. 3, определить проводимости σx, σy, σz элементарной ячейки.
4.Вычислить коэффициенты теплопроводности анизотропного тела
=0, Вт/ град; =0, Вт/ град; =0,322 Вт/ град
5.Вычислить параметры
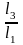 =0,58,
=0,58,
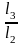 =0,28,
где
=0,28,
где
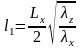 =0,13м.;
=0,13м.;
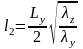 =0,28м.;
=0,28м.;
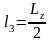 =0,075м.
=0,075м.
и по рис. 4 определить значение С=0,45
6.Определить температуру в центре нагретой зоны
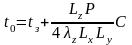 =69,3°C
=69,3°C
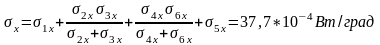
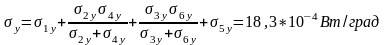
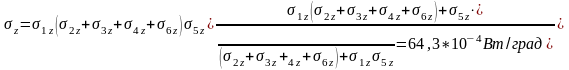
Рис. 3. Тепловые схемы элементарной ячейки
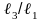
Рис. 4. График для определения параметра С
3)Расчет теплового режима кассетной рэа группы б.
Исходные данные для варианта 8:
- размеры корпуса L1=0,22м., L2=0,2м., H=0,3м.;
- расстояние между посадочными местами кассет b=0,02м;
-
объем кассеты с деталями Vд=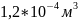
- число кассет n=10;
-
степень черноты корпусов и кассет
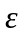 =0,9;
=0,9;
-
температура корпуса tк=20
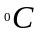
- мощность, выделяющаяся внутри РЭА Р=25 Вт.
Определить геометрические размеры нагретой зоны
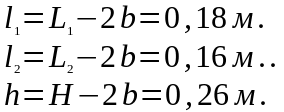
эффективную толщину кассеты
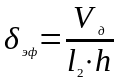 =2,88
=2,88
и эффективное расстояние между кассетами
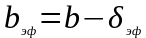 =0,0171м.
=0,0171м.
Задаться начальным значением температуры зоны
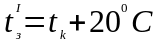 =40
.
=40
.
Определить тепловую проводимость
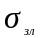 :
:
Площадь излучающей поверхности
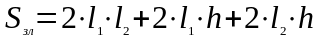 =0,234
=0,234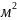 .
.
Коэффициент теплоотдачи
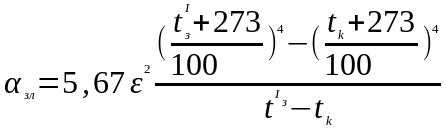 =5,12
Вт/
град
=5,12
Вт/
град
Проводимость
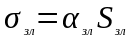 =1,12
Вт/град.
=1,12
Вт/град.
4.
Определить проводимость
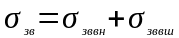 ,
,
где
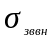 - проводимость “зона-воздух”, внутренних
поверхностей кассет;
- проводимость “зона-воздух”, внутренних
поверхностей кассет;
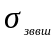 -
проводимость “зона-воздух” внешний
(т.е. обращенных к корпусу) поверхностей
кассет.
-
проводимость “зона-воздух” внешний
(т.е. обращенных к корпусу) поверхностей
кассет.
4.1. Площадь “зона-воздух” внутренних поверхностей кассет
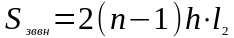 =0,75
=0,75
4.2. Коэффициент теплоотдачи при движении воздуха между двумя нагретыми плоскостями
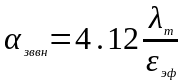 =6,46
Вт/
град
=6,46
Вт/
град
где - теплопроводность воздуха при температуре
=30 .
4.3.
Проводимость
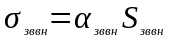 =4,85
Вт/град.
=4,85
Вт/град.
4.4. Площадь “зона-воздух” внешних поверхностей кассет
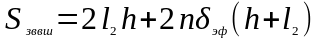 =0,107
=0,107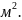
4.5. Коэффициент теплоотдачи при турбулентном движении воздуха
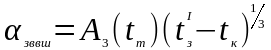 =4,26
Вт/
град
=4,26
Вт/
град
где
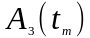 – определяется по табл. 6.
– определяется по табл. 6.
4.6.
Проводимость
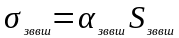 =0,456
Вт/град.
=0,456
Вт/град.
4.7. Суммарная проводимость =5,3 Вт/град.
5.
Вычислить проводимость «воздух-корпус»
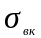
5.1. Площадь внутренней поверхности корпуса
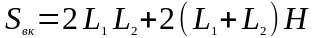 =0,34
=0,34
5.2.
Коэффициент теплоотдачи
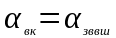 =4,26
Вт/
град
=4,26
Вт/
град ,
так как характер движения воздуха тот
же.
,
так как характер движения воздуха тот
же.
Таблица 5.
Значения для воздуха
|
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
110 |
|
0,026 |
0,0268 |
0,0276 |
0,0283 |
0,029 |
0,0297 |
0,0305 |
0,0313 |
0,0321 |
0,0329 |
Таблица 6.
Значения для воздуха
|
10 |
20 |
30 |
40 |
60 |
80 |
100 |
|
1,65 |
1,61 |
1,57 |
1,53 |
1,45 |
1,39 |
1,33 |
5.3.
Проводимость
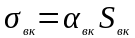 =1,45
Вт/град.
=1,45
Вт/град.
6.
Определить проводимость “зона-корпус”
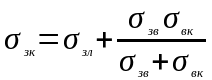 =2,26
Вт/град.
=2,26
Вт/град.
7. Вычислить температуру зоны в следующем приближении
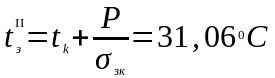
Если , то конец. Иначе установить и перейти к п.3.При повторном расчёте =31,85 . Новая температура отличается от прежней меньше, чем на 5%,что свидетельствует о правильности полученного результата.
Заключение.
В настоящей работе мною были проведены примерные расчёты для температуры среднеповерхностной нагретой зоны герметичной РЭА,температуры в центре нагретой зоны для теплового режима кассетной РЭА групп А и Б.Проведённые мною расчёты соответствуют алгоритмам. Полученные результаты правильны.
Список источников.
Учебное пособие в электронной форме.