
- •Теорема Коши.
- •Правило Лопиталя.
- •Признаки монотонности функции.
- •Э кстремум функции.
- •Необходимое условие экстремума дифференцируемой функции.
- •Замечание 2. Функция имеет экстремум только в критических точках. Достаточное условие экстремума.
- •Наибольшее и наименьшее значения функции на отрезке.
- •Выпуклые и вогнутые функции.
- •Асимптоты графика функции.
- •Первообразная и неопределенный интеграл.
- •Замена переменных в неопределенном интеграле.
- •Интегрирование по частям в неопределенном интеграле.
- •Интегрирование выражений, содержащих квадратный трехчлен.
- •Интегрирование рациональных дробей.
- •Интегрирование некоторых иррациональных алгебраических функций.
- •Интегрирование тригонометрических выражений.
- •1Й случай.
- •2Й случай.
- •Определенный интеграл. Задача о площади криволинейной трапеции.
- •Определение определенного интеграла.
- •Теорема о существовании определенного интеграла.
- •Вычисление площади плоских фигур в декартовой системе координат.
- •Полярная система координат.
- •Изображение линий в полярной системе координат.
- •Связь между декартовой и полярной системами координат.
- •Вычисление площади криволинейного сектора.
- •Объем тела вращения.
- •Функции нескольких переменных.
- •Функции 2 переменных, способы задания, область определения.
- •Частные производные функций 2 переменных и их геометрический смысл.
- •Дифференцирование сложной функции.
- •Производная неявной функции.
- •Геометрический смысл полного дифференциала функции двух переменных.
- •Частные производные высших порядков.
- •Экстремум функции 2 переменных.
- •Наибольшее и наименьшее значение функции в замкнутой области.
- •Производная по направлению и градиент.
Объем тела вращения.
Определение: Если криволинейная трапеция ограничена линиями y=0; x=a; x=b; y=f(x), где f(x)0вращается вокруг оси OX, то полученное тело называется телом вращения вокруг оси OX.
Как
известно, объем тела выражается через
площадь поперечного сечения по формуле:
.
В данном случае поперечными сечениями
являются круги радиусом Rкр=f(x);
Sкр=S(x)
= f2(x)
VOX=
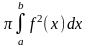 .
.
Если
фигура, ограниченная кривыми y1=f1(x)
и y2=f2(x)
[0 ]
и прямыми x=a,
x=b,
вращается вокруг оси Ох, то объем тела
вращения
]
и прямыми x=a,
x=b,
вращается вокруг оси Ох, то объем тела
вращения
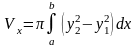

Если
криволинейная трапеция ограниченная
линиями
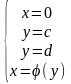 вращается
вокруг оси OY,
то объем полученного тела вращения
VOY=
вращается
вокруг оси OY,
то объем полученного тела вращения
VOY=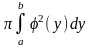 .
.
Пример: Вычислить объем тела вращения, ограниченного линиями y=0; x=0; x=1; y=ex.

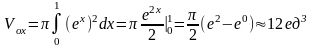
Функции нескольких переменных.
Определение:
Пусть задано множество упорядоченных
наборов чисел
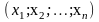 ,
принадлежащее некоторой n-мерной
области D.
Правило (закон), который ставит в
соответствие каждому набору чисел
,
принадлежащее некоторой n-мерной
области D.
Правило (закон), который ставит в
соответствие каждому набору чисел
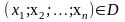 единственное значение
единственное значение
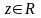 называется функцией
нескольких переменных
называется функцией
нескольких переменных
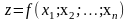 ,
действующей из D
в R
(DR).
При этом
,
действующей из D
в R
(DR).
При этом
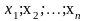 называются независимыми переменными,
а z
– зависимой переменной.
называются независимыми переменными,
а z
– зависимой переменной.
Функции 2 переменных, способы задания, область определения.
Определение:
Пусть задано множество упорядоченных
пар чисел (x;y),
принадлежащее плоской области D.
Правило (закон), который ставит в
соответствие каждой паре чисел
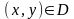 единственное значение
называется функцией
двух переменных
единственное значение
называется функцией
двух переменных
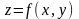 ,
действующей из D
в R
(DR).
При этом x
и y
называются независимыми переменными,
а z
– зависимой переменной.
,
действующей из D
в R
(DR).
При этом x
и y
называются независимыми переменными,
а z
– зависимой переменной.
Множество
 называется областью
определения функции;
множество значений, принимаемых z
в области определения называется
областью
значений функции,
обозначается E
или
называется областью
определения функции;
множество значений, принимаемых z
в области определения называется
областью
значений функции,
обозначается E
или
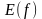 .
.
Определение: Графиком функции называется множество точек пространства с координатами (x,y,f(x,y)),таких, что (x,y)D(z)-область определения функции. Для функции двух переменных графиком является некоторая поверхность.
Частные производные функций 2 переменных и их геометрический смысл.
Пусть
функция
определена в окрестности точки M(x,y)
и в самой точке М. Дадим переменной x
приращение x
(xx+x),
а переменную y
оставим без изменения (yy)так,
чтобы точка M1(x+x;
y)указанной
окрестности, тогда функция получит
приращение xz
по переменной x:
 .
.
Определение:
Если существует предел при x0
отношения приращения функции к приращению
аргумента, то он называется частной
производной функции z
по переменной x
и обозначается
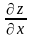 :
:
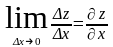 .
.
Определение:
Если существует предел при
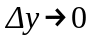 отношения приращения функции к приращению
аргумента, то он называется частной
производной функции z
по переменной y
и обозначается
отношения приращения функции к приращению
аргумента, то он называется частной
производной функции z
по переменной y
и обозначается
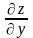 :
:
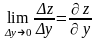 .
.
При вычислении частных производных все переменные, кроме одной (по которой берется производная) считаются константами. Берем функцию двух переменных, частное по x, y – константа.
 ,
y-const.,
x-const
или
,
y-const.,
x-const
или
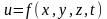
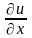 y,z,t-const.,
y,z,t-const.,
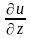 x,y,t-const..
x,y,t-const..
Пример:
Вычислить частные производные функции двух переменных.
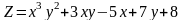 ;
;
Решение:
 (y-const);
(y-const);
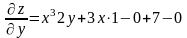 (x-const).
(x-const).
Дифференцирование сложной функции.
Пусть
функция z=f(x,y)
– функция двух переменных, x
и y,
каждая из которых является функцией
независимой переменной t,
 В этом случае
функция z=f(x(t),y(t))
является сложной функцией одной
независимой переменной t;
переменные x
и y
– промежуточные переменные.
В этом случае
функция z=f(x(t),y(t))
является сложной функцией одной
независимой переменной t;
переменные x
и y
– промежуточные переменные.
Теорема:
Если
z=f(x,y)
– дифференцируемая в точке
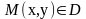 функция
и
функция
и
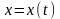 и
и
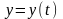 — дифференцируемые функции независимой
переменной t,
то производная сложной функции
z=f(x(t),y(t))
вычисляется по формуле:
— дифференцируемые функции независимой
переменной t,
то производная сложной функции
z=f(x(t),y(t))
вычисляется по формуле: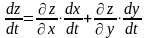
Общий случай: z=f(x,y), где x=x(u,v), y=y(u,v) то есть z=f(x(u,v),y(u,v)) – сложная функция независимых переменных u и v, частные производные которой находятся по формулам:

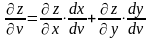
Таким образом, производная сложной функции z по каждой независимой переменной (u и v) равна сумме произведений частных производных этой функции по ее промежуточным переменным на их производные по соответствующей независимой переменной.
Пример:
Найти
 и
и
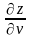 ,
если
,
если
 и
и
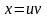 ,
,
 .
.
Решение:
Найдем .
 .
.
Упростим правую часть выражения:
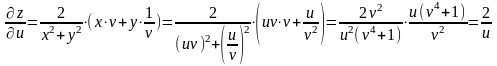 ,
то есть
,
то есть
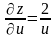
Найдем .
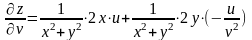
Упростим правую часть выражения:
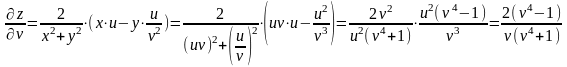 ,
то есть
,
то есть
 .
.
