Изображение линий в полярной системе координат.

= R – окружность с центром в полюсе и радиусом R.

=  - луч под углом к полярной оси.

=  – при построении любой кривой в полярной системе координат, нужно задавать различные значения полярного угла  и вычислять соответственно значения полярного радиуса . Если  получится меньше нуля, то картинки не будет (этой части рисунка не будет)

Спираль Архимеда	Кардиоида	3-х лепестковая роза		Лемниската Бернулли
=	=1+cos	=cos3	=4cos	2=cos2

Связь между декартовой и полярной системами координат.

Если полярную и декартову систему координат совместить так, чтобы полюс совпал с началом координат, а полярная ось с положительным направлением оси 0x, то можно получить формулы перехода от полярных координат (; ) к декартовым (x;y):

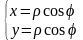, и от декартовых к полярным: ,

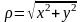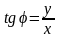
Вычисление площади криволинейного сектора.

Если в декартовой системе координат вычисляется площадь криволинейной трапеции, то в полярной системе вычисляется площадь криволинейного сектора.

Определение: Криволинейным сектором называется фигура, заключенная между двумя лучами, выходящими из полюса под углами  и  и кривой, заданной в полярной системе координат =().

Разобьем криволинейный сектор лучами =_i, i = 0…n на части

=₀<₁<₂<…<_n=

 =,  =,  =().

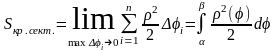
В ПСК: S= .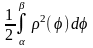

Вычисление длины дуги кривой в декартовой системе координат.

.

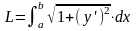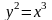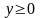Пример: Вычислить длину полукубической параболы , где , x=0, x=1.

; .

.

= = = = = = =

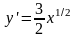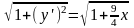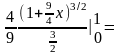
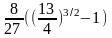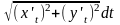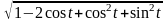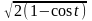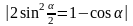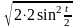L=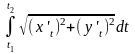 = =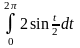 = =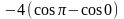-4(-1-1)=8.

Вычисление длины дуги кривой L, заданной в полярной системе координат.

Пусть кривая L задана в полярной системе координат:

.

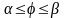Длина дуги кривой в полярной системе координат L= .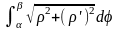

Пример: Вычислить длину кардиоиды .

В силу симметричности кривой вычислим ½ длины.

_{½L= .}

= =

= = = = =

= =

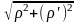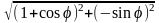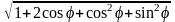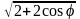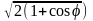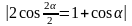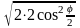½L= = =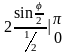4(1-0)=4 L=4∙2=8.

Вычисление объема тела по площадям параллельных сечений.

Пусть дано некоторое тело и известно, что площадь поперечного сечения плоскости перпендикулярна оси OX. Разобьем тело на части плоскостями x=x_i перпендикулярными оси OX. Отрезок [a,b], лежащий на оси OX, разобьется соответственно точками x_i на n частей: a=x₀<x₁<x₂<…<x_n=b. x_i = x_i+1 – x_i- длина [x_i ; x_i+1]. В каждой точке x принадлежащей отрезку [a,b] известно поперечное сечение этого тела, то есть площадь поперечного сечения является функцией от x(S(x)). На i-ом отрезке выберем произвольную точку с_i и заменим объем i части тела объемом прямого цилиндра V_i = S_осн высоту=S(с_i) x_i ; объем тела приближенно равен сумме объемов прямых цилиндров V_T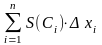 . Причем равенство будет, вообще говоря, тем точнее, чем мельче будет разбиение. Переходя к пределу, получаем V_T=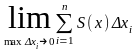 . 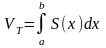Этот предел интегральных сумм является определенным интегралом , где S(x) – площадь поперечного сечения.