Интегрирование некоторых иррациональных алгебраических функций.

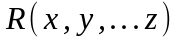
Пусть  рациональная функция своих аргументов. Тогда интеграл 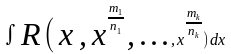находится заменой переменных

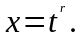
Как правило, за 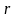берется наименьшее общее кратное чисел 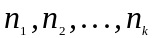, где 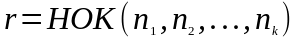, т.е. r выбирается так, чтобы все корни, стоящие под знаком интеграла, извлекались.

Пример 1. Вычислить неопределенный интеграл .

Решение:

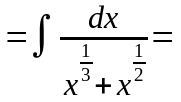
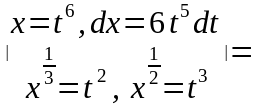
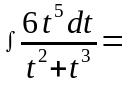
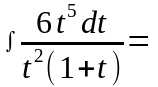
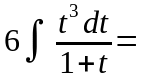
В подынтегральном выражении выделим целую часть: ,

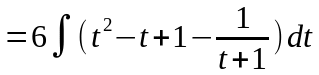
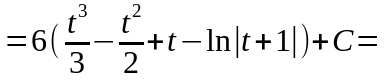
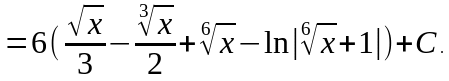
Интегрирование тригонометрических выражений.

Пусть — рациональная функция своих аргументов. Рассмотрим несколько случаев:

1Й случай.

Интеграл 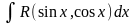универсальной тригонометрической подстановкой 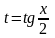сводится к интегралу от рациональной функции. При этом .

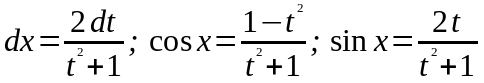С учетом сделанной замены получим

,

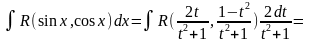
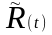
где  рациональная функция, интеграл от которой рассматривался выше.

Пример: Найти неопределенный интеграл: .

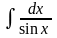Решение: Сделаем универсальную тригонометрическую подстановку:

; .

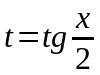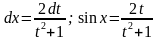Тогда .

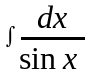
Отметим, что универсальную тригонометрическую подстановку, как правило, используют в тех случаях, когда другие подстановки, приведенные ниже не приводят к желаемым результатам.

2Й случай.

В интегралах 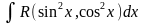, где и 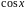входят в подынтегральную рациональную функцию, только в четных степенях делается замена 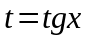. При этом

.

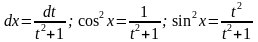Этой же подстановкой к интегралам от рациональных функций приводятся интегралы вида .

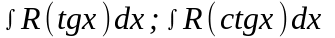Пример: Найти неопределенный интеграл:

.

Решение: Сделаем подстановку:

; .

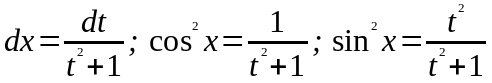Тогда

.

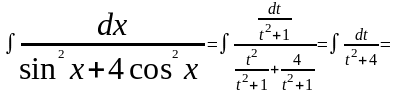
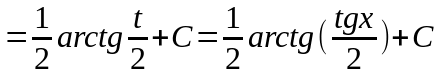3-й случай. Интегрирование выражений вида

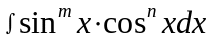, (6)

где m и nцелые числа. Рассмотрим два случая:

а) Среди чисел m,n есть хотя бы одно нечетное. Тогда за t принимается функция, стоящая в основании другой степени.

Пример. Найти неопределенный интеграл:

.

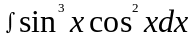Решение: Здесь функция стоит в нечетной степени, поэтому

;

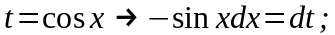
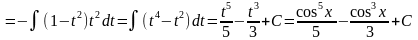б) В выражении (6) оба числа m,n  четные неотрицательные.

Положим m=2p, n=2q и применим формулы:

.

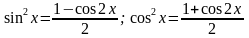Тогда

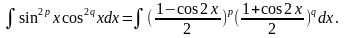
Раскрыв скобки, получим сумму интегралов, к каждому из которых применим 1-й или 2-й способы:

.

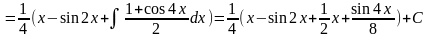Определенный интеграл. Задача о площади криволинейной трапеции.

Определение: Криволинейной трапецией называется фигура, ограниченная линиями x=a; x=b; y=0; y=f(x)0

Р азобьем основание криволинейной трапеции отрезок [a,b] на n частей точками a=x₀<x₁<x₂<…<x_n=b. Обозначим через x_i=x_i – x_i-1 длину i-го отрезка.

В каждом отрезке выберем произвольную точку

C_i[ x_i, x_i-1] и вычислим в ней значение функции f(с_i).

Заменим площадь i-й части криволинейной трапеции площадью прямоугольника с основанием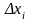 и высотой f(с_i): ;

.

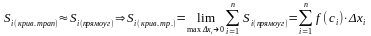Причем равенство, вообще говоря, будет тем точнее, чем меньше разбиение.

Определение определенного интеграла.

Пусть функция y=f(x) определена на отрезке [a,b]. Разобьем отрезок [a,b] на части точками a=x₀<x₁<x₂<…<x_n=b. Обозначим через x_i=x_i – x_i-1 .

В каждом из отрезков возьмем точку с_i[ x_{i -1}, x_i] и вычислим в ней значение функции f(с_i). Составим сумму S_n= , которую в дальнейшем будем называть интегральной суммой. Если существует предел интегральных сумм при max│x_i│0, который не зависит ни от способов разбиения отрезка [a,b] на части, ни от способов выбора точек с_i, то он называется определенным интегралом от функции f(x) по промежутку . .

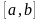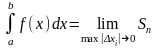Здесь a – нижний предел, b – верхний предел, f(x) – подынтегральная функция, f(x)dx– подынтегральное выражение.