Замена переменных в неопределенном интеграле.
Пусть
функция является дифференцируемой и
обратимой
,
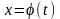на множестве значений которой определена
функция
=
.
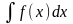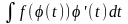Пример:
=
=
=
=
=
=
.
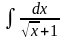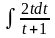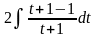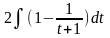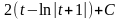Интегрирование по частям в неопределенном интеграле.
Т.к.
.
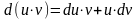
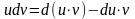Проинтегрируем обе части равенства:
.
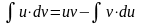Интегрирование по частям применяют, когда сложный интеграл можно заменить интегрированием более простого. Рассмотрим применение метода в следующих случаях:
1. Подынтегральная функция представляет собой произведение многочлена на показательную функцию или тригонометрическую. За u берется многочлен, за dv – оставшуюся часть подынтегрального выражения.
Пример:
=
=
=
=
.
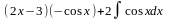2. Подынтегральная функция представляет собой произведение многочлена на логарифмическую или обратную тригонометрическую функцию. За часть u нужно взять логарифмическую или обратную тригонометрическую функцию.
Пример:
=
=
=
=
=
.
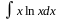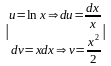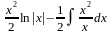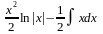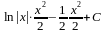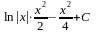3. Подынтегральная функция представляет собой произведение тригонометрической на показательную функцию. Не важно что брать за u.
Пример:
I=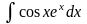
=
=
=
=
.
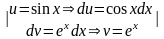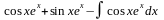Последний интеграл есть не что иное как исходный интеграл, поэтому можно
записать:
;
;
.
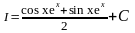Интегрирование выражений, содержащих квадратный трехчлен.
;
.
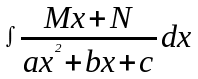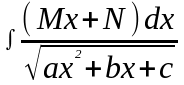Каждый из указанных двух интегралов берется в два приема:
а) выделяется полный квадрат в квадратном трехчлене:
;
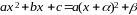б)
заменой
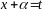исходный интеграл сводится к табличным
интегралам.
Пример: Найти неопределенный интеграл.
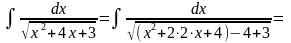
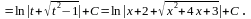
Интегрирование рациональных дробей.
Выражения
вида
,
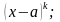
где а
вещественное, k,
l
натуральные числа, а квадратный трехчлен
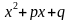не имеет действительных корней, назовем
простейшими сомножителями.
Известна
основная теорема алгебры:
любой многочлен
степени n
можно разложить в произведение простейших
сомножителей:
=
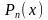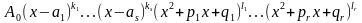(4)
где
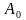число;
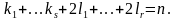
Дроби
вида
,
где k,
l
натуральные
числа,
простейший сомножитель, будем называть простейшими рациональными дробями.
Определение.
Дробь
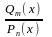называется правильной,
если
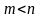(здесь
m и n степени многочленов, стоящих в числителе и в знаменателе, соответственно. Если m≥n , дробь называется неправильной.
Каждую
неправильную дробь можно представить
в виде суммы многочлена и правильной
дроби: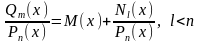
.
Можно доказать следующую теорему.
Теорема.
Любая
правильная рациональная дробь
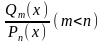, где
многочлен, определённый равенством
(4), может быть представлена в виде суммы
простейших рациональных дробей (m и n —
степени многочленов, стоящих в числителе
и знаменателе соответственно). Эта сумма
строится следующим образом в два этапа:
1)
каждый простейший множитель вида
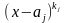порождает следующую сумму из
слагаемых:
;
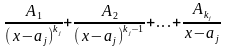2)
каждый сомножитель вида
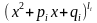порождает следующую сумму из
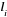слагаемых:
В
результате мы получим следующее
разложение правильной дроби на простейшие:
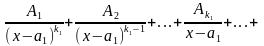
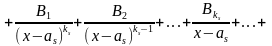
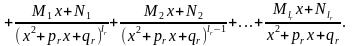(5)
Пример:
Найти
.
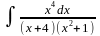Решение: Поскольку рациональная дробь, стоящая под знаком интеграла, является неправильной, то представим ее в виде суммы многочлена и правильной дроби (для этого достаточно найти частное и остаток от деления числителя на знаменатель).
Тогда
.
Разложим
дробь
на простейшие дроби:
;
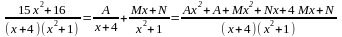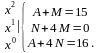
Отсюда
Следовательно,
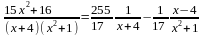
Но тогда:
=
