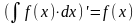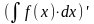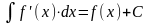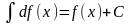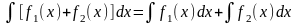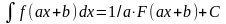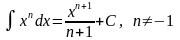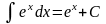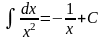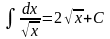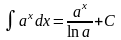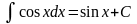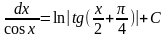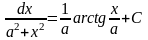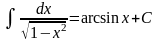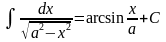Асимптоты графика функции.

Определение: Прямая l называется асимптотой графика функции , если расстояние от точки М на графике до прямой l стремится к нулю при удалении точки М по графику функции от начала координат.

Асимптоты бывают вертикальные, горизонтальные, наклонные.

Вертикальной асимптотой называется прямая x=a, если .

Находят вертикальную асимптоту по точкам разрыва второго рода (бесконечный разрыв).

Наклонной асимптотой называется асимптота, уравнение которой имеет вид: .

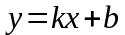Оказывается, что если является асимптотой, то и 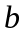в уравнении определяются следующим образом , .

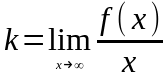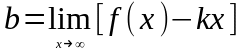Замечание 1: Чтобы у кривой были наклонные асимптоты, нужно, чтобы соответствующие пределы в определении k и b были конечными, причем предел при x→+∞ и предел при x→-∞ нужно вычислять отдельно.

Замечание 2: Если k=0, то y=b. Наклонная асимптота в этом случае называется горизонтальной.

Замечание 3: Кривая никогда не пересекает вертикальную асимптоту, а горизонтальные и наклонные асимптоты кривая может пересекать и даже бесконечное число раз.

Пример: Найти асимптоты графика функции .

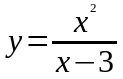D(y): x3.

 x=3 – точка разрыва.

— вертикальная асимптота.

= ;

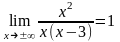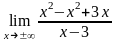= = = =3  .

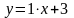Þ 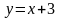— наклонная асимптота.

Схема полного исследования функции.

1. Определить естественную область D(y) определения функции.

2. Исследовать на четность и нечетность.

3. Найти точки пересечения графика функции с осями координат.

4. Найти асимптоты.

5. Найти интервалы возрастания и убывания функции, точки экстремума.

6. Найти интервалы выпуклости графика, точки перегиба.

7. Построить график функции.

Первообразная и неопределенный интеграл.

Определение: Первообразной F(x) для функции f(x) на промежутке называют функцию, производная которой .

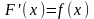Пример. Для функции 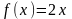: первообразная 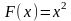на R, так к при любом х.

Лемма.Если производная функции на промежутке 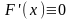, то .

Теорема: Пусть функция F(x) – первообразная f(x), Ф(x) – другая первообразная f(x)  F(x)=Ф(x)+С.

Таким образом, из теоремы следует, что выражение 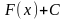описывает все множество первообразных функции f(x).

Определение: Неопределенным интегралом функции f(x) по переменной x называется множество всех её первообразных , где .

 ‒ знак интеграла, f(x) – подынтегральная функция, x – переменная интеграла, 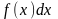‒ подынтегральное выражение, С – const интегрированная.

Вычисление неопределенного интеграла называют интегрированием. Проверить правильность вычисления неопределенного интеграла можно продифференцировав результат.

; - верно.

Свойства неопределенного интеграла.

1
2
3
4
5
6
7

Таблица интегралов.

1		2
3		4
5		6
7		8
9		10
11		12
13		14
15		16
17		18
19		20
21		22
23		24
25		26