
- •Теорема Коши.
- •Правило Лопиталя.
- •Признаки монотонности функции.
- •Э кстремум функции.
- •Необходимое условие экстремума дифференцируемой функции.
- •Замечание 2. Функция имеет экстремум только в критических точках. Достаточное условие экстремума.
- •Наибольшее и наименьшее значения функции на отрезке.
- •Выпуклые и вогнутые функции.
- •Асимптоты графика функции.
- •Первообразная и неопределенный интеграл.
- •Замена переменных в неопределенном интеграле.
- •Интегрирование по частям в неопределенном интеграле.
- •Интегрирование выражений, содержащих квадратный трехчлен.
- •Интегрирование рациональных дробей.
- •Интегрирование некоторых иррациональных алгебраических функций.
- •Интегрирование тригонометрических выражений.
- •1Й случай.
- •2Й случай.
- •Определенный интеграл. Задача о площади криволинейной трапеции.
- •Определение определенного интеграла.
- •Теорема о существовании определенного интеграла.
- •Вычисление площади плоских фигур в декартовой системе координат.
- •Полярная система координат.
- •Изображение линий в полярной системе координат.
- •Связь между декартовой и полярной системами координат.
- •Вычисление площади криволинейного сектора.
- •Объем тела вращения.
- •Функции нескольких переменных.
- •Функции 2 переменных, способы задания, область определения.
- •Частные производные функций 2 переменных и их геометрический смысл.
- •Дифференцирование сложной функции.
- •Производная неявной функции.
- •Геометрический смысл полного дифференциала функции двух переменных.
- •Частные производные высших порядков.
- •Экстремум функции 2 переменных.
- •Наибольшее и наименьшее значение функции в замкнутой области.
- •Производная по направлению и градиент.
Теоремы о дифференцируемых функциях.
Теорема Ферма.
П усть
функция
усть
функция
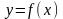 определена и дифференцируема
определена и дифференцируема
на
интервале (a;b) и в некоторой точке x0
этого
интервала принимает наибольшее или
наименьшее значение. Тогда
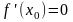 .
.
Геометрический смысл теоремы Ферма:
Так
как
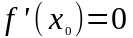 ,
то угловой коэффициент касательной
равен нулю
,
то угловой коэффициент касательной
равен нулю
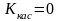
касательная параллельна оси ОХ.
касательная параллельна оси ОХ.
Теорема Ролля.
Пусть
функция
определена и непрерывна на отрезке
[a;b] и дифференцируема на интервале
(a;b), причем на концах интервала принимает
одинаковые значения
 .
Тогда существует точка с(a;b),
значения производной в которой равно
0, т.е.
.
Тогда существует точка с(a;b),
значения производной в которой равно
0, т.е.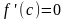 .
.
Геометрический смысл теоремы Ролля:
Þ Ккас=0 Þ касательная
в точке c параллельна оси ОX.
Теорема Лагранжа.
Пусть
функция
определена и непрерывна на отрезке
[a;b] и дифференцируема на интервале
(a;b). Тогда существует точка c(a;b),
значение производной в которой равно
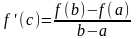 .
.
Геометрический смысл теоремы Лагранжа:
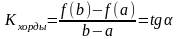
 .
.
Существует точка cÎ(a;b), в которой угловой коэффициент касательной равен угловому коэффициенту хорды, соединяющей граничные точки:
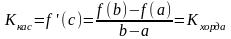 .
.
Найдется такая точка на графике, касательная в которой параллельна хорде, стягивающей концы отрезка [a;b].
Теорема Коши.
Пусть
функции f(x) и g(x) определены и непрерывны
на отрезке [a;b] и дифференцируемы на
интервале (a;b), причем производная функции
g(x) отлична от нуля, g(x)0.
Тогда существует такая точка c(a;b),
для которой выполняется равенство:
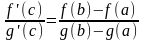 .
.
Правило Лопиталя.
Теорема.
Пусть
функции f(x) и g(x) определены и дифференцируемы
в некоторой окрестности точки x0,
за исключением может быть самой точки
x0,
и
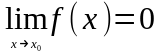 ,
,
 .
Тогда если существует предел отношения
производных функций
.
Тогда если существует предел отношения
производных функций
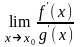 ,
то существует предел отношения самих
функций
,
то существует предел отношения самих
функций
 ,
причем они равны между собой, т.е.
,
причем они равны между собой, т.е.
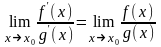 .
.
В дальнейшем это утверждение будем также называть правилом Лопиталя
Замечание.
На практике при раскрытии неопределенности
типа
 можно пользоваться правилом Лопиталя
и в случаях, когда x,
x.
можно пользоваться правилом Лопиталя
и в случаях, когда x,
x.
Для
раскрытия неопределенностей типа
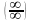 существует аналог правила Лопиталя.
существует аналог правила Лопиталя.
Замечание 1. Правилом Лопиталя можно пользоваться при раскрытии неопределенностей вида (-), (0), (1), (¥0), (00), сводя их к неопределенностям типа , .
Замечание 2. Если после применения правила Лопиталя опять получаем неопределенность вида или , то его можно применить повторно.
Пример: Вычислить пределы по правилу Лопиталя.
1. Чтобы применять правило Лопиталя при неопределенности вида или , нужно продифференцировать отдельно числитель и знаменатель дроби, и вычислить полученный предел.
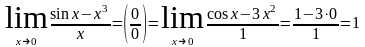 .
.
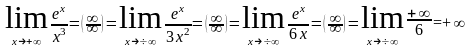 .
.
Вывод: показательная функция (y=an) всегда растет быстрее, чем степенная (у=xn).
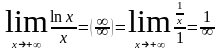 .
.
Вывод: логарифмическая функция (y=logax) растет медленнее, чем степенная.
2. Неопределенность вида (0) нужно преобразовать в неопределенность вида или , опустив один из множителей в знаменатель в отрицательной степени, и потом применять правило Лопиталя.
3. При показательной неопределенности: (00), (1), (0); прежде чем применять правило Лопиталя, нужно прологарифмировать этот предел по основанию e.
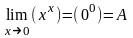 .
.
 =
= =
= =(0×¥)=
=(0×¥)=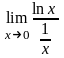 =
=
=
=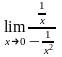 =
=
=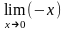 =0;
=0;
 A=e0=1.
A=e0=1.
Формулы Тейлора и Маклорена.
Теорема.
Пусть функция
 n раз дифференцируема в окрестности
точки x0.
Тогда в этой окрестности для функции
справедлива следующая формула Тейлора:
n раз дифференцируема в окрестности
точки x0.
Тогда в этой окрестности для функции
справедлива следующая формула Тейлора:
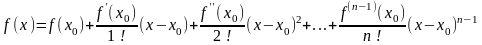 +
+
+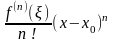 .
.
Здесь
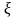 некоторая точка, заключенная между
некоторая точка, заключенная между
 и
и
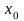 (
(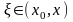 ),
зависящая от
,
а
=
),
зависящая от
,
а
=
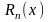 -
остаточный член в форме Лагранжа.
-
остаточный член в форме Лагранжа.
Если x0=0, то формула Тейлора превращается в формулу Маклорена:
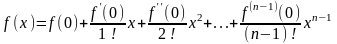 +
+
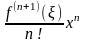
Признаки монотонности функции.
Пусть
функция
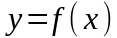 определена и непрерывна на промежутке
(a;b).
определена и непрерывна на промежутке
(a;b).
Определение:
Функция
называется неубывающей
(невозрастающей)
на (a;b), если для любых x1<x2,
принадлежащих (a;b), выполняется
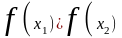 (
).
(
).
Определение:
Функция
называется возрастающей
(убывающей)
на (a;b), если для любых x1<x2,
принадлежащих (a;b), выполняется
(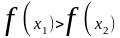 ).
).
Теорема 1.
Для
того чтобы функция
,
дифференцируемая на (a;b), была возрастающей,
необходимо, чтобы производная на этом
промежутке была неотрицательна, т.е.
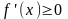 ,
и достаточно, чтобы
,
и достаточно, чтобы
 .
.
Теорема 2.
Для
того чтобы функция
,
дифференцируемая на (a;b), была убывающей,
необходимо, чтобы производная на этом
промежутке
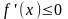 и достаточно, чтобы
и достаточно, чтобы
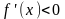 .
.
Пример:
Найти интервалы возрастания и убывания
функции
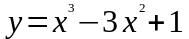 .
.
 .
.
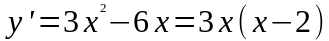
![]() .
.
 .
.
