13.Нечеткие выводы: алгоритм Sugeno.

Нечетким логическим выводом называется получение заключения в виде нечеткого множества, соответствующего текущим значениях входов, с использованием нечеткой базы знаний и нечетких операций.

Предполагается, что в заключении высказывания имеется математическое выражение для вычисления значений z: zi=F(xi,yi)

Пусть в базе правил имеется 2 правила вида:

П1: Если х есть А1, у есть В1, то z=a1*x+b1*y

П2: Если х есть А2, у есть В2, то z=a2*x+b2*y

где a и b - некоторые числа.

База знаний Сугено аналогична базе знаний Мамдани за исключением заключений правил, которые задаются не нечеткими термами, а линейной функцией от входов. Правила в базе знаний Сугено являются своего рода переключателями с одного линейного закона "входы - выход" на другой, тоже линейный. Границы подобластей размытые, следовательно, одновременно могут выполняться несколько линейных законов, но с различными степенями.

1. Этап нечеткости: определяются степени истинности, т.е. значения функций принадлежности для левых частей каждого правила (предпосылок). Для базы правил с m правилами обозначим степени истинности как

A1(x0) B1(y0)

A2(x0) B2(y0)

2. Находятся уровни отсечения:

И индивидуальные выводы каждого из правил:

3. Четкое значение выхода всей системы:

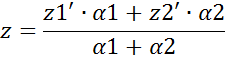
14. Нечеткие выводы: алгоритм Larsen.

В алгоритме Larsen нечеткая импликация моделируется с использованием оператора умножения.

Описание алгоритма:

1. Этап нечеткости: определяются степени истинности, т.е. значения функций принадлежности для левых частей каждого правила (предпосылок). Для базы правил с m правилами обозначим степени истинности как

A1(x0) B1(y0)

A2(x0) B2(y0)

2. Как и в Мамдани используются операторы отсечения:

А потом операция отсечения с помощью операции умножения:

3. Находится итоговое нечеткое подмножество с функцией принадлежности:

4. При необходимости производится приведение к четкости.

15.Нечеткие выводы: упрощенный алгоритм нечеткого вывода.

Исходные правила в данном случае задаются в виде:

где с1 и с2- обычные четкие числа.

Описание алгоритма:

1. Этап нечеткости: определяются степени истинности, т.е. значения функций принадлежности для левых частей каждого правила (предпосылок). Для базы правил с m правилами обозначим степени истинности как

A1(x0) B1(y0)

A2(x0) B2(y0)

2. На втором этапе находятся числа по Сугено:

3. На 3-ем этапе находится четкое значение выходной переменной по формуле:

16. Нисходящие нечеткие выводы.

Рассмотренные до сих пор нечеткие выводы представляют собой восходящие выводы от предпосылок к заключению. В последние годы в динамических нечетких системах начинают применяться нисходящие нечеткие выводы.

Пример: возьмем упрощенную модель диагностики неисправности автомобиля с именами переменных Х=[ Х1, Х2, Х3] У=[ У1, У2 ]:

Х1- обработка машинного масла

Х2 – затруднение при запуске

У1 – ухудшение цвета выхлопных газов

У2 – недостаток мощности.

Между переменными Хi и Yi существуют нечеткие причинные отношения, которые можно представить в виде некоторой матрицы с элементами R_ij принадлежащими [0;1]. Конкретные предпосылки и заключения можно рассмотреть как нечеткие множества Х и У. Отношения этих множеств можно обозначить следующим образом:

У=X◦R

В данном случае направление выводов является обратным направлением вывода. выходы В (симптомы) определяют входы А(факторы).

Матрица R- знания эксперта:

	y1	y2
x1	0.9	0.6
x2	0.1	0.5
x3	0.2	0.5

Результат осмотра: Х= 0,9/х1+0,1/х2+0,2/х3=[0.9;0.1;0.2]

У=X◦R = 0.9/y1+0.6/y2.

Т.е. можно сделать вывод, что, скорее всего, неисправен аккумулятор.

На практике в подобных задачах могут одновременно использоваться различные композиции нечетких выводов. Сама схема выводов может быть многокаскадной. Общих методов решения подобных задач не существует. Операции суммирования и умножения заменяются на операции объединения и пересечения.