10.Свойства нечетких отношений.

Бинарное нечеткое отношение, заданное на декартовом произведении X*X(X*Y).

1. Рефлексивность:

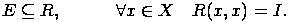
Все элементы главной диагонали матрицы рефлексивного бинарного н/о равны 1.

2. Слабая рефлексивность:

3. Сильная рефлексивность:

4. Антирефлексивность:

Все элементы главной диагонали матрицы антирефлексивного бинарного н/о равны 0.

5. Слабая антирефлексивность:

6. Сильная антирефлексивность:

7. Симметричность:

Матрица симметричного бинарного н/о симметрична относительно главной диагонали.

8.Антисимм.:

(min)

Для выполнения этого свойства требуется лишь, чтобы один из двух (а может быть и оба) симметричных относительно главной диагонали элементов матрицы соответствующего бинарного н/о был равен 0

8. Асимметричность:

9. Сильная линейность:

11. Слабая линейность:

12.Транзитивность:

(max min)

13. Котранзитивность:

11.Нечеткие выводы: алгоритм Mamdani.

Нечетким логическим выводом называется получение заключения в виде нечеткого множества, соответствующего текущим значениям входов, с использованием нечеткой базы знаний и нечетких операций.Пусть в базе правил имеется m правил вида:

R₁: ЕСЛИ x₁ это A₁₁ … И … x_n это A_1n, ТО y это B₁

R_i: ЕСЛИ x₁ это A_i1 … И … x_n это A_in, ТО y это B_i

R_m: ЕСЛИ x₁ это A_i1 … И … x_n это A_mn, ТО y это B_m,

где x_k , k=1..n – входные переменные; y – выходная переменная; A_ik – заданные нечеткие множества с функциями принадлежности.

Результатом нечеткого вывода является четкое значение переменной y^* на основе заданных четких значений x_k , k=1..n.

Механизм Мамдани наиболее распространенный способ логического вывода в нечетких системах. В нем используется минимаксная композиция нечетких множеств. Данный механизм включает в себя следующую последовательность действий.

1. Этап нечеткости: определяются степени истинности, т.е. значения функций принадлежности для левых частей каждого правила (предпосылок). Для базы правил с m правилами обозначим степени истинности как A_ik(x_k), i=1..m, k=1..n.

2. Этап Нечеткий вывод. Сначала определяются уровни "отсечения" для левой части каждого из правил:

Далее находятся "усеченные" функции принадлежности:

3. Композиция, или объединение полученных усеченных функций, для чего используется максимальная композиция нечетких множеств: где µ(y) – функция принадлежности итогового нечеткого множества.

4. Дефазификация, или приведение к четкости. Существует несколько методов дефазификации. Например, метод среднего центра, или центроидный метод:

Геометрический смысл такого значения – центр тяжести для кривой MF(y). Рисунок 6 графически показывает процесс нечеткого вывода

по Мамдани для двух входных переменных и двух нечетких правил R1 и R2.

12. Нечеткие выводы: алгоритм Tsukamoto.

Нечетким логическим выводом называется получение заключения в виде нечеткого множества, соответствующего текущим значениях входов, с использованием нечеткой базы знаний и нечетких операций.

В данном алгоритме предполагается, что ф-ии принадлежности для заключений высказывания являются монотонными.

Пусть даны нечеткие высказывания в след форме

Пi:Если X есть Ai, Y есть Bi, то Z есть Сi.

Пусть n=2. При конкретных входных значениях x0, у0. Определены выходные четкие значения z0

1. Этап нечеткости: определяются степени истинности, т.е. значения функций принадлежности для левых частей каждого правила (предпосылок). Для базы правил с m правилами обозначим степени истинности как

A1(x0) B1(y0)

A2(x0) B2(y0)

2. Находят усечение ф-ии принадлежности для заключения нечетких правил.

Нах min значение для предпосылок каждой строки нечетких правил

2. Нах значение z1 и z2 для соотв. ф-ии принадлежности, посредством решения правил:

4. Получение четкого значения центроидным методом