1.Нечеткие множества.

Нечеткое мн. – это такое мн., элементы которого входят в данное мн. с той или иной степенью вероятности. Пусть X – мн. принадлежащее E – универсальное мн. R – некоторое свойство. Обычное четкое подмножество А – универсального подмножества Е, элементы которого удовлетворяют свойству R, определяется как множество упорядоченных пар.

А = {μ_А(Х) / Х}

μ_А(Х) – характеристическая функция и для четкого подмножества А принимает значение 1, если Х удовлетворяет свойству R и 0 в ином случае.

Нечеткое подмножество отличается от обычного тем, что для Х (принадлежащего Е) нет однозначного ответа «да» или «нет» относительно свойства R. В связи с этим нечеткое подмножество A определяется таким же образом как и для четкого множества, но функция μ_А(Х) в этом выражении будет называться характеристической, которая принимает значения от 0 до 1. Множество М называется множеством принадлежностей. Функция принадлежности указывает степень принадлежности Х к множеству А. Если M = {0, 1}, то такое множество может рассматриваться как обычное четкое.

Ex Примеры записи нечетких множеств:

1. E={x₁,x₂,x₃,x₄,x₅} М=[0..1]

μ_А(x₁)=0.5 μ_А(x₂)=0.3 μ_А(x₃)=1 μ_А(x₄)=0 μ_А(x₅)=0.1

2. A={0.5/ x₁,0.3/x₂,1/x₃,0/x₄,0.1/x₅}

3. A={0.5/ x₁+0.3/x₂+1/x₃+0/x₄+0.1/x₅} неарифметическое сложение

2.Основные характеристики нечетких множеств.

Нечеткое множество – это такое множество, элементы которого входят в данное множество с той или иной степенью вероятности.

Пусть M = [0,1] и A - нечеткое множество с элементами из универсального множества E и множеством принадлежностей M.

Носителем (суппортом) нечёткого множества supp A называется множество

Эта величина называется высотой нечёткого множества A. Нечёткое множество A нормально, если его высота равна 1. Если высота строго меньше 1, нечёткое множество называется субнормальным.

Нечёткое множество пусто, если .

Непустое субнормальное нечёткое множество можно нормализовать по формуле:

Немодальное нечеткое мн. – такое мн., для которого , только для одного эл. x из универсального множества E.

Носитель нечеткого множества – обычное четкое подмножество, для которого выполняется μ_А(Х)>0.

Точки перехода нечеткого множества – такие элементы универсального множества E, для которых μ_А(Х)=0,5.

Ex Примеры нечетких множеств:

1. E={0,1,2,3,4,5,6}

“несколько”={0/0+0.3/1+0.9/2+1/.+0.7/4+0.3/5+0/6}

характеристиками являются: sup μ_А(Х) = 1

носителями являются: 1,2,3,4,5

точка перехода: -

2. E={0,1..∞} М=[0..1] Задание с пом ф-ии:

“мало”={ μ_А(Х) = 1/(1+(n/10)²)}

3. E={0,1..100} Задание с пом систем:

μ_{молодой}(Х)=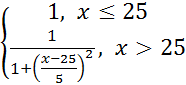

3.Логические операции над нечеткими множествами.

При М=[0,1]. Пусть A и B - нечеткие множества на универсальном множестве E.

1. Включение AcB

A содержится в B, если для любых x принадлежащих E выполняется:

μ_А(x) ≤ μ_B(x).

2. Равенство A=B

A и B равны, если для любых x принадлежащих E выполняется:

μ_А(x) = μ_B(x).

3. Дополнение A=¬B

A и B дополняют друг друга, если для любых x принадлежащих E выполняется: μ_А(x) = 1- μ_B(x).

В данном случае определено для М=[0,1], но можно и на любом другом диапазоне упорядоченных значений М.

4. Пересечение A∩B

5. Объединение AUB

6. Разность A-B= A∩¬B μ_A-B= min(μ_A(x) 1 - μ_B(x))

7. Дизъюнктивная сумма

μ_A(+)B= max{[min{ μ_A(x), 1 - μ_B(x)}, min{1 - μ_A(x), μ_B(x) }] }

Рассмотрим прямоугольную систему координат, по оси у – значения характеристической функции μ_А(x), а по оси х – в произвольном порядке расположены эл-ты унив. мн. Е.

Свойства:

1. Коммутативность

2. Ассоциативность

,

3. Идемпотентности

4. Дистрибутивность

,

5. 

6. Закон Де Моргана

,

7. 

4.Алгебраические операции над нечеткими множествами.

1. Произведение A·B

2. Сумма A+̂B

3. Возведение в степень, на основе опер алгебр произв

Частные случаи:

1. A²=CON A, при возведении в степень >1, эфф. концентрир.

2. DIL A = A^0.5, степень <1, эффект растяжения нечеткого мн.

4. Умножение на число α

5. Оператор увеличения нечеткости

Используется для преобразования ч/м в н/м и для увеличения нечеткости н/м. A – н/м. Для х определены н/м К(х), совокупность их –ядро оператора увеличения нечеткости(Φ). Результатом действия оператора Φ на н/м А является н/м вида:

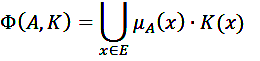
6. Четкое подмножество α-уровня у/м E

Свойства:

1. Коммутативность

2. Ассоциативность

3. з-н де Моргана

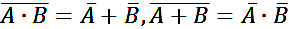
4. Идемпотентность

5. Дистрибутивность

6. 

Свойства совместного использования:

1. 

2. 

5.Нечеткая и лингвистическая переменные.

Используются при описании объектов и явлений при помощи нечетких множеств.

Нечеткая переменная характеризуется <α, X, A> -

α – наименование нечеткой переменной,

Х – универсальное множество,

А – нечеткое множество на Х, описывающее ограничение с помощью характеристической функции μ_А(x).

Лингвистической переменной называется набор <β, T, X, M, G>

β – наименование лингвистической переменной

T – множество значений, представляющее собой наименование нечетких переменных, область определения которых Х. Множество T называют базовым террамножеством множеством лингвистической переменной

G – это синтаксическая процедура, позволяющая оперировать элементами мн. T, в частности, получать новые термы.

TVG(T) – расширенной террамножество.

М – это семантическая процедура, позволяющая превратить каждое новое значение лингвистической переменной, образуемое процедурой G, в нечеткую переменную, т.е. сформировать соответствующее нечеткое множество. Нечеткие множества для термов G(t) задаются в соответствии с правилами.

Лингвистическая переменная это множество нечетких переменных, она используется для того чтобы дать словесное описание некотоpомy нечеткому числу, полyченномy в pезyльтате некоторых операций. Т. е. путем некоторых операций подбирается ближайшее по значению из лингвистической переменной.

Ex Толщина изготовленного изделия [10..80]

β – толщина изделия

T – “малая”,”средняя”,”большая”

X=[10..80]

G – “средняя и малая”,”очень малая”