Проявления волн Россби на земле
Из проявлений волн Россби на нашей планете рассмотрим — синоптические вихри в океанах, открытые советскими исследователями [14]. При их интерпретации необходимо учесть неоднородность плотности океана по вертикали (обусловленную зависимостью плотности от температуры, давления и концентрации растворенных в воде солей). Но эта неоднородность влечет за собой необходимость учета волнового движения не только по горизонтали, но и по вертикали. Учет вертикального волнового движения в волнах Россби приводит к интересному результату: дисперсионное уравнение для волн структурно остается тем же самым, но в качестве характерного размера дисперсии входит уже не радиус Россби — Обухова (8) (он называется баротропным), а так называемый внутренний (или бароклинный) радиус Россби:
(16)
где N — частота Брента — Вяйсяля вертикальных колебаний неоднородной жидкости, устойчивой по отношению к конвекции (плотность жидкости убывает по вертикали). В несжимаемой среде
(17)
учет
сжимаемости приводит к появлению в
скобках (17) второго слагаемого, равного
,
где
—
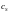скорость звука в среде; т
— номер вертикальной моды в верхнем
слое океана. В условиях океана, при
,
величина
км (много меньшая, чем величина
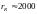км) оказывается весьма близкой к размерам
наблюдаемых синоптических вихрей, а
скорость их дрейфа (на запад), имеющая
порядок нескольких см/с, приблизительно
соответствует скорости Россби
(но
никак не
,
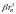что отвечало бы вертикально однородной
среде). Поэтому синоптические вихри в
океанах рассматриваются как бароклинные
волны Россби. Они именно потому умещаются
в океанах, что их размеры определяются
величиной
км, а не величиной
км. Другой пример аналогичной закономерности
— природный атмосферный вихрь в Большом
Красном Пятне Юпитера (см. п. 2.2) и глубинные
(внутренние бароклинные) антициклонические
вихри («линзы») размером
в океанах Земли.
Рассмотрим формирование стоячего планетарного вихря вследствие остановки волны Россби ветром, дующим ей навстречу [4, 15, 16]. Пусть волна Россби распространяется в среде, которая сама движется относительно планеты со скоростью и (положительное направление этой скорости — на восток). Если без движения среды (т. е. в отсутствие ветра) атмосфера была однородной, то наличие ветра сделает ее неоднородной: на ветер действует сила Кориолиса, пропорциональная fu, которая вызывает уравновешивающий ее градиент гидростатического давления (2):
Теперь скорость волны Россби относительно ветра определяется соотношениями (6) и (11), а скорость волны относительно планеты составит
Видно, что если скорость ветра удовлетворяет условию
то
волна Россби, при отсутствии ветра
распространявшаяся на запад, под влиянием
встречного ветра остановится. В условиях
Земли указанное равенство для волны
длиной
км может установиться при скорости
ветра в несколько м/с. Теперь учтем, что
волна Россби достаточно большой амплитуды
обладает свойствами вихря: она сохраняет
«свои» частицы и не пропускает внутрь
себя посторонние. При этом, после того
как выльются «свои» осадки, в районе
локализации вихря Россби могут наблюдаться
застойные явления типа длительной
засухи (например, такой, которая была в
нашей стране в 1972 г.). Это так называемые
блокинги [15]. Если скорость ветра превышает
указанную выше величину, то волна Россби
сносится (встречным) ветром на восток.
Для очень длинных волн Россби (
,
)
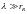влияние ветра на скорость их распространения
исчезает: снос волны ветром в точности
компенсируется увеличением скорости
волны относительно ветра под влиянием
возникшего градиента гидростатического
давления. По этой причине солитон Россби
не сносится ветром (течением) [17].