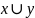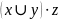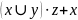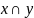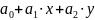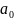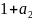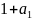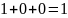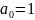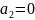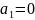Математический анализ
1.
Найти предел
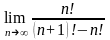 .
.
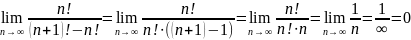
2. Найти предел .
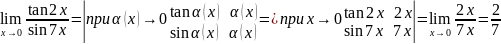
3.
Исследовать функцию на непрерывность
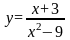 .
.
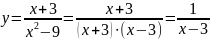
Знаменатель функции обращается в ноль при х=3. Исследуем ф-ю на непрерывность в этой точке:
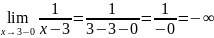
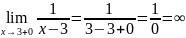
В точке х=3 функция терпит неустранимый разрыв второго рода
4.
Найти производную функции
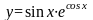 .
.
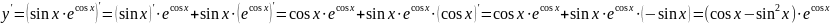
5. Найти частные производные второго порядка по всем переменным функции
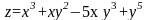 .
.
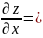
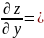
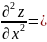
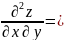
6.
Исследовать функцию на экстремум, найти
точки перегиба и интервалы выпуклости
и вогнутости её графика
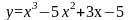 .
.
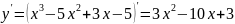
Найдем точки подозрительные на экстремум:
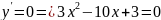
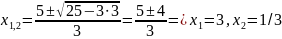
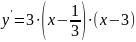

y(х)
возрастает при х
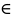 (-∞;1/3)
(-∞;1/3)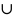 (3;∞)
, убывает при х
(1/3; 3)
(3;∞)
, убывает при х
(1/3; 3)
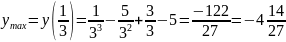
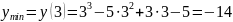
Найдем точки перегиба:
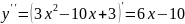
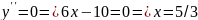
y (x)
вогнута при х
(5/3 ;
(x)
вогнута при х
(5/3 ;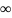 )
, выпукла при х
(-∞; 5/3)
)
, выпукла при х
(-∞; 5/3)
х=5/3 точка перегиба
7.
Найти интеграл
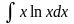 .
.
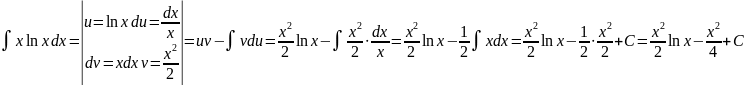
8.
Вычислить площадь фигуры, ограниченной
линиями
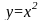 и
и
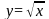 .
.

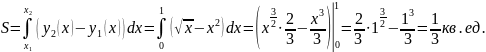
Ответ:
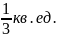
9 .
Вычислить интеграл
.
Вычислить интеграл
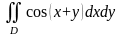 ,
где D - область, ограниченная
прямыми
,
где D - область, ограниченная
прямыми
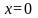 ,
,
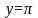 ,
,
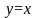 .
.
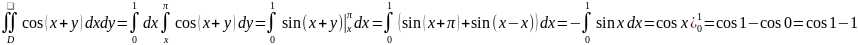
Ответ: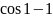
10.
Вычислить криволинейный интеграл
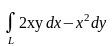 ,
где L - дуга параболы
от точки (0;0) до точки (1;1).
,
где L - дуга параболы
от точки (0;0) до точки (1;1).
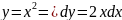
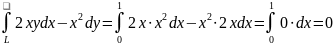
11.
Исследовать ряд на сходимость
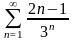 .
.
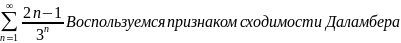
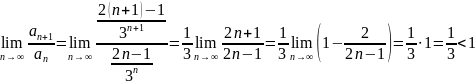
следовательно
ряд
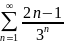 сходится
сходится
Ответ: сходится
12.
Найти область сходимости ряда
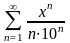 .
.
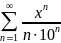
Воспользуемся признаком сходимости Даламбера:
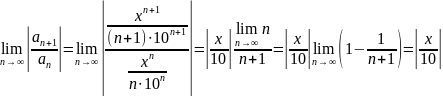
Требуем,
чтобы
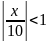 , следовательно
, следовательно
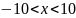
Исследуем сходимость на границах интервала:
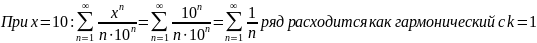
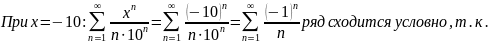
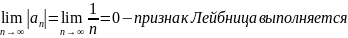
Ответ:
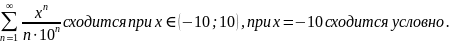
13. Исследовать ряд на абсолютную и
условную сходимость
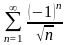 .
.
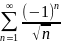
Проверим выполнение признака Лейбница:
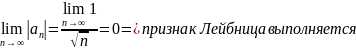
Следовательно ряд сходится условно, исследуем абсолютную сходимость:
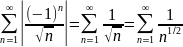 ряд расходится как обобщенный
гармонический с k=1/2 <1
ряд расходится как обобщенный
гармонический с k=1/2 <1
следовательно абсолютная сходимость не выполняется
Ответ: сходится условно
Комплексный анализ
14.
Вычислить
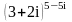 ,
явно выделив действительную и мнимую
части.
,
явно выделив действительную и мнимую
части.
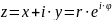
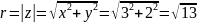
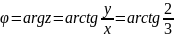
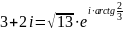
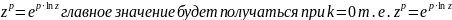
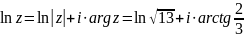
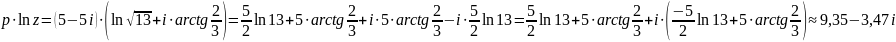
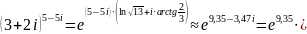
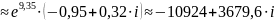
15.
Разложить в ряд Лорана функцию
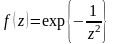
Точка z=0 является особой точкой функции, других особых точек функция не имеет. Ряд Лорана для данной функции будет только один и сходиться он будет в области |z|>0.
В
известном разложении
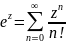 заменяем z на –1/z2
и получаем
заменяем z на –1/z2
и получаем
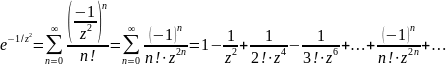
Дискретная математика
21.
Найти СКНФ булевой функции
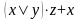
Составим таблицу истинности функции:
x |
y |
z |
|
|
|
0 0 0 0 1 1 1 1 |
0 0 1 1 0 0 1 1 |
0 1 0 1 0 1 0 1 |
0 0 1 1 1 1 1 1 |
0 0 0 1 0 1 0 1 |
0 0 0 1 1 0 1 0 |
Для построения СКНФ по таблице истинности выбираются наборы, приводящие функцию в значение ноль. Переменная записывается с инверсией, если равна 1 в этом наборе.
СКНФ:
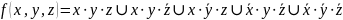
22.
Докажите, что функция
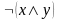 не
является линейной?
не
является линейной?
Функция f(x1,…,xn) называется линейной, если существует a0,a1,…,an B такие, что
f(x1,…,xn)=a0+a1×x1+…+an×xn.
Тогда
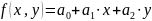
x |
y |
|
|
|
следствие |
0 0 1 1 |
0 1 0 1 |
0 0 0 1 |
1 1 1 0 |
|
противоречие |
Получили противоречие, значит функция нелинейна
23. Дана матрица смежности 6-вершинного графа.
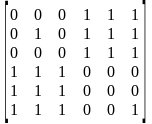
Является ли он планарным?
Изобразим граф

По формуле Эйлера для плоского графа справедливо: |V(G)| – |E(G)| + |F(G)| = 2
Отсюда F(G)=2+11-6=7
Без петель F(G)=5 , E(G)=9
Любая
грань (включая внешнюю) содержит четное
число ребер – а значит , не менее 4.
Поскольку каждое ребро включается в
ровно две грани, получается
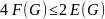 .
.
Соотношение не выполняется, значит его нельзя расположить на плоскости, т.е. граф не является планарным