2.2. Необходимые и достаточные условия подобия

Теорема: достаточным условием подобия двух систем является равенство любых двух соответствующих критериев подобия этих систем, составленных из их основных параметров и начальных (граничных) условий.

Теорема указывает, каковы должны быть системы, чтобы между ними существовало подобие.

Чтобы создаваемая машина или имитируемое явление были подобны модели, нужно:

1) выбрать s определяющих параметров, включая в них начальные (граничные) условия и, если необходимо, время, и составить из них s – r независимых критериев подобия;

2) выбрать параметры натуры так, чтобы ее критерии были такие же, как у модели: , .

Причем условие принято выражать так:

П_k = idem

(idem означает такой же, одно и то же).

Выполненным выше операци­ям можно дать следующее толкование: примем некото­рую систему за модель и выберем ее параметры М, L, Т в качестве первичных величин, благодаря чему получим основные единицы [М], [L], [Т].

Тогда числовое значение относящихся к натуре вели­чин можно получить, измерив все соответствующие вели­чины модели в системе единиц [mM], [lL], [tT]; в таком случае модель и натура подобны. Действительно,

, ,

.

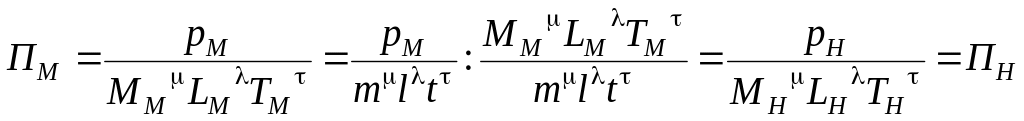Отсюда видно, что при выборе на основе модели зна­чений для величин натуры произвольные значения можно придать лишь стольким величинам натуры, сколько имеется основных единиц измерения (точнее – каков ранг матрицы).

Предположим теперь, что подобие между системами имеется заведомо. Каковы в таком случае необходимые условия подобия?

Здесь возможны два случая.

1. Рассмотрим теперь системы, в которых, каждому значению q_i соответствует только один набор параметров р_к, т. е. связь между обоб­щенными координатами и параметрами взаимно одно­значная.

Поскольку подобие между моделью и натурой заведомо имеет место, для сходственных моментов вре­мени (для сходственных точек пространства) справедли­во соотношение

, .

Теперь поставим такую задачу: выполнить еще одну модель, подобную натуре, с тем же коэффициентом подобия

,

(штрихом помечаем величины, относящиеся ко второй модели). В таком случае все соответствующие критерии подобия второй модели и натуры будут равны (обеспечиваем при создании второй модели достаточные условия их подобия).

Кроме того, имеем:

,

, .

Но поскольку то, ввиду отмеченной однозначности,

,

т. е. в нашем случае, при подобии модели и натуры соот­ветствующие критерии модели и натуры равны.

2. Если одному и тому же значению q_i могут соответ­ствовать различные наборы параметров p_к, то в общем случае при подобии не все критерии модели и натуры равны. Например, если П₁ = sin П₂, то равенство П_1М = П_1Н возможно при

,

Отметим, что рассмотренный случай встречается сравнительно редко, но его все же следует иметь в виду.

Таким образом: Необходимым условием подобия двух систем является равенство соответствующих критериев подобия этих систем, составленных из обобщенных коорди­нат и параметров систем.

Если достаточные условия накладывают определенные ограничения на параметры систем, обусловливая этим их подобие, то необходимые условия позволяют установить связь между координатами и параметрами систем.

2.3. П – теорема

Теорема теории подобия, извест­ная под названием П-теоремы, формулируется следующим образом: функциональная зависимость между характеризующими процесс величинами может быть представлена в виде зависимости между составленными из них критериями подобия.

Использование теоремы дает известные преимущества при экспериментальном исследовании. Применяя безраз­мерные комплексы величин, полученные результаты мож­но распространить на все подобные процессы и уменьшить число величин, которые следует связать функциональной зависимостью. Действительно, в этом случае вместо n+s величин имеем n+s–3 безразмерных комплексов, и на­хождение зависимости между ними упрощается. Особен­но легко находится эта зависимость, если критериев всего два; тогда для определения вида функции П₁=f(П₂) достаточно сравнительно небольшого числа измерений.

Пусть, например, требуется исследовать движение ма­тематического маятника. Характеризующие маятник величины: период Т, длина нити l, ускорение свободного падения g, максимальный угол отклонения нити от вер­тикали  (в радианах). Из этих величин можно составить два безразмерных комплекса:  и .

Следовательно (), откуда (),

где Ф – некоторая функция максималь­ного угла отклонения .

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

Пример выполнения задания №1.

Задача 1. Груз массой т (рис. 1, а) колеблется на пружине жесткости С в вязкой среде, сила сопротивления F_k = – к. На груз действует возмущающая сила F₀sint. Перемещение груза х является функцией этих величин и времени:

x = f (m, k, , F₀, с, t). (1)

а)	б)	в)
Рис. 1 Колебания: а) колебания с демпфированием подвешенного к пружине груза; б) амплитудно-частотная характеристика в безразмерных координатах; в) электрический колебательный контур

Решение 1:

Имеющиеся п вели­чин р₁, р₂, р₃, …, р_п, характеризующих процесс, дают п – r критериев подобия

П = с … , (2)

где r – ранг матрицы (3 – 4), – размерность величины р_i :

.

Числа z₁, z₂, ..., z_n таковы, что размерность П равна нулю. Величины z₁, z₂, ..., z_n находятся путем решения системы уравнений:

(3)

Система имеет п – r линейно независимых решений. Каждое решение, состоящее из п значений z_i, дает один критерий подобия. Таким образом, необходимо решить систему (3). Степени размерностей , , для каждой величины указаны в таблице 1 (в данном случае p₁ = m, р₂ = с, p₃ = x, p₄ = t, p₅ =F₀, p₆ = , p₇ = k).

Ранг матрицы, составленной на основе таблицы 1 равен трем.

Таблица 1.

Величина		Степени
p1 р2 p3 p4 p5 p6 p7	m с x t F0  k	1 = 0 2 = 0 3 = 0 4 = 0 5 = 0 6 = 0 7 = 0	1 = 1 2 = 1 3 = 0 4 = 0 5 = 1 6 = 0 7 = 1	1 = 0 2 = – 2 3 = 0 4 = 1 5 = – 2 6 = – 1 7 = – 1

Система уравнений (3) примет вид

(4)

Число величин, характеризующих процесс, п = 7, ранг матрицы r = 3, поэтому система (4) имеет п – r = 4 линей­но независимых решений. При нахождении этих решений; четыре величины z_i (4 независимых решения!) имеют произвольные значения, остальные три величины на­ходятся из (4). Это означает, что в (2) четыре значения z_i выбираются произвольно, а остальные три такие, что критерий П является безразмерной величиной, т. е. остальные три значения «компенсируют» размерность, обусловленную выбором первых четырех величин. Произ­вол в выборе некоторых чисел z не имеет никакого значения, важно лишь одно – чтобы величина П была безраз­мерной. Поэтому выбираем наиболее простые значения, причем для тех z, для которых это возможно по уравне­ниям (4) – например, дать произвольные значения для z₁, z₂, z₃, z₇ нельзя, поскольку в таком случае первое и второе уравнения системы (4) противоречат друг другу.

1. Принимаем

z₁ = 1, z₂ = z₆ = z₇ = 0

Тогда

z₃ + z₅ = 0, 1 + z₅ = 0, z₄ – 2 z₅ = 0

откуда

z₅ = – 1, z₃ = 1, z₄ = – 2

Итак, первое решение:

z₁ = 1, z₂ = 0, z₃ = 1, z₄ = – 2, z₅ = – 1, z₆ = 0, z₇ = 0.

2. Принимаем

z₁ = 0, z₂ = 1, z₆ = z₇ = 0.

Тогда из (4)

z₃ + z₅ = 0, 1 + z₅ = 0, – 2 + z₄ – 2 z₅ = 0,

откуда

z₅ = – 1, z₃ = 1, z₄ = 0.

Итак, второе решение:

z₁ = z₂ = 0, z₃ = 1, z₄ = 0, z₅ = – 1, z₆ = z₇ = 0.

3. Принимаем

z₁ = z₂ = 0, z₆ = 1, z₇ = 0.

Тогда из (4)

z₃ + z₅ = 0, z₅ = 0, z₄ – 2 z₅ – 1= 0,

откуда

z₅ = 0, z₃ = 0, z₄ = 1.

Следовательно, третье решение:

z₁ = z₂ = z₃ = 0, z₄ = 1, z₅ = 0, z₆ = 1, z₇ = 0.

4. Принимаем

z₁ = z₂ = z₆ = 0, z₇ = 1.

Тогда из (4)

z₃ + z₅ = 0, z₅ + 1 = 0, z₄ – 2 z₅ – 1 = 0,

откуда

z₅ = – 1, z₃ = 1, z₄ = – 1.

Поэтому четвертое решение:

z₁ = z₂ = 0, z₃ = 1, z₄ = – 1, z₅ = 1, z₆ = 0, z₇ = 1.

Таким образом, получено четыре решения, которым соответствуют четыре независимых критерия подобия.

Из первого решения получаем критерий

,

.

Из второго решения

,

Из третьего решения

.

Из четвертого решения

, .

Решение 2:

Критерии подобия можно получить и несколько иным способом, используя ту же последовательность, которая применена для доказательства достаточного условия по­добия (метод нулевых размерностей). Так, выбрав какие-либо три параметра (по числу первоначальных основных единиц – метр, килограмм, секунда), для которых опре­делитель , можно в соотношении (1) перейти к безразмерным величинам. Такими параметрами могут быть т, , F₀,

, , .

Для них

.

Уравнение (1) можно выразить так:

. (5)

Значения , , определяем из условия, что входящие в (5) комплексы – безразмерные величины:

1)

, откуда ;

, откуда

, откуда ,

, .

2)

; , откуда

, откуда ,

.

3)

; , , .

4) .

Из полученных результатов видно, что четыре критерия соответствуют четырем критериям .

ЗАДАНИЕ №1

0. Найти критерии подобия и установить их взаимосвязь для случая истечения сыпучего материала из отверстия. Рассмотрим идеализированный случай, считая, что слипание частиц и внутреннее трение отсутствуют. Тогда параметрами процесса являются: Q – расход сыпучего материала, кг/сек; D – диаметр отверстия, м; d – средний размер зерна, м;  – плотность, кг/м³; g – ускорение свободного падения. Расход материала Q является функцией остальных параметров.

0. Найти критерии подобия и установить их взаимосвязь при определении силы сопротивления, действующую на тело заданной формы, движущееся с некоторой скоростью в вязкой тяжелой жидкости, имеющей свободную поверхность. Величину силы определяют следующие величины: v – скорость тела, м/сек;  – плотность жидкости, кг/м³; ν – кинематическая вязкость, м²/сек; l – некоторый характерный размер, м; g – ускорение свободного падения, м/сек².

0. Найти критерии подобия и установить их взаимосвязь при определении силы сопротивления, действующую на тело заданной формы, движущееся с некоторой скоростью в вязкой тяжелой жидкости, имеющей свободную поверхность. Величину силы определяют следующие величины: v – скорость тела, м/сек;  – плотность жидкости, кг/м³; v – кинематическая вязкость, м²/сек; l – некоторый характерный размер, м; g – ускорение свободного падения, м/сек²:

0. Рабочий процесс вентилятора определяют следующие величины: плотность среды , кг/м³, число оборотов в единицу времени п, 1/сек; диаметр винта D, м; расход воздуха Q, м^г/сек; напор Н, н/м² и мощность N, вт. Определить критерии подобия.

0. Рабочий процесс поршневой машины определяется следующими величинами: мощность, N, Вт, среднее давление газа, p_ср, МПа; l – длина хода; D, м – диаметр; n – число оборотов вала кривошипа в минуту. Определить критерии подобия.

0. Жидкость, которую можно считать несжимаемой, истекает из круглого отверстия радиусом r, м в среду с давлением P, МПа. Коэффициент расхода μ. Давление полного торможения в среде, из которой истекает жидкость равно P*, МПа. Определить критерии подобия.

0. Определить напряжения во вращающемся диске постоянной толщины. Наружный радиус диска, r₁, м; радиус отверстия, r₂, м; коэффициент Пуассона, μ; удельный вес, ; ускорение свободного падения, g; число оборотов, n; расстояние от центра до точки, где определяется напряжение, l; компоненты напряжений σ_r и σ_t.

0. Определить силу сопротивления действующую на тело заданной формы, движущееся с некоторой скоростью в вязкой тяжелой жидкости, имеющей свободную поверхность. При движении происходит обмен теплом между телом и жидкостью. Скорость тела , м/с; плотность жидкости , кг/м³; кинематическая вязкость , м²/с; характерный размер l, м; ускорение свободного падения g, м/сек²; количество теплоты Q, Дж; теплоемкость жидкости с, Дж/ кгК; температура жидкости T, К.

0. Рабочий процесс вентилятора авиационного двигателя определяют следующие величины: плотность среды , кг/м³, число оборотов в единицу времени п, 1/сек; диаметр миделевого сечения D, м; расход воздуха G, м^г/сек; давление за вентилятором p, н/м²; мощность N, Вт; высота полета H, м; скорость полета , м/с; температура окружающей среды на заданной высоте T, К. Определить критерии подобия.

0. Рабочий процесс свободной турбины ГТУ определяют следующие величины: плотность среды , кг/м³, число оборотов в единицу времени п, 1/сек; диаметр D, м; расход продуктов сгорания G, м^г/сек; давление за свободной турбиной p, н/м²; мощность N, Вт; температура продуктов сгорания на входе в турбину T, К; сила тока на генераторе I, А. Определить критерии подобия.

Пример выполнения задания №2.

Задача 1. Необходимо опытным путем определить распределение тем­ператур в длинном стальном вале диаметром d = 400 мм через τ = 2,5 ч после загрузки его в печь.

Для стали коэффициенты теплопроводности и температуропроводности равны соответственно λ=42 Вт/(м°С), a=1,18 10^-5 м²/с. Коэффициент теплоотдачи к валу в печи α = 116 Вт/(м²°С).

Исследование решено проводить в небольшой печи на геометрически подобной модели вала, выполненной из легированной ста­ли. Для модели λ _м = 16 Вт/(м°С); а_м = 0,5310^-5 м²/с; α_м = 150 Вт/(м²°С);

Определять диаметр d_м модели вала и промежуток времени, через который после загрузки модели в печь необходимо измерить распределение температур в модели,

Решение:

Подобие температурных полей вала и модели будет иметь место при равенстве критериев для образца и модели:

и .

Критерии Био и Фурье для вала

;

.

Из условия находим диаметр модели вала:

м.

Из условия находим искомый промежуток времени:

с.

Задача 2. На паропроводе перегретого пара диаметром d =400 мм установлена измерительная диафрагма, которая должна быть спе­циально протарирована, т. е. должна быть найдена зависимость Δр =f (G), где Δр – перепад статических давлений в диафрагме, Па; G – расход пара, кг/с.

Так как по производственным причинам тарировка не могла быть произведена непосредственно на образце, то для этой цели была изготовлена модель в 1/5 натуральной величины.

В результате испытаний модели на воде, температура которой t_{ж м} = 20°С, были получены значения перепадов давлений на диа­фрагме при различных расходах воды. Результаты измерений при­ведены ниже:

Δр, Па	477	1178	4520	18 050	72 200
G, кг/с	2,22	4,44	8,88	17,76	35,52

Найти зависимость Δр =f (G) для образца при течении пара в автомодельной области и указать границы ее применения. Давле­ние пара р=98 кПа. Температура пара t_ж=250°С.

Решение:

Произведем обработку опытных данных в критериях подобия и построим зависимость Eu =f (Re). Эта зависимость будет действи­тельна и для пара. Поэтому по полученной для модели зависимости Eu =f (Re) можно найти зависимость Δр =f (G) для случая течения пара в образце.

Для определения зависимости Eu =f (Re) подсчитываем значения критериев для опытных данных тарировки на модели.

Критерий Эйлера

Eu .

Учитывая, что скорость

,

получим

Eu .

При t_{ж м} = 20°С для воды =998 кг/м³; = l10^-6 м²/с.

Подставляя известные величины, находим:

Eu .

Критерий Рейнольдса

Re ,

где

м.

Подставляя значения G_м и Δр_м , полученные при тарировке диа­фрагмы» подсчитаем соответствующие значения критериев подобия. Результаты этих расчетов представлены в следующей таблице:

Δрм, Па	Gм, кг/с	Wм, м/с	Eu	Re
477 1178 4520 18 050 72 200	2,22 4,44 8,88 17,76 35,52	0,443 0,886 1,772 3,544 7,088	2,44 1,505 1,44 1,44 1,44	35 400 70 800 141 600 283 200 566 400

По этим данным построим кривую зависимости Eu =f (Re).

Из таблицы и графика ясно, что при Re > 1,4210⁵ Eu = const = 1,44 наблюдается автомодельная область. Следовательно, при течении пара через образец при Re>1,4210⁵ критерий Eu = 1,44. Воспользуемся этим соотношением для нахождения искомой зависимости. Для образца при течении пара

Euω²= ,

где при р = 98 кПа и t_ж = 250°С удельный объем  = 2,452 м³/кг.

Заменяя скорость через расход

,

где расход G, кг/с, получаем:

,

откуда

при Re > 1,4210⁵.

Задача 3. На воздушной модели парового котла, выполненной в масштабе 1/8 натуральной величины, производилось изучение теплоотда­чи конвекцией. Для первого газохода модели при различных скоро­стях воздуха были получены следующие значения коэффициента теп­лоотдачи:

Wм, м/с	2,0	3,14	4,65	8,8
αм, Вт/м2С	50,4	68,6	90,6	141

Средняя температура воздуха, проходящего через модель, t_{ж м} = 20°С. Диаметр трубок модели d_м = 12,5 мм. Коэффициент тепло­отдачи α_м при обработке опытных данных был отнесен к средней арифметической разности температур между жидкостью и стенкой. На основе данных, полученных на модели, найти формулу для расчета теплоотдачи конвекцией в 1-м газоходе котла в виде зависи­мости Nu = f (Re).

Решение:

По данным, полученным на модели, зависимость для теплоотда­чи ищем в виде Nu = CReⁿ.

Число Nu_м и число Re_м ,

где при t_{ж м} = 20°С для воздуха λ_ж = 0,026 Вт/(м  °С) и = 15,0610^-6 м²/с.

Подставив соответствующие значения в выражения для чисел Nu и Re, получим:

Nu_м = 0,481 и Re_м = 830 ,

Результаты вычисления чисел Nu_м и Re_м для соответствующих значений и сведены в таблицу:

ωм, м/с	αм, Вт/м2С	Reм	Nuм
2,0 3,14 4,65 8,8	50,4 68,6 90,6 141	1660 2600 3860 7300	24,2 33,0 43,6 68,0

По этим данным строим зависимость Nu_м = f (Re_м) в логарифмических координатах (см. рис.). По тангенсу угла наклона кривой к оси абсцисс определяем показа­тель степени п, а затем постоян­ную С: C=Nu_м/Re_мⁿ. Получаем расчетную формулу Nu = 0,15Re^0,685, действительную в пределах 1 600  Re  7 300.

ЗАДАНИЕ №2

0. Определить значения чисел Nu, Re, Gr, Eu, Pe для следующих условий: среда движется по трубе диаметром 24х2 мм и длиной 2 м, ее расход 50 кг/ч. На входе температура среды 80 °С, на выходе 40 °С, средняя температура стенки трубы 25 °С. Сопротивление движению среды 400 Па. В качестве среды принять воду и воздух. Определяющие параметры – средняя температура среды и внутренний диаметр трубы.

1. Азот при температуре 200 °С и абсолютном давлении 10⁶ Па движется в трубе со скоростью 10 м/с. Для исследования гидродинамического процесса построена уменьшенная в 4 раза модель, где движется вода с температурой 20 °С. Определить скорость воды в модели.

2. Температурное поле в длинном цилиндре диаметром 200 м исследуется по истечении 30 и 60 мин с помощью модели. Теплопроводность и температуропроводность материала цилиндра 15 Вт/(мК) и 2010^-4 м²/с, материала модели 4 Вт/(мК) и 810^-4 м²/с. Найти диаметр модели и время, когда в модели следует измерять распределение температур. Принять коэффициент теплоотдачи для цилиндра 9,8 и для модели 35 Вт/(м²К).

3. Найти кинематическую вязкость для жидкости в модели, где изучается теплообмен при вынужденной конвекции, если коэффициент температуропроводности жидкости 0,810^-6 м²/с. В образце в виде трубы движется воздух с температурой 180С и абсолютным давлением 10⁵ Па.

4. Модель вала изготовлена из материала с теплопроводностью 27,2 Вт/(мК), теплоемкостью 4 кДж/(кгК) и плотностью 510 кг/м³. Модель помещена в нагреватель. После 22,4 мин нагрева производится измерение температур в модели, по этим замерам определяется распределение температур в образце – стальном вале – после 2 ч нагрева его в печи. Стальной вал имеет диаметр 400 мм, температуропроводность 1110^-6 м²/с, а коэффициент теплоотдачи в печи 110 Вт/(м²К). Найти диаметр модели и коэффициент теплоотдачи в нагревателе.

5. Шар диаметром 0,4 м с температурой 600 °С должен охлаждаться в масляной ванне, где поддерживается температура 100С. Распределение температуры в шаре после охлаждения в течение 10 мин должно быть изучено на бетонной модели диаметром 0,6 м, которая после разогрева до 110С охлаждаемся в воздухе с температурой 10С. Через сколько минут следует начать измерение температур в модели? Определить соотношение температур в образце и модели в сходственных точках. Температуропроводность материала шара 13,310^-6, бетона 5,010^-6 м²/с.

6. Для измерения расхода газа в трубопровод диаметром 270 мм поставили диафрагму. Ее размеры были определены после испытаний на модели, уменьшенной в 3 раза. Во время испытаний через модель пропускалась вода с температурой 30С, при расходе воды более 28 м³/ч наблюдался автомодельный режим. Найти минимальный расход газа для автомодельного режима, а также соответствующие этому расходу скорость газа и гидравлическое сопротивление (сопротивление на модели составило 280 мм. рт. ст.). Принять плотность газа 0,9 кг/м³, кинематическую вязкость 1410^-6 м²/с.

7. Теплоотдача в газоходе котла исследовалась на модели в 1/4 натуральной величины. При этом были получены коэффициенты теплоотдачи при различных скоростях воздуха, представленные ниже:

α, Вт/(м2К)	42	76	138
, м/с	4	8	16

Наружный диаметр труб модели 14 мм, на стенке трубы темпера­тура 30°С, Воздух имел температуру 70С при 1,01310⁵ Па. По дан­ным испытаний на модели получить формулу Nu_п.cd = CRe_п.cdⁿ и указать пределы ее применимости по Re, Используя полученную фор­мулу, найти для натурного газохода тепловой поток, передаваемый дымовыми газами стенкам труб, если газы движутся со скоростью Ю м/с и имеют на выходе 800°С, на входе 1О00Х. Температура сте­нок труб 300°С, поверхность нагрева 600 м². Состав дымового газа: , , .

8. При изучении теплообмена на модели в условиях естествен­ной конвекции между горизонтальной трубой с температурой t_С и воз­духом получены следующие данные:

tС, С	85	125	145
α, Вт/(м2К)	9,34	10,35	10,76

Труба наружным диаметром 45 мм была помещена в воздух с тем­пературой 20°С. По измерениям на модели найти обобщенную зависи­мость в виде формулы Nu_жd = C(Gr Pr)_ж.dⁿ, используя которую, опре­делить теплоту, передаваемую за 5 ч от горизонтальной трубы диа­метром 10 мм и длиной 4 м к воде с температурой 40°С. Температура поверхности трубы равна 60 °С.

9. На воздушной модели котла производилось изучение тепло­отдачи при вынужденной конвекции, и при различных скоростях воз­духа были получены представленные ниже коэффициенты теплоотдачи:

α, Вт/(м2К)	50,5	68,6	90,7	141,2
, м/с	2,0	3,14	4,65	8,8

В модели средняя температура воздуха 20°С, трубы имеют диаметр 14 мм. По данным, полученным на модели необходимо определить значения С и п в формуле Nu_жd = CRe_ж.dⁿ. Используя полученную формулу, найти поверхность нагрева натурного котла, если скорость дымовых газов в газоходе 8 м/с, а средняя температура газов 800°С. Трубы диаметром 80 мм имеют на поверхности температуру 300°С. Переда­ваемый тепловой поток 1,2 МВт. Состав дымовых газов: , , .