2. Основные теоремы теории подобия.

2.1. Понятие подобия

Обозначим словом система совокупность физических объектов (элементов системы), объединенных на основе некоторого признака, индивидуализирующего набор данных элементов и сообщающего системе определенные качества. Будем иметь в виду такие системы, состояние которых является однозначной функцией состояний отдельных элементов.

Параметрами системы назовем величины, характеризующие ее элементы и воздействующие на нее внешние объекты, т.е. величины, выделяющие каждый объект из множества других той же физической природы; обобщенные координаты системы — величины, описывающие поведение системы — их количество равно числу степеней свободы системы.

Обобщенные координаты могут изменяться с течением времени, или от точки к точке. Например, для системы: груз массой m, колеблющийся на пружине жесткости с при ускорении свободного падения g, обобщенной координатой, является отсчитываемое от некоторого начального положения вертикальное смещение груза х, параметры m, g, с. Из множества параметров данной системы выделим минимально возможное количество параметров, достаточное для однозначного определения состояния системы; эти параметры между собой независимы, назовем их основными, или определяющими.

Пусть имеются две системы одинаковой физической природы, состоящие из одинакового числа аналогичных элементов, которые играют в обеих системах одинаковую роль. Одну систему назовем модель, другую систему — натура, относящиеся к ним величины обозначим соответственно индексами м, н.

Система определяется s независимыми (основными) параметрами p_k и имеет п независимых обобщенных координат . Время и начальные условия включим в число параметров и условимся, что индекс i имеет значения 1, 2, ..., п, а индекс k — значения п+1, ..., n + s.

Обобщенные координаты этих систем являются одинаковыми функциями параметров:

.

Вообще ; .

Две системы называют подобными, если их любые две соответствующие обобщенные координаты для любых сходственных моментов времени (сходственных точек пространства) пропорциональны, т. е. две системы подобны, если

,

где q_сi = const, t_н = t_ct_М, t_c = const, t_н, t_M – сходственные моменты времени.

Таким образом, если известно, что две системы подобны и можно найти коэффициенты подобия q_сi , то, зная поведение одной системы (модели), можно знать и то, как будет вести себя другая система (натура).

Примером подобия систем может служить один из наиболее простых, но часто встречающихся на практике случаев. Две механические системы, для любых двух соответствующих точек которых справедливы равенства

, , ,

очевидно, будут подобными (такие системы называют еще кинематически подобными). В данном случае обобщенными координатами являются, декартовы, коэффициенты подобия для всех координат одинаковы.

Если между точками систем существует еще материальное подобие, т.е. , то системы называют динамически подобными. При наличии динамического подобия легко устанавливается связь между всеми кинематическими и динамическими характеристиками систем. Так, для скоростей характерна связь

;

аналогично

;

для ускорений

;

для сил

;

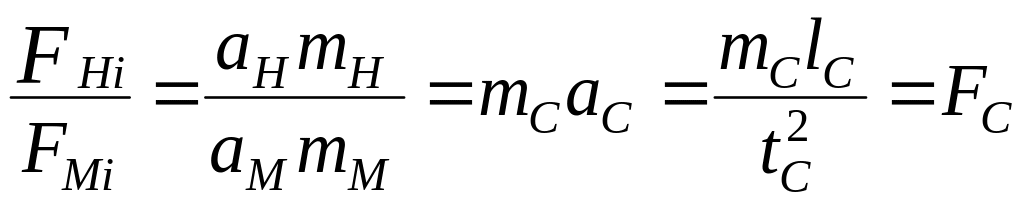и так далее.

При динамическом подобии систем коэффициенты подобия различных величин выражаются через исходные коэффициенты подобия т_С , l_с, t_c – при помощи формул размерности этих величин:

; ;

; .

Часто коэффициенты подобия одних вторичных величин удобно выражать через коэффициенты подобия других вторичных величин. Например,

.

Если же плотность соответствующих частей обеих систем одинакова, т.е.

,

то и .