5.6 Сурет. Марковтың тізбегі кейіпіндегі дереккөз (бірінші қадам).
Анықтама 5.3.5. Соңғы дискретті r жадты марковтық дереккөз толықтай келесі шарттармен анықталады:
1.
Бос емес
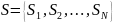ахуалдар көпшілігі берілген, сонымен
бірге,
S ұзындық r векторын қамтамасыз етеді;
2.
Әрбір Si
ахуалы
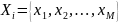алфавитті және р(і)(j)
алфавитінің j-
типті символды ықтималдықты дискретті жадсыз дереккөзге сәйкес;
3.
r
– 1 ретті
символды
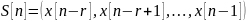ахуалы
және
келесі x[n]
символы
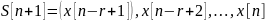
жаңа ахуалын құрады;
4. Ахуалдардың бастапқы бөліп таралуы берліген
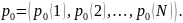
Біз r жады r ретті символдарды қамтамасыз ететінін байқаймыз, себебі келесі символдың ықтималдығына дәл алдыңғы r символдар ықпал етеді. Мұны толықтай мысалда қарастырайық.
5.4. Стационарлы марковтық дереккөздің энтропиясы
Стационарлы марковтық дереккөздің энтропиясы дереккөздің әрбір ахуалы белгілі бір энергияға ие жадсыз кіші дереккөз болып табылады деген түсініктен шығып есептеледі. Осылайша, әуелгі дереккөздің энтропиясы кіші дереккөздердің энтропиясының математикалық күтіміне тең.
Теорема 5.4.1. N ахуалға, яғни әрқайсысының энтропиясы төмендегідей N кіші дереккөзге ие М символды алфавиті бар стационарлы марковтық дереккөз
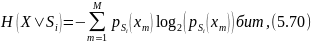
кіші дереккөздердің энтропиясының математикалық күтіміне тең энтропияға ие
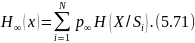
Алдағыда эвристикалық амал (5.71), 5.1.1 бекітудегі стационарлы дискретті дереккөздің энтропиясының жалпы қасиетіне сәйкес екендігі көрсетіледі.
Ескерту. Бекітудің дәлелі дерліктей қиын, сондықтан оны келесі бөлімдерді түсінуге зақымсыз жіберуге болады.
Дәлел. Марковтық дереккөздің энтропиясы [10].
Дәлел үш қадамда келтіріледі.
Қадам 1.
Бірінші
қадамда мағлұм
ахуалда марковтық дереккөздің шартты
энтропиясы келесі түрде анықталатынын
көрсетеміз
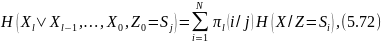
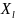арқылы
l-ші
кіші дереккөз белгіленген, ал
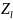арқылы
l-ші
қадамдағы ахуал.
(5.72)
дәлелдеу үшін, энтропияның негізінде
жатқан шартты
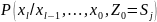ықтималдықтарды
қарап шығамыз және түрлендіреміз.
Кейінгі шектеу ретінде Zl
ахуалын енгіземіз
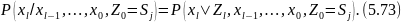
Zl
толықтай
бастапқы Z0
ахуалымен
және
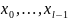символдарымен
анықталатындықтан, қосымша шектеулер
шартты ықтималдыққа ықпал етпейді, яғни
теңдік әділетті. Екінші түрлендіру l-ші
символ l-ші
ахуалға тәуелді болатын марковтық
дереккөздің шамаланған қасиетінен
шығады.
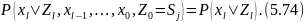
Шартты (5.72) энтропияны табу үшін энтропияның негізінде жатқан шартты ықтималдықтарды сәйкес ықтималдықтарға көбейту қажет және математикалық күтімді табу керек
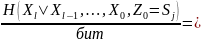
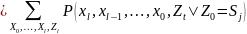
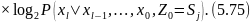
Zl шамалары бірлескен ықтималдықтарға ықпал етпейді, себебі барлық Zl ахуалдарға соманы бөліп тарату шекті болып табылады.
Сол жағын (5.74) ескере отырып, алатынымыз
Берілген Z0 және Sj-лерде l-ші уақыт қадамында Xl символының ықтималды-ғы Si ахуалында xl символы берілген шарттағы Si-дегі Sj ықтималдығына тең
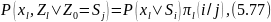
сондықтан, (5.76) үшін біз жаза аламыз
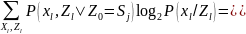
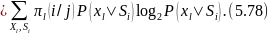
Берілген Si ахуалды барлық Xl символдар бойынша сома і-ші кіші дереккөздің энтропиясына тең
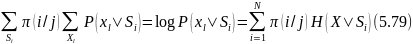
және (5.72) бекіту дәлелденді.
Қадам 2.
Осы уақытқа дейін біз назарға алынған бастапқы ахуалдан шықтық. Марковтық дереккөздің энтропиясын математикалық күтім арқылы анықтау үшін бастапқы ахуалды кездейсоқ деп есептейміз
j бойынша сумма барлық i-ші ахуалдарға өтуді қамтиды, ол нәтижесінде l-ші қадамда і-ші ахуалдың ықтималдығын береді. Дереккөздің стационарлығын ескере отырып, аламыз
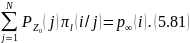
Соңында шығатыны
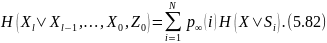
Стационарлы марковтық дереккөздің шартты энтропиясы l символдар санына тәуелді емес. (5.82) және (5.71) теңдіктердің бірінші бөліктері біркелкі. Енді қалатыны (5.82) және (5.71)-лердің сол жақ бөліктерінің тең екенін l → ∞ тұсында дәлелдеу.
Қадам 3.
Энтропия үшін өрнекті мағлұм бастапқы ахуал тұсында қарап шығайық және оны «тізбек қағидасы» арқылы түрлендіреміз
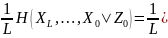
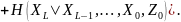
Марковтық дереккөз стационарлы болғандықтан, оң жақтың барлық қиысулары тең және (5.82)-ге сәйкес анықталады. Егер L қиысу болса, кез-келген натурал L үшін алатынымыз
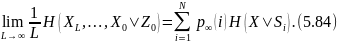
Сол жақтағы шарт әлі бұзылмаған. Универсалды қатынасты пайдаланып
Алатынмыз
(5.84)-тен шығады
Сонымен қатар, универсалды қатынасты пайдаланып
Аламыз
Энтропия үшін бағалау орынды
демек
және шекті жағдайда алатынымыз
Стационарлы марковтық дереккөз үшін (5.87)-ден (5.92)-ні қолданып нақты (5.71)-ді аламыз.