4.1. Өзара және шартты ақпарат

Ақпараттар теориясын аксиоматикалық құрылуы кезінде жұп оқиғалар ақпараты деген түсінік қолданылған. Бұл пайымдауларды еске алайық және жалпылайық. Екі дискретті X және Y дереккөздерді қарастырайық. Олардың оқиғаларын жұп оқиғаларға (x_i, y_i) біріктірейік. Сонда біз байланысты дереккөздердің қарапайым моделін аламыз(4.1 сурет).

4.1 Сурет. Екі байланысты дереккөздің моделі.

Егер екі дереккөз қандай-да бір тәсілмен өзара байланысты болса, онда бір дереккөздің оқиғасы басқа дереккөздің оқиғасы жайлы біршама болжам жасауға мүмкіндік береді. Ақпараттар теориясында бұл термин екінші дереккөздің анықталмағандығы төмендейтінін білдіреді, яғни дереккөздер өзара ақпарат алмасады.

Шартты p(x/y) ықтималдығын енгіземіз – x оқиғасының ықтималдығы y оқиғасы орындалған шартта. Екі x_i және y_i оқиғаларының өзара p(x_i, y_i) ықтималдығын олардың априорлы және шартты ықтималдықтары арқылы жүзеге асырамыз

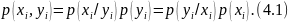
Логарифмдік функцияны қолданып, (x_i, y_i), (x_i) және (y_i) оқиғаларының ақпараттарын аламыз

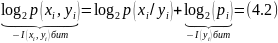
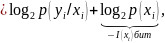
яғни

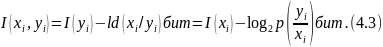
(4.3)-тің екінші бөлігінде I(y_i)-ті және, сәйкес, бірінші бөлігінде I(x_i)-ті қосып және сол уақытта алып тастасақ

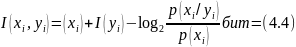
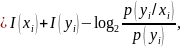
Осылайша, жұп оқиғалар (x_i, y_i) ақпараты бұл оқиғалардың анықталмағандығын төмендететін кейбір теріс емес шамаларын алып тастап ақпараттарының қосындысы арқылы анықталады, яғни өзі ақпарат болып табылады. Сол себепті оны жұп оқиғалардың өзара ақпараты деп атаймыз.

Жұп оқиғалардың өзара ақпараты келесі түрде анықталады

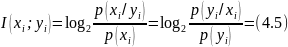
Өзара I(x_i; y_i) ақпараты әр уақытта оң екеніне назар аударайық. Өзара ақпараттың дереккөздерге қатысты симметриясы да маңызды қасиет болып табылады, себебі

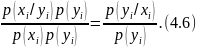
(4.5)-тегі дереккөздерге қатысты симметрия дереккөздер арасындағы ақпарат алмасу біртараптық емес өзара екендігін дәлелдейді.

Өзара ақпараттың мәнін түсіну үшін, екі жақын жағдайды қарап шығайық.

1. Дереккөздер тәуелсіз. Онда екі тәуелсіз жұп оқиғалар үшін

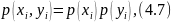
яғни дереккөздер ақпарат алмаспайды

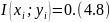
2. Дереккөздер берік байланысқан, яғни бір дереккөздің оқиғасы басқа дереккөздің оқиғасын анықтайды

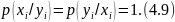
Бұл жағдайда толық ақпарат алмасу жүзеге асады

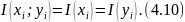
(4.4) бойынша, (х_і, у_і) жұп оқиғаларының ақпаратын тәуелсіз I(х_і) + I(у_і) жұп оқиғаларының ақпараттары арасындағы айырмашылық және Х және У дереккөздерінің байланысына тәуелді, алдын ала болжам қылынған I(х_і, у_і) өзара ақпараты деп түсінуге болады

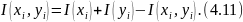
Және бір мәрте (4.3)-ті қарап шығайық және шартты ақпарат түсінігін енгізейік.

Шартты ақпарат (апостериорлы белгісіздік)

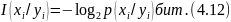
(4.3) бойынша

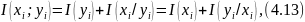
яғни жұп оқиғалар ақпаратын у_і оқиғасы мағлұм болғандағы у_і және х_і оқиғаларының ақпараттарының қосындысы я болмаса х_і оқиғасы мәлім болғандағы х_і және у_і оқиғаларының ақпараттарының қосындысы деп анықтауға болады.

4.2. Бірлескен және шартты энтропия

Алдыңғы бөлімде жеке жұп оқиғаларды қарап шыққан соң дереккөздердің орташа бағасына өтейік.

4.2 суретте қазіргі жағдай көрсетілген

А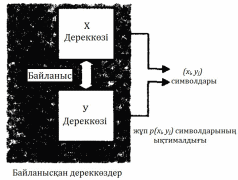 лфавит Х = {x_i, … , x_M}

Ықтималдық p(x_i)

Шартты ықтималдық p(y_j, x_i)

және p(x_i, y_j)

Алфавит Y={y_j, … , y_N}

Ықтималдық p(y_j)