АҚПАРАТ,

ЭНТРОПИЯ ЖӘНЕ

ШЫҒЫН

2.1. Бір оқиғаның ақпараты

Ақпарат алмасу, өзінің материалды емес табиғатына қарамастан, біздің өміріміздің ажыралмас бөлігі болып табылады. Заманауи ақпараттар теориясының негізін қалаушылардың бірі, Норберт Виннер, ақпаратты келесі түрде сипаттады [9]:

“Ақпарат ол материя да емес, энергия да емес, ақпарат ол ақпарат”.

Н. Виннердің пікірінше, ақпарат ол материя және энергия секілді жаңа бір элемент. Ақпарат түсінігі ғылыми түрде қаншалықты күрделі болса, адамзат үшін ақпарат соншалықты маңызды. Біз қандай-да бір дербес оқиғаны мысалға ала отырып: “Бұл мағлұматтың мен үшін маңызы зор” - деп айтамыз. Мұндай субъективті көзқарас ақпараттың техникалық сипаттамасына тура келмейді.

Қатаң ғылыми түсінік болғандықтан, ақпарат техникаға өлшенетін шама ретінде енгізілуі қажет(ұзындықтағы метрге, кернеудегі вольтқа ұқсас).

Біздің күнделікті тәжірибеміз ақпаратты қабылдаған уақытта біз әрдайым қандай-да бір белгісіздікті айқындайтынымызды көрсетеді. Бұл кездейсоқ оқиғалармен тәжірибені еске түсіреді. Мұндай тәжірибелерді өткізіп біз кездейсоқ оқиғаларды бақылаймыз және бұл жүйенің беймағлұмдығын төмендетеді.

Енді ақпараттық теорияның өзіндік мазмұнына өтеміз. Әуелі, қарапайым дереккөздің сипаттамасын берейік, онан соң оның жәрдемімен дереккөзді суреттеу үшін өлшенетін шама ретінде ақпарат саны түсінігін енгіземіз.

Жадсыз дискретті дереккөз

Жәй Х жадсыз дискретті дереккөзі уақыттың әр назар салынған сәтінде

P(x_i) = p_i ықтималдықпен P(x_i) = {х₁, х₂, ... , х_N} ақырғы алфавитінен х_і символын береді. Символ талғау бір бірінен тәуелсіз мәртебеде өтеді.

Қарапайым мысал ретінде Х = {x₁ = 0, x₂ = 1} алфавитті және 0 ≤ р₁ ≤ 1 һәм р₂ = 1 – p₁ ықтималдықты екілік жадсыз дереккөзді келтіруге болады. Келесі сан талғауы бастапқы немесе соңғы таңдаулардан тәуелсіз түрде өтеді. Қарапайым дереккөздің бейнесі 2.1 суретте көрсетілген. Әуелі біріңғай оқиғаларды қарастырайық. Күнделікті тәжірибеміздің нәтижесі жиі орын алатын оқиғалар және олардың ықтималдықтары бізге аз мағлұмат беретінін көрсетеді. Мысал үшін “Ит иесін тістеп алды” деген хабарламаны алайық. Бұл үйреншікті жағдайды барлық газеттер үлкен шрифтпен жазса да оған ешкім назар аудармас еді. Бұдан келесі қорытынды шығаруға болады: жиі болатын оқиғалар өзімен аз мағлұмат алып жүреді және керісінше сирек яғни күтілмеген оқиғаларда көп мағлұмат болады. Демек ақпарат және ықтималдық бір-біріне теріс пропорционалды түрде тәуелді. Мұнан шыға, келесі үш аксиома негізінде өлшенетін шама ретінде ақпарат саны деген түсінік енгіземіз [1].

2.1 Сурет. Қарапайым х алфавитінің ақпарат дереккөзі.

Ақпарат санын анықтауға арналған аксиомалар [1]

1. Жалғыз x₁ Є X оқиғасының р_і ықтималдығымен болған ақпараты оң мәнге ие

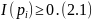
2. Екі тәуелсіз (x_i , x_j) оқиғаларының бірлескен ақпараты бірлескен P(x_i, х_j) = р_ij = р_i ∙ р_j ықтималдығымен олардық ақпараттарының қосындысына тең

3. Ақпарат оқиға ықтималдығынан үзілмес функция болып табылады.

1 және 2 аксиомалардың тұжырымдамасы бірнеше оқиғаның ақпараты өзара жойыла алмайтындығын көрсетеді. 2 аксиома оқиғаның бірлескен ақпараты түсінігін енгізеді. 3 аксиоманың бойынша оқиға ықтималдығындағы өзгеріс оның мағлұматының да өзгеруіне әкеліп соғады. 2 аксиома екі тәуелсіз оқиғаның ақпаратын анықтайды. Оқиға ақпараты оның ықтималдығының логарифмдік функциясы ретінде анықталатынын (2.2) білеміз. Демек, ақпаратты келесі жолмен анықтай аламыз:

Р ықтималдықпен болып жатқан оқиғаның ақпараты, тең болады

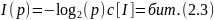
Бұл формулада екілік логарифм қолданылған. Екілік логарифм келесі сипаттарда да берілуі ықтимал: log₂(x) = ld (x) = lb(x) , ld дегені дуальды лоагрифм термині, lb – бинарлы. Кейде нат бірлік шамалы натуралды логарифмді қолданады, бірақ ақпараттың кез-келген өлшем бірлігін де қолдануға болады. Сонымен қатар есептеу формуласын қолданып бір бірліктен екіншісіне өтуге де мүмкіндік бар:

.

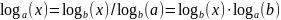Бит өлшемі ақпараттық техникада екілік есептеу системасында қолданылады. Келесі тарауларда суреттелетіндей, кез-келген сұраққа екі ғана жауабы бар шешім қабылдау процессін сипаттауда екілік система өте қолайлы: “иә” және “жоқ”. “Бит” түсінігінің көрнекі интерпретациясы [10]-да көрсетілген.