2 Задача

По 20 предприятиям региона изучается зависимость выработки продукции на одного работника (тыс. руб.) y от ввода в действие новых основных фондов (% от стоимости фондов на конец года) x₁ и от удельного веса рабочих высокой квалификации в общей численности рабочих (%) х₂.

Необходимо:

1. Рассчитать параметры линейной многофакторной модели. Пояснить экономический смысл полученных коэффициентов.

2. Оценить качество модели в целом. Сделать соответствующие выводы.

3. Оценить целесообразность включения в модель фактора x₁ после х₂ и х₂ после х₁.

4. Дать сравнительную характеристику влияния факторов на результат.

5. Оценить статистическую значимость коэффициентов регрессии.

6. Предполагая прогнозные значения переменных равными х₁=7 и х₂=26, найти с вероятностью 0,95 дать интервальную оценку индивидуального прогнозного значения выработки продукции на одного работника.

Решение:

1. Расчет параметров линейной многофакторной модели. Для расчета параметров используем метод наименьших квадратов. Суть данного метода состоит в построении и решении системы нормальных уравнений.

Д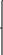 анная система имеет вид:

∑ y = na +b₁∑x₁ +b₂∑x₂

∑ yx₁ = a∑x₁ +b₁∑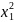 + b₂∑x₁x₂

∑yx₂ = a∑x₂ +b₁∑x₁x₂ +b₂∑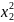

n=20 – количество наблюдений

Для удобства проведения расчетов поместим результаты промежуточных расчетов в таблицу 1.

Таблица 1

№	y	x1	x2	yx1	yx2	x1x2			y2
1	7,0	3,9	10,0	27,3	70,0	39,0	15,21	100,0	49,0
2	7,0	3,9	14,0	27,3	98,0	54,6	15,21	196,0	49,0
3	7,0	3,7	15,0	25,9	105,0	55,5	13,69	225,0	49,0
4	7,0	4,0	16,0	28,0	112,0	64,0	16,0	256,0	49,0
5	7,0	3,8	17,0	26,6	119,0	64,6	14,44	289,0	49,0
6	7,0	4,8	19,0	33,6	133,0	91,2	23,04	361,0	49,0
7	8,0	5,4	19,0	43,2	152,0	102,6	29,16	361,0	64,0
8	8,0	4,4	20,0	35,2	160,0	88,0	19,36	400,0	64,0
9	8,0	5,3	20,0	42,4	160,0	106,0	28,09	400,0	64,0
10	10,0	6,8	20,0	68,0	200,0	136,0	46,24	400,0	100,0
11	9,0	6,0	21,0	54,0	189,0	126,0	36,0	441,0	81,0
12	11,0	6,4	22,0	70,4	242,0	140,8	40,96	484,0	121,0
13	9,0	6,8	22,0	61,2	198,0	149,6	46,24	484,0	81,0
14	11,0	7,2	25,0	79,2	275,0	180,0	51,84	625,0	121,0
15	12,0	8,0	28,0	96,0	336,0	224,0	64,0	784,0	144,0
16	12,0	8,2	29,0	98,4	348,0	237,8	67,24	841,0	144,0
17	12,0	8,1	30,0	97,2	360,0	243,0	65,61	900,0	144,0
18	12,0	8,5	31,0	102,0	372,0	263,5	72,25	961,0	144,0
19	14,0	9,6	32,0	134,4	448,0	307,2	92,16	1024,0	196,0
20	14,0	9,0	36,0	126,0	504,0	324,0	81,0	1296,0	196,0
∑	192	123,8	446	1276,3	4581	2997,4	837,74	10828,0	1958,0
Ср. знач.	9,6	6,19	22,3	63,815	229,05	149,87	41,887	541,4	97,9

Найдем средние квадратические отклонения признаков:

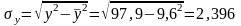
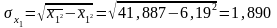
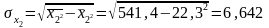
Для нахождения параметров линейного уравнения множественной регрессии

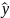= a + b₁x₁ + b₂x₂

Необходимо решить систему линейных уравнений относительно неизвестных параметров a,b₁,b₂.

∆ = =

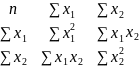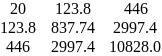
∆ = 20∙(837,4∙10828 – 2997,4∙2997,4) – 123,8∙(123,8∙10828 – 2997,4∙446) + 446∙(123,8∙2997,4 – 837,74∙446) = 139940

∆ a = =

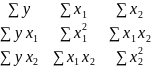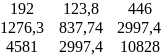
∆ a = 192∙(837,74∙10828 – 2997,4∙2997,4) – 1276,3∙(123,8∙10828 – 2997,4∙446) + 4581∙(123,8∙2997,4 – 837,74∙446) = 256833

∆b₁ = =

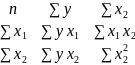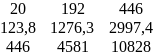
∆b₁ = 20∙(1276,3∙10828 - 4581∙2997,4) – 123,8∙(192∙10828 - 4581∙446) + 446∙(192∙2997,4 – 1276,3∙446) = 132376

∆ b₂ = =

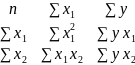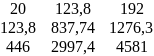
∆b₂ = 20∙(837,74∙4581 – 2997,4∙1276,3) – 123,8∙(123,8∙4581 – 2997,4∙192) +446∙(123,8∙1276,3 – 837,74∙192) = 11981,36

a =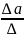 = 1,835; b₁ = 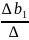= 0,946; b₂ = 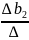= 0,0856.

Таким образом, получили следующее уравнение множественной регрессии:

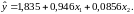
Вывод: Уравнение регрессии показывает, что с увеличением ввода в действие новых основных фондов на 1% (у) выработка продукции на одного работника увеличивается на 0,946 тыс. руб. при фиксированном значении фактора х₂. С увеличением х₂ удельного веса работников высокой квалификации на 1% (у) выработка продукции возрастет на 0,0856 тыс. руб. при фиксированном значении х₁.

2) Оценка качества модели в целом. Для оценки состоятельности сегодня используют критерий Фишера, который рассчитывается по формуле:

F = ∙ ,

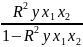где R² – коэффициент детерминации; n – количество наблюдений; m – количество зависимых переменных.

Рассчитаем сначала парные коэффициенты корреляции:

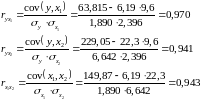
Коэффициент множественной корреляции определить через матрицы парных коэффициентов корреляции:

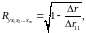где

∆ r =

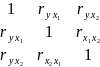
- определитель матрицы парных коэффициентов корреляции;

∆r₁₁ =

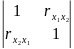
• определитель матрицы межфакторной корреляции.

Находим:

∆ r = 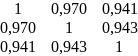= 1+0,8607+0,8067-0,8855-0,8892-0,9409 = 0,0058

∆r = 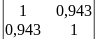=1- 0,8892 = 0,1108.

Коэффициент множественной корреляции:

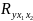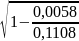= = 0,973

Коэффициент множественной корреляции указывает на весьма сильную связь всего набора факторов с результатом.

Коэффициентом множественной детерминации R² называется квадрат множественного коэффициента корреляции.

Нескорректированный коэффициент множественной детерминации 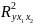= 0,947.

В нашем случае фактическое значение критерия Фишера:

F_факт = 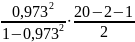=151,88.

Табличное значение данного критерия при уровне значимости α = 0,05 (α = 1 – р = 1 – 0,95) и в степенях свободы k₁ = m=2 (количество факторов) и k₂ = n – m – 1 = 20 – 2 – 1= 17 составляет 3,59.

Вывод: Поскольку полученное расчетное значение F_факт = 151,88 превышает табличное, то модель считается состоятельной и пригодной для составления прогноза.

3) При оценке целесообразности включения в модель фактора х₁ после х₂ и фактора х₂ после х₁ используем частный критерий Фишера:

= ∙ ; = ∙ .

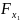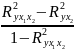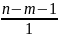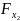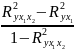Найдем 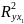и :

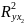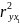= = 0,970² = 0,941;

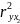= = 0,941² = 0,885.

Имеем:

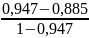= ∙ =19,89;

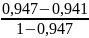= ∙ = 1,924.

Табличное значение данного критерия при уровне значимости α = 0,05 и степенях свободы к₁ = 1 и к₂ = 17 составит 4,45.

Вывод: F_x1>4.45, следовательно, фактор х₁ целесообразно включать в модель после введения фактора х₂. F_x2<4.45, следовательно, фактор х₂ не целесообразно включать в модель после введения фактора х₁.

4) Сравнительная характеристика влияния факторов на результат.

Для сравнительной характеристики воспользуемся средним коэффициентом эластичности:

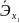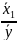= b₁ ∙ = 0,946 ∙ 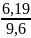= 0,61;

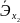= b₂ ∙ 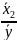= 0,0856 ∙ 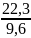= 0,2.

Вывод по фактору х₁: С увеличением фактора х₁ на 1% выработка продукции возрастет на 0,61%.

Вывод по фактору х₂: С увеличением фактора х₂ на 1% выработка продукции возрастет на 0,2%.

Общий вывод: Сравнивая коэффициенты эластичности можно сделать вывод, что фактор х₁ оказывает наибольшее влияние на зависимую переменную (у), поскольку > .

5) Оценка статистической значимости коэффициентов регрессии. С этой целью используем критерий Стьюдента.

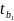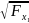= = 4,45;

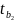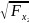= = 1,39.

Табличное значение данного критерия при уровне значимости α=0,05 и степени свободы k=n-m-1=17 составит 2,11.

Вывод: Анализируя полученные расчетные значения с табличным, можно сделать вывод, что признается статистическая надежность параметра b₁, т.к. > t_табл , статистическая значимость параметра b₂ не подтверждается, т.к. <t_табл .

6) Расчет прогнозных уровней.

Точечный прогноз получают путем подстановки прогнозных уровней в уравнение регрессии. При х₁=7 и х₂=26 рассчитываем уравнение.

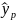= 1,835 + 0,946 ∙ 7 + 0,0856 ∙ 26 = 10,6826 тыс.руб.

Интервальный прогноз:

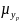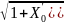= S∙ , где

– ошибка прогнозного значения;

S – стандартная ошибка.

S = 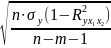= = 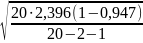0,15

- ( 1 7 26 )

X₀ -

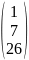
(X^’ ∙ X)^-1 = ∙ ,

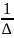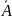где – присоединенная матрица

X^’X =

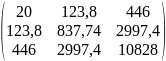
∆ = 139940,08

=

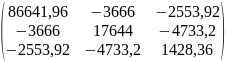
(X^’X)^-1 =

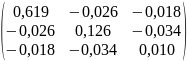
(X^’∙ X)^-1X₀ = 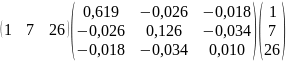=0,0697

= 0,15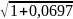 = 0,1551

, где

t_T - табличное значение критерия Стьюдента (2,11).

=

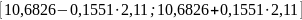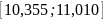
Вывод: Прогнозное значение выработки продукции при условии, что значение переменных достигнут уровней x_1p = 7, x_2p = 26, составит 10,6826 тыс.руб. и будет варьировать в интервале .

Список использованной литературы

1. Кремер Н.Ш., Путко Б.А. Эконометрика. - 3-е изд., перераб. и доп. -М.: Юнити-Дана, 2010. — 328 с. 

2. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. — М.: Дело, 2007. — 504 с.

3. Эконометрика. Учебник / Под ред. Елисеевой И.И. — 2-е изд. — М.: Финансы и статистика, 2006. — 576 с.