Критерий Фишера. Проверка адекватности эмпирических моделей.

Для практического использования моделей регрессии большое значение имеет их адекватность, т. е. соответствие фактическим статистическим данным.

Адекватность регрессионной модели при малой выборе можно оценить F критерием Фишера:

,

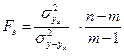где m – число параметров модели;

n - число единиц наблюдения;

- факторная дисперсия, которая характеризует вариацию результативного признака под влиянием признака фактора, включенного в модель;

- остаточная дисперсия, характеризующая вариацию результативного признака под влиянием прочих, неучтенных факторов;

- общая дисперсия, показывающая вариацию результативного признака под влиянием всех факторов, вызывающих эту вариацию:

 

.

 

Эмпирическое значение критерия сравнивается с критическим (табличным) с уровнем значимости 0,01 или 0,05 и числом степеней свободы (m-1), (n-m).

Если > , то уравнение регрессии признается значимым.

Проведем оценку адекватности регрессионной модели , выражающей зависимость среднего объема привлеченных средств банков от собственных средств, с помощью F критерия Фишера:

 

;

;

 

;

 

.

 

Табличное значение F_т с уровнем значимости 0,05 и числом степеней свободы (2-1), (15-2) равно 4,68. (См. Приложение 7). Так как > , то уравнение регрессии можно признать адекватным.

При численности объектов анализа до 30 единиц (при малой выборе) возникает необходимость испытания параметров уравнения на их типичность (значимость). При этом осуществляется проверка, насколько вычисленные параметры характерны для отображаемого комплекса условий, не являются ли полученные значения параметров результатами действия случайных причин.

 

Гипотеза о статистической значимости всего уравнения регрессии в целом

 

Используется критерий Фишера- Снедекора F и проверяется нуль-гипотеза:

                                                                

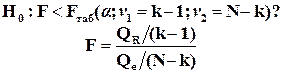
QR – сумма квадратов отклонений расчетных значений  от среднего , обусловленная вариацией факторов; Qe  - сумма квадратов отклонений расчетных значений  от фактически наблюдаемых, обусловленная влиянием случайных возмущений Ei (включая влияние неучтенных в модели факторов).

 

                 

Выводы:

1. Если гипотеза Н0 выполнена, то уравнение регрессии в целом статистически незначимо и можно сразу делать вывод о неадекватности модели.

2. Если нуль-гипотеза Н0 не выполнена, т.е. F>Fтаб, то уравнение регрессии в целом значимо и можно переходить к проверке других гипотез.