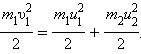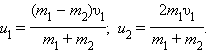Упругие и неупругие соударения

Закон сохранения механической энергии и закон сохранения импульса позволяют находить решения механических задач в тех случаях, когда действующие силы неизвестны. Примером такого рода задач является ударное взаимодействие тел.

С ударным взаимодействием тел нередко приходится иметь дело в обыденной жизни, в технике и в физике (особенно в физике атома и элементарных частиц).

Ударом (или столкновением) принято называть кратковременное взаимодействие тел, в результате которого их скорости испытывают значительные изменения. Во время столкновения тел между ними действуют кратковременные ударные силы, величина которых, как правило, неизвестна. Поэтому нельзя рассматривать ударное взаимодействие непосредственно с помощью законов Ньютона. Применение законов сохранения энергии и импульса во многих случаях позволяет исключить из рассмотрения сам процесс столкновения и получить связь между скоростями тел до и после столкновения, минуя все промежуточные значения этих величин.

В механике часто используются две модели ударного взаимодействия – абсолютно упругий и абсолютно неупругий удары.

Абсолютно неупругим ударом называют такое ударное взаимодействие, при котором тела соединяются (слипаются) друг с другом и движутся дальше как одно тело.

При абсолютно неупругом ударе механическая энергия не сохраняется. Она частично или полностью переходит во внутреннюю энергию тел (нагревание).

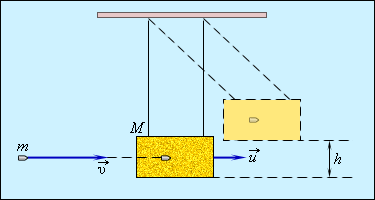
Примером абсолютно неупругого удара может служить попадание пули (или снаряда) в баллистический маятник. Маятник представляет собой ящик с песком массой M, подвешенный на веревках (рис. 1.21.1). Пуля массой m, летящая горизонтально со скоростью   попадает в ящик и застревает в нем. По отклонению маятника можно определить скорость пули.

Обозначим скорость ящика с застрявшей в нем пулей через   Тогда по закону сохранения импульса 

При застревании пули в песке произошла потеря механической энергии: 

Отношение M / (M + m) – доля кинетической энергии пули, перешедшая во внутреннюю энергию системы: 

Эта формула применима не только к баллистическому маятнику, но и к любому неупругому соударению двух тел с разными массами.

При m << M   почти вся кинетическая энергия пули переходит во внутреннюю энергию. При m = M 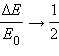  – во внутреннюю энергию переходит половина первоначальной кинетической энергии. Наконец, при неупругом соударении движущегося тела большой массы с неподвижным телом малой массы (m >> М) отношение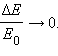 

Дальнейшее движение маятника можно рассчитать с помощью закона сохранения механической энергии: 

где h – максимальная высота подъема маятника. Из этих соотношений следует: 

Измеряя на опыте высоту h подъема маятника, можно определить скорость пули υ.

Рисунок 1.21.1. Баллистический маятник

Абсолютно упругим ударом называется столкновение, при котором сохраняется механическая энергия системы тел.

Во многих случаях столкновения атомов, молекул и элементарных частиц подчиняются законам абсолютно упругого удара.

При абсолютно упругом ударе наряду с законом сохранения импульса выполняется закон сохранения механической энергии.

Простым примером абсолютно упругого столкновения может быть центральный удар двух бильярдных шаров, один из которых до столкновения находился в состоянии покоя (рис. 1.21.2).

Центральным ударом шаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.

Рисунок 1.21.2. Абсолютно упругий центральный удар шаров

В общем случае массы m₁ и m₂ соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии 

Здесь υ₁ – скорость первого шара до столкновения, скорость второго шара υ₂ = 0, u₁ и u₂ – скорости шаров после столкновения. Закон сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, записывается в виде: 

m1υ1 = m1u1 + m2u2.

Мы получили систему из двух уравнений. Эту систему можно решить и найти неизвестные скорости u₁ и u₂ шаров после столкновения: 

В частном случае, когда оба шара имеют одинаковые массы (m₁ = m₂), первый шар после соударения останавливается (u₁ = 0), а второй движется со скоростью u₂ = υ₁, т. е. шары обмениваются скоростями (и, следовательно, импульсами).

Если бы до соударения второй шар также имел ненулевую скорость (υ₂ ≠ 0), то эту задачу можно было бы легко свести к предыдущей с помощью перехода в новую систему отсчета, которая движется равномерно и прямолинейно со скоростью υ₂ относительно «неподвижной» системы. В этой системе второй шар до соударения покоится, а первый по закону сложения скоростей имеет скорость υ₁' = υ₁ – υ₂. Определив по приведенным выше формулам скорости u₁ и u₂ шаров после соударения в новой системе, нужно сделать обратный переход к «неподвижной» системе.

Таким образом, пользуясь законами сохранения механической энергии и импульса, можно определить скорости шаров после столкновения, если известны их скорости до столкновения.

Центральный (лобовой) удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.

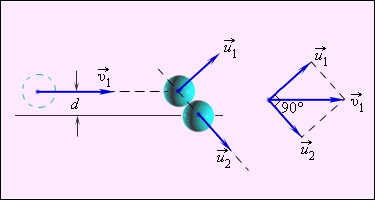
Частным случаем нецентрального упругого удара может служить соударение двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров (рис. 1.21.3).

Рисунок 1.21.3. Нецентральное упругое соударение шаров одинаковой массы. d – прицельное расстояние

После нецентрального соударения шары разлетаются под некоторым углом друг к другу. Для определения скоростей   и   после удара нужно знать положение линии центров в момент удара или прицельное расстояние d (рис. 1.21.3), т. е. расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скорости   налетающего шара. Если массы шаров одинаковы, то векторы скоростей   и   шаров после упругого соударения всегда направлены перпендикулярно друг к другу. Это легко показать, применяя законы сохранения импульса и энергии. При m₁ = m₂ = m эти законы принимают вид: 

Первое из этих равенств означает, что векторы скоростей  ,   и   образуют треугольник (диаграмма импульсов), а второе – что для этого треугольника справедлива теорема Пифагора, т. е. он прямоугольный. Угол между катетами   и   равен 90°.

Определение коэффициента восстановления,

времени соударения и силы удара взаимодействующих тел

Во многих случаях взаимодействия тел мы сталкиваемся с этой разновидностью – ударом. В частности, в строительстве – это работы по забивке свай, применение пневмомолотков и т. д. Поэтому весьма важно изучение физической стороны удара и процессов, происходящих при этом в телах.

Удар – это совокупность явлений возникающих при кратковременном приложении к телу внешних сил и связанных с изменением его скорости. При этом мерой взаимодействия тел служит изменение импульса (количества движения) тела, связанного с импульсом тела:

.

Рассеяние механической энергии при ударе характеризуется коэффициентом восстановления скорости (k_c) или коэффициентом восстановления энергии (k_э).

Коэффициент восстановления скорости определяется по формуле:

, (1)

где υ_1n и υ_2n – проекции на линию удара скоростей первого и второго тел до удара (рис. 1);

U_1n и U_2n – проекции тех же тел после удара.

При центральном ударе линия удара совпадает с линией О₁О₂, соединяющей центры масс тел и тогда υ_1n = υ₁: U_1n = U₁ и т.д. Следовательно выражение (1) переписывается в виде

, (2)

Если υ₁=0 и U₁=0, то есть первое тело массивное и неподвижное, как это осуществлено в этой работе, то

. (3)

Коэффициент восстановления энергии зависит от системы отсчёта и определяется как отношение суммарной кинетической энергии тел после удара (Е''_к) к суммарной кинетической энергии тел до удара (Е'_к).

. (4)

Величины коэффициентов восстановления зависят от физических свойств материалов соударяющихся тел, их формы, массы.

Для абсолютно неупругого удара k_э=0, а для абсолютно упругого k_э=1, для реальных случаев 0<k_э<1.

В представленной работе коэффициенты считаются зависящими только от материала соударяющихся тел. В качестве их используется шар, подвешенный на проволоках и массивный стальной куб, на котором закрепляются пластины из различных металлов (медь, алюминий свинец и бронза).

Для отклонённого на угол α₀ шара (поднятого над начальным положением на высоту h₀) можно записать, что

, или  , (5)

где h₀ – высота подъема шара над начальным положением.

Так как

, (6)

Тогда можно записать, что до удара

. (7)

После удара шара о неподвижный куб, шар отскочит на угол α₁, и можно получить аналогичное энергетическое уравнение после удара:

. (8)

Теперь можно по формулам (3) и (4) найти коэффициент восстановления. Уменьшение угла отклонения после первого удара может быть небольшим, если соударение близко к упругому и погрешность результата при этом резко возрастает. Для её уменьшения целесообразно измерять величину угла после n отскоков шара от куба. Тогда можно записать систему уравнений, дополнительных к (7) и (8):

;  ; … (9)

Коэффициент восстановления энергии для первого удара  для второго удара и т.д. Перемножим эти равенства:

;  . (10)

Аналогично соотношения можно записать для коэффициента восстановления скорости:

(11)

или

. (12)

Время соударения тел также зависит от многих факторов: относительной скорости тел, их размеров, упругих свойств материалов и т.д. В случае соударения металлических тел оно может быть измерено электрическим методом. Для этого используем схему, приведённую на рис. 2.

Зная время соударения, можно рассчитать среднюю силу удара за промежуток действия:

;  .

Так как

,

то

, (14)

где l – длина полвеса (по перпендикуляру от точки подвеса до центра шара).