1. Фильтр нижних частот (фнч) имеет три частотных полосы:

Полосу пропускания (ПП),

Полосу задержки (ПЗ) или ослабления,

Переходную полосу.

На рисунке 2.3 показана идеальная АЧХ и требования к АЧХ фильтра нижних частот.

Рисунок 2.3 Требования к АЧХ ЦФ НЧ

Полоса пропускания ограничивается частотой среза , ширина полосы пропускания ,

- максимально допустимое отклонение от ,

- максимально допустимое ослабление в полосе пропускания .

Важным обстоятельством является то, что в соответствии с методом синтеза КИХ-фильтров отклонение АЧХ от 1 (соответственно от нуля) задается симметрично 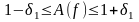, а для БИХ-фильтров отклонение задается только в одну сторону так, что АЧХ не превышала единицы и характеристика ослабления, не превышала нуля 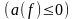, что отображено на рисунке. Это означает, что для БИХ-фильтра, синтезируемого с теми же допусками, что и КИХ-фильтр, необходимо задавать в полосе пропускания допустимое отклонение АЧХ

В абсолютных единицах или , если требования задаются к характеристике ослабления в .

Полоса задерживания или ослабления ПЗ лежит в пределах от граничной частоты до половины частоты дискретизации , ее ширина ,

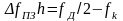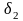- максимально допустимое отклонение АЧХ от ,

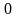- максимальное допустимое ослабление в полосе задерживания

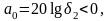
а в терминах характеристики затухания минимально допустимое затухание в полосе задерживания

Переходная полоса располагается между полосами пропускания и задерживания, ее ширина , поскольку в этой полосе требования не задаются, удовлетворительным окажется любой решение, если оно соответствует требованиям в полосах пропускания и задерживания.

Фильтр верхних частот имеет, три полосы, которые расположены в обратном порядке, относительно ФНЧ.

Цифровые фильтры с бесконечной импульсной характеристикой (БИХ)

БИХ фильтры имеют традиционные аналоговые эквиваленты (фильтр Баттерворта, Чебышева, эллиптический и Бесселя) и могут быть проанализированы и синтезированы с использованием традиционных методов проектирования фильтров. БИХ фильтры получили такое название, потому что их импульсные характеристики растянуты на бесконечном временном интервале. Это объясняется тем, что данные фильтры являются рекурсивными, т.е. используют обратную связь.

Характеристики БИХ- фильтров:

1. импульсная характеристика имеет бесконечную длительность.

2. фазовая характеристика нелинейная;

3. более эффективны;

4. устойчивость гарантирована не всегда, необходимо проверка на устойчивость;

5. имеют аналоговые прототипы;

6. рекуррентны;

7. экономнее с точки зрения необходимых вычислений, так и с точки зрения требований к памяти;

8. определения меньшего числа коэффициентов.

Цифровые БИХ-фильтры характеризуются следующим рекурсивным уравнением:

(2.1)

и передаточной функцией

, (2.2)

.

где и 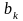- коэффициенты фильтра,

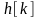- импульсная характеристика фильтра, длительность которой теоретически бесконечна,

- передаточная функция фильтра.

В уравнении (2.1) текущая выходная выборка является функцией прошедших выходов , а также текущей и прошедших входных выборок , , т.е. БИХ- фильтр это система с обратной связью. Достоинство БИХ фильтров - гибкость, которую обеспечивает обратная связь.

Разработку цифровых БИХ-фильтров можно разбить на пять этапов [14].

1. спецификация требований к фильтру,

2. расчет коэффициентов 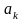и передаточной функции .

3. выбор структуры фильтра, обычно в БИХ-фильтрах используются параллельная структура или каскады блоков второго и первого порядка.

4. анализ ошибок, которые могут появиться при представлении коэффициентов фильтра и выполнении арифметических операций, фигурирующих при фильтрации, с помощью конечного числа битов.

5. реализация фильтра на программном или аппаратном уровне.

Этапы разработки фильтров показаны на рисунке 2.2.

Рисунок 2.4. Этапы разработки цифровых фильтров

Разработка БИХ-фильтров начинается с составления списка требований к производительности. В спецификациях должны указываться характеристики сигнала, частотная характеристика фильтра, способ реализации. У фильтров таких как фильтры нижних частот и полосовые фильтры, спецификация частотной характеристики часто задается в форме схемы допусков.

В данной главе водробно рассматриваются некоторые методы проектирования цифровых фильтров и использование этих методов.Основное внимание направлено на рассмотрение методов расчета в частотной области и на обработку больших потоков данных, а не на методы расчета во временной области и обработку коротких информационных сообщений. Совершенно не затрагиваются вопросы проектирования цифровых фильтров с точки зрения теории оптимальных фильтров и теории оценки сигналов при наличии шумов. Эти вопросы широко освещаются в литературе.