3.5 Средний температурный напор

Δ

(13)

При многоходовом потоке теплоносителя в трубном пространстве холодильника и одноходовом потоке теплоносителя в межтрубном пространстве средний напор по методу Белоконя [5,c.561]:

Здесь Δ средний температурный напор, К; соответственно большая и меньшая разность температур, определяемая по формулам:

ΔТ ΔТ

(14)

Где θ – разность среднеарифметических температур горячего и холодного теплоносителей.

(15)

А ΔТ – характеристическая разность температур горячего и холодного теплоносителей

ΔТ =

(16)

Рассчитаем ΔТ по формуле:

Где Δ = перепад температур в горячем потоке; Δ перепад температур в холодном потоке; Р – индекс противоточности. Р = 0,98 [10, с.562].

Находим:

Δ = 363 – 323 = 40 К;

Δ

ΔТ =

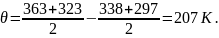
Тогда

3.6 Коэффициент теплоотдачи при поперечном обтекании воздухом пучка оребренных труб

При спиральном оребрении труб, расположенных в шахматном порядке, для определения коэффициента теплоотдачи воспользуемся формулой:

(17)

Где λ = 0,0274 Вт/(м·К) – коэффициент теплопроводности воздуха при его средней температуре [3, с.547 таблица 2.1]; плотность воздуха при его средней температуре; 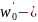скорость воздушного потока в сжатом сечении одного ряда труб оребренного пучка, м/с; динамическая вязкость воздух при средней температуре, Па·с; Pr = 0,711 –критерий Прандтля при средней температуре; – средняя толщина ребра, м.

Величину определим по формуле:

(18)

Где скорость набегающего воздушного потока при входе в трубный пучок, то есть в свободном сечении перед секциями оребренных труб; σ= ( поперечный шаг оребренных труб, принятые ранее равным 0,052 м)

σ =

высота ребра; = 0,0035 м – шаг ребер.

Скорость набегающего воздушного потока:

(19)

Где действительный секундный расход воздуха, м/с; – фронтальное к потоку воздуха сечение аппарата.

Таким образом

= 4 м/с

Средняя толщина ребра:

(20)

Где толщина ребра в его вершине; 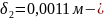толщина ребра в его основании.

Имеем:

Скорость воздушного потока в сжатом сечении:

Динамическая вязкость воздуха при средней температуре:

μ = v 17,4· Па·с [3, с.547 таблица 2.1]

Подставив в формулу значения всех величин, получим:

Вт/( )

3.7 Приведенный коэффициент теплоотдачи со стороны воздуха в случае пучка оребоенных труб

Приведенный коэффициент теплоотдачи находим по формуле [7, с 137]

(21)

Где поверхность ребер, приходящаяся на 1 м длины трубы, F_п – полная наружная поверхность 1 м оребреннойтрубы, м²/м; Е – коэффициент эффективности ребра, учитывающий понижение его температуры по мере удаления от основания, - находим по графику [53, с 52 рис 2.6]; - коэффициент, учитывающий трапецивидную форму сечения ребра, - находим по графику [7, с.52 рис2.7]; экспериментально найденный коэффициент, учитывающий неравномерность теплоотдачи по поверхности ребра; 0,0006 м²∙ К/Вт – тепловое сопротивление загрязнения наружной поверхности трубы.

Находим поверхность ребер, приходящуюся на 1 м длины трубы:

(22)

где х = 286 – число спиральных витков ребер, приходящихся на 1 м длины трубы [6, с 108 рис.2.4]:

Определяем наружную поверхность участков гладкой трубы между ребрами, приходящуюся на 1 м длины трубы:

(23)

Где – ширина ребер у основания [6, с 108 рис.2.4].

Полная наружная поверхность 1 м оребренной трубы будет равна:

(24)

Вычисляем соотношения, необходимые для пользования:

Чтобы учесть наружное загрязнение труб, необходимо вычислить подкоренные выражения аргументов графических зависимостей [7, с 52 рис 2.6 и 2.7] и поделить их на величину (1+β₃ψα_к):

=

(25)

=

Здесь = 201,2 Вт / (м∙К) – коэффициент теплопроводности алюминиевого ребра трубы.

Так как , то

Тогда по графику [53, с 52 рис 2.6]Е = 0,98 , [7, с 52 рис 2.7] .

Определяем приведенный коэффициент теплоотдачи: