лаб_1 - Исследование свойств типовых линейных звеньев / лаб_1_отчет

МИНИСТЕРСТВО ВЫСШЕГО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ОБРАЗОВАНИЯ

«МАГНИТОГОРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Г.И. НОСОВА»

Кафедра автоматизированного электропривода и мехатроники

Лабораторная работа № 1

Исследование свойств типовых линейных звеньев

систем автоматического регулирования

Вариант – 2

Выполнил:

Проверил:

Магнитогорск, 2020

Цель работы: В данной работе должны быть получены кривые переходных процессов на выходах U_ВЫХ(t) следующих звеньев:

а) интегрирующего с передаточной функцией W1(p) = ;

б) инерционного или апериодического 1^го с передаточной функцией W2(p);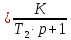

в) пропорциональноинтегрирующего с передаточной функцией W3(p);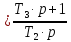

г) реально дифференцирующего с передаточной функцией W4(p)

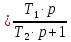
Для каждого исследуемого звена необходимо получить зависимости U_ВХ(t) и U_ВЫХ(t) для двух видов входных воздействий. Также необходимо получить частотные характеристики (ЛАЧХ и ЛФЧХ) каждого звена, отметить на них частоты среза и сопряжения, если таковые имеются.

В отчёте по лабораторной работе по результатам моделирования установить, как зависят величина и характер изменения U_ВЫХ(t) от:

1. характера изменения входного сигнала U_ВХ(t) (величины скачка, установившегося значения, темпов нарастания, спадания);

2. параметров исследуемого звена (К_i, Т_i).

Таблица 1.1 – Параметры звеньев.

№ вар.	1	2	3	4	5	6	7	8	9	10	11	12
К	2	3	6	7	9	11	13	15	17	19	20	22
Т1	1	1.5	1.7	2.0	2.5	3.0	4.5	5.0	6.0	7.0	8.0	9.0
Т2	0.1	0.2	0.3	0.5	0.7	0.9	1.1	0.8	0.6	0.4	0.2	0.3
Т3	0.3	0.5	0.7	0.9	1.1	1.3	0.8	0.6	0.4	0.2	0.35	0.45

Таблица 1.2 – Параметры входных сигналов по вариантам.

№ вар.	1	2	3	4	5	6	7	8	9	10	11	12
U0	5	7	9	13	15	14	12	10	8	6	4	2
t1	2	2	2	2	2	2	2	2	2	2	2	2
t2	7	11	15	9	13	10	8	12	7	16	17	19
t3	10	15	20	11	17	13	14	15	11	19	20	17
t4	12	18	23	14	19	17	16	19	13	24	23	20

Интегрирующее звено

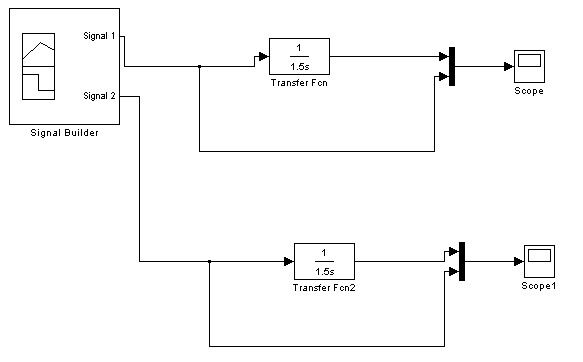
Рисунок 1 - Схема с интегрирующим звеном.

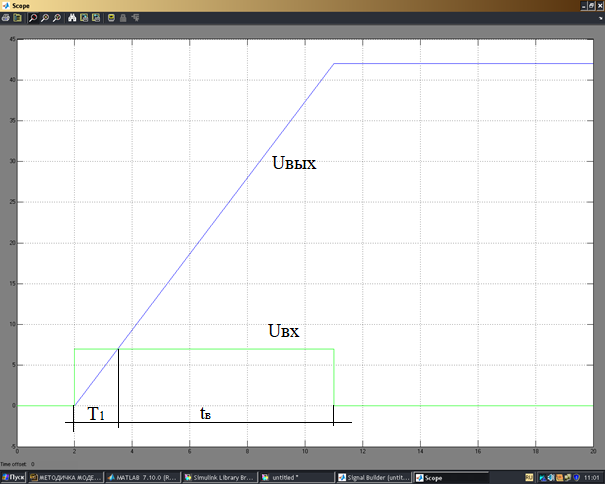
Рисунок 2 – График переходного процесса при скачкообразном воздействии.

Рисунок 3 – График переходного процесса при линейном воздействии.

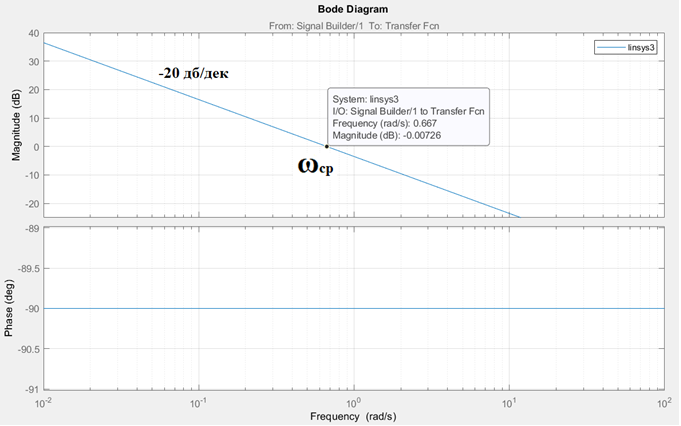
Рисунок 4 - Частотная характеристика.

Инерционное или апериодическое звено 1^го порядка

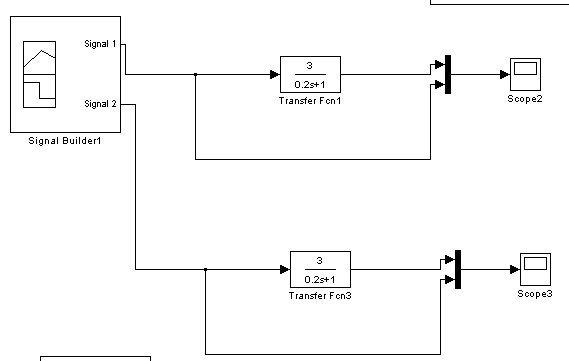
Рисунок 5 – Схема с инерционным звеном.

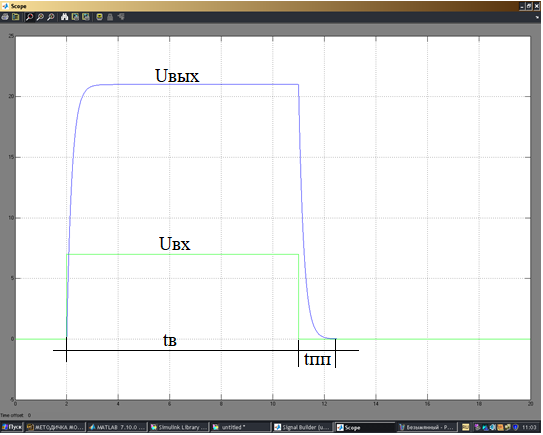
Рисунок 6 - График переходного процесса при скачкообразном воздействии.

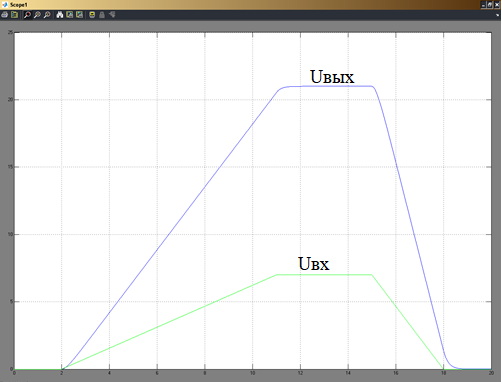
Рисунок 7 - График переходного процесса при линейном воздействии.

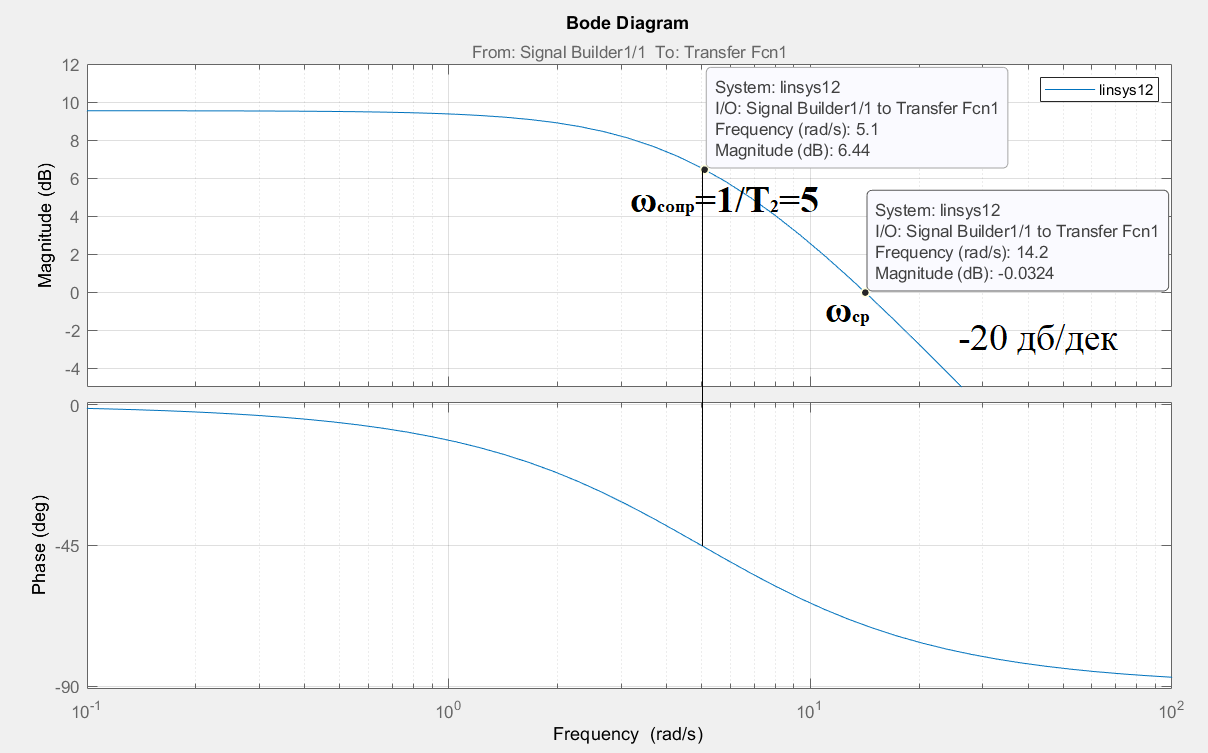
Рисунок 8 - Частотная характеристика.

Пропорционально-интегрирующее звено

Рисунок 9 – Схема с пропорциональноинтегрирующим звеном.

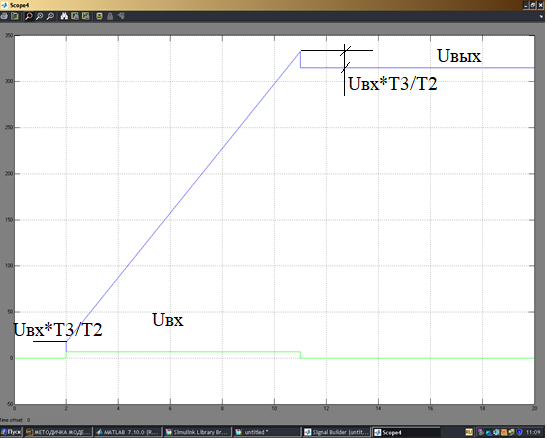
Рисунок 10 - График переходного процесса при скачкообразном воздействии.

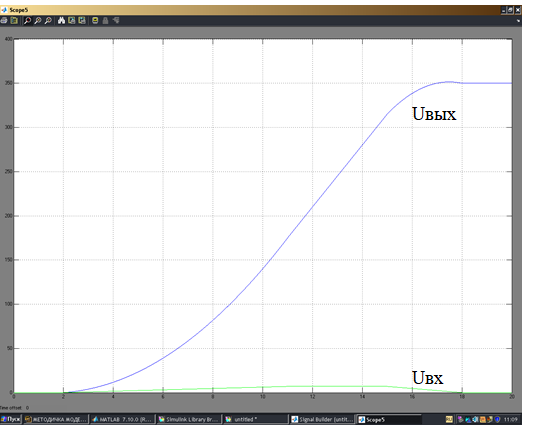
Рисунок 11 - График переходного процесса при линейном воздействии.

Рисунок 12 - Частотная характеристика.

Реально дифференцирующее звено

Рисунок 13 – Схема с реально дифференцирующим звеном.

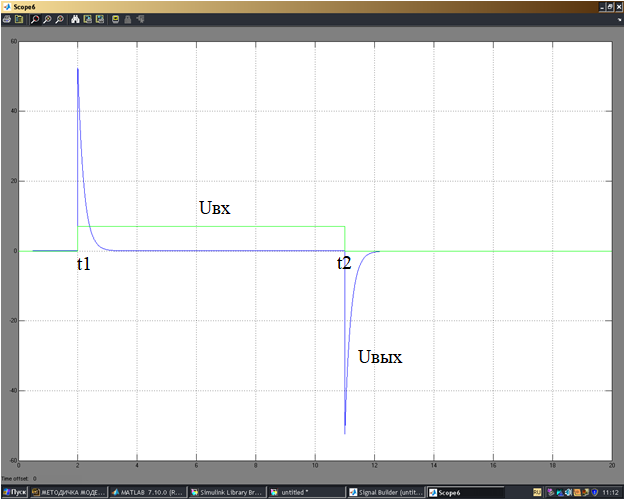
Рисунок 14 - График переходного процесса при скачкообразном воздействии.

Рисунок 15 - График переходного процесса при линейном воздействии.

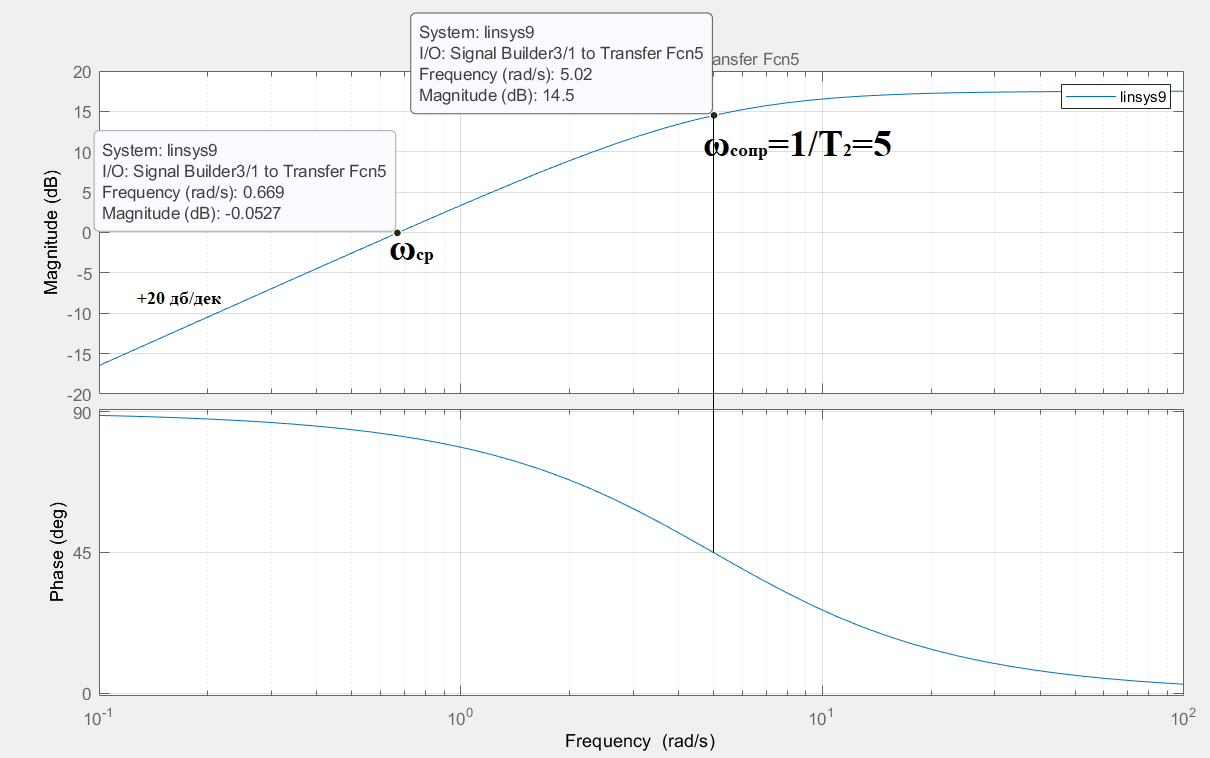
Рисунок 16 – Частотная характеристика.

Вывод: По результатам моделирования можно установить, как зависят величина и характер изменения U_ВЫХ(t):

1. Интегрирующее звено:

   1. При постоянном (скачкообразном) значении входного напряжения, выходное изменяется по линейному закону :

.

При снятии входного напряжения, выходное остается на том же уровне (свойство интегратора).

2. При линейном воздействии входного сигнала в промежуток времени t₁-t₂ входной сигнал изменяется по линейной зависимости, т.е. U_ВХ=tk.

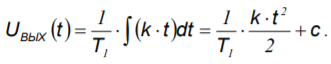
В промежуток времени t₂-t₃ входной сигнал не изменяется, выходное напряжение имеет линейный характер. В промежуток времени t₃-t₄ выходное напряжение линейно уменьшается U_ВХ=-kt. В момент времени t4 входной сигнал равен нулю, интегратор перестает интегрировать входное напряжение.

2. Инерционное звено:

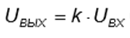
   1. При скачкообразном входном воздействии

Переходная функция апериодического звена имеет вид и во время переходного процесса выходной сигнал имеет экспоненциальный характер.

2. При линейном воздействии входного сигнала

В промежутки времени t₁-t₂ и t₃-t₄ выходной сигнал отстает от входного по времени за счет инерции звена. С момента времени t₂ выходной сигнал по экспоненциальной зависимости стремится к входному.

3. Пропорционально-интегрирующее звено (ПИ-звено):

   1. При скачкообразном входном воздействии, с момента времени t₁ выходной сигнал скачком увеличивается пропорционально величине , с последующим интегрированием входного напряжения. В момент времени t₂ входной сигнал скачком уменьшается до нуля, выходной сигнал, в свою очередь, также пропорционально уменьшается на величину . С момента времени t₂ , за счет свойств интегратора, выходное напряжение не изменяется.

   2. При линейном воздействии входного сигнала в промежутки времени t₁-t₂ и t₃-t₄ выходной сигнал представляет собой квадратичную зависимость (параболу), сложенную с пропорциональной составляющую ПИ-звена

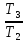
4. Реально-дифференцирующее звено:

   1. При скачкообразном воздействии в момент времени t₁ происходит дифференцирование скачкообразно изменяющегося входного напряжения, а затем экспоненциальный спад выходного напряжения до нуля, вызванный постоянным (неизменным) напряжением U_вх , U_вх  0 . Затем, с момента времени t₂ входное напряжение скачком снимается,

   2. При линейно изменяющемся входном сигнале Входное напряжение на промежутке времени t₁-t₂ линейно нарастает, т.е. его можно представить, как U_ВХ=tk, где

Продифференцировав эту зависимость, получим:

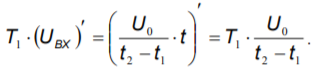
U_вх на промежутке t₂-t₃постоянно, поэтому его производная равна нулю. На промежутке t₃-t₄ производная входного сигнала отрицательная.