1. Линейные пространства. Размерность и базис.

Определение: n – мерным вектором называется упорядоченнаяn-ка чисел, x = (x₁, x₂, … , x_n), x_i Є R, i = 1,. . . , n. Числа x₁, x₂, … , x_n – координаты вектора, или компоненты вектора х. Часто n – мерные векторы удобно рассматривать как матрицу-строку, или матрицу столбец. Суммой векторов x = (x₁, x₂, … , x_n) и у = (у₁, у₂, … , у_n) называется вектор x + у = (x₁ + у₁, x₂ + у₂, … , x_n + у_n). Произведением x = (x₁, x₂, … , x_n) на α Є R вектор αx = (αx₁, αx₂, … , αx_n). Нулевой вектор 0=(0,0,…,0).

Определение: Непустое множество n – мерных векторов для которых определены операции сложения и умножения на число назовем векторным, или линейным пространством над числовым полем R чисел, если выполняются следующие аксиомы:

1. сложение векторов ассоциативно x, y ,z Є Rⁿ (x + y) + z = x + (y + z)

2. сложение векторов коммутативно x, y Є Rⁿx + y = y + x

3. существует нулевой вектор 0: x Є Rⁿ0 + х= х + 0.

4. существует противоположный вектор x Є Rⁿ -х: x + (-x) = -x + x =0.

5. умножение вектора на число ассоциативно x Є Rⁿ α, β Є R: α (βx) = (αβ)x

6. 1Є R: x Є Rⁿ: 1 ^.x = x^. 1= x

7. дистрибутивность операции умножения вектора на число относительно сложения векторов α Є R

x, у Є Rⁿα (x + y) = αx + αy

8. дистрибутивность операции умножения вектора на число относительно суммы чисел α, β Є R, x Є Rⁿ

(α + β)x = αx +βx

Пример: 1. Rⁿ – арифметическое векторное пространство. 2. Пр-во матриц раз-ти m*n 3. M_n– многочленов степени не выше n. 4. Пр-во линейных операторов.

Определение: Линейной комбинацией векторов x₁, x₂, … , x_k Є Rⁿи чисел α₁, α₂, . . ., α_k называется вектор x = α₁x₁+ α₂x₂ + … + α_kx_k, x = .

Определение: Рангом системы векторов называется максимальное число линейно независимых векторов системы.

Определение: Множество V всех линейных комб-ций векторов x₁, x₂, … ,x_k называется линейной оболочкой порожденной этими векторами

<x₁, x₂, … ,x_k> = V

Примеры: плоскость - линейная оболочка пары неколлинеарных векторов; мн-во всех векторов, парал-ых ОХ это лин-ая обол-ка, порожденная, напр., вектором (5, 0,…,0).

Определение: Система векторов x₁, x₂, … ,x_kназывается линейно зависимой, если существует нетривиальная линейная комбинация векторов этой системы, равная нулевому вектору. Если только тривиальная комбинация векторов любой системы равна нулю, то эта система называется линейно-независимой.

Определение: Линейно независимая упорядоченная система векторов x₁, x₂, … , x_r Є V называется базисом, если любой вектор х представим в виде:

х=х1*а1+х2*а2+…+хn*an

где х1, х2, …, хn координаты вектора х в этом базисе.

Пример:<i, j> =R² базис R² , <i, j, k>=R³ базис R³.

Теорема: В пространстве Rⁿсуществует по крайней мере один базис.

Лемма: Пусть V линейная оболочка в Rⁿc базисом В = {е_1, е₂,…, е_r}. Пусть

{ y_1,y₂,…, y_s }- линейно-независимая система векторов из V, тогда s ≤r.

Теорема о базисе линейной оболочки!!!: 1. Каждая ненулевая линейная оболочка обладает конечным базисом. 2. Все базисы оболочки V состоят из одинакового числа векторов, это число обозначим r, причем r≤n, и назовем его размерностью данной линейной оболочки dimV = r.

Док-во: 1. По условию V≠0 => содержит хотя бы один ненулевой вектор х₁. Если в V не сущ-ет векторов лин. нез-ых с х₁, то процесс окончен, если сущ-ет, то: пусть мы нашли в V линейно-независимую систему векторов х₁, х₂ , … , х_k, где k≥1. Если линейная оболочка < х₁, х₂ , … , х_k>=V, то эти векторы образуют базис этой линейной оболочки. Если же эта линейная оболочка ≠V, то тогда существует вектор х_k+1 не являющийся линейной комбинацией х₁, х₂ , … , х_k, тогда система векторов х₁, х₂ , … , х_k, х_k+1 – линейно нез-ма. Рассуждая аналогично, мы можем продолжить неограниченно процесс расширения линейно-независимой системы, но все векторы х_iЄ V,

=> х_iЄ Rⁿ , но в Rⁿ векторы { е_1, е₂,…, е_n } образуют базис, а по лемме линейно-независимая система в пространстве Rⁿ содержит n векторов. Значит, при некоторомr≤n процесс закончится. Т.е. r≤n , r N :<х₁, х₂ , … , х_k,…, х_r>=V => векторы х₁, х₂ , … , х_k,…, х_rобразуют базис линейной оболочки V.

2. Предположим, что {y₁,y₂,…,y_s }– тоже базис линейной оболочки, тогда по лемме s≤r, но и r≤s одновременно (меняем местами лин. независ. сис-му и базис), т.е. r=s. Ч.т.д.

Итак, с каждой линейной оболочкой V пространства Rⁿ ассоциируется целое положительное число r≤n, которое назвали размерностью этой оболочки. Из доказательства предыдущей теоремы следует, что размерность линейной оболочки можно определить, как максимальное число линейно-независимых векторов этой оболочки, dimRⁿ = n.

Пример: 1. Rⁿ – арифметическое векторное пространство dimRⁿ = n. 2. Пр-во матриц раз-ти m*ndimM_m*n = m*n.

3. M_n– многочленов степени не выше n

dimM_n= n+1.

Теорема: Для того, чтобы сложить вектора, надо сложить их координаты в одном базисе, а при умножении вектора на число координаты умножаются на это число.

Определение: Множество К векторов из линейного пространства L называется линейным подпространством, если сумма х+у любых двух векторов х и у из L принадлежит, и произведение а*х любого числа а и вектора х из L принадлежит К.

Линейное пространство есть линейная оболочка векторов своего базиса.

2. Евклидовы пространства. Построение ортонормированного базиса.

Определение: Пусть V действительное линейное пространство. Отображение V^*V→ P называется скалярным произведением, если оно удовлетворяет следующим аксиомам: , , Є V, α Є P

1. ( , ) = ;

2. (α , ) = α ( , );

3. ( + , ) = ( , )+( , );

4. ( , ) ≥ 0, ( , ) = 0, тогда и только тогда, когда – нулевой вектор.

Определение: Вещественное линейное пространство называется евклидовым (Е), если каждой паре элементов x и y, этого пространства поставлено в соответствие действителньное число, называемое скалярным произведением.

Пример: 1) в Rⁿ, ( , ) =

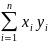
2) в пр-ве С[0;1]- ф-ций непр-ых на [0:1], роль скал-го произ-я играет отображ-е (f; g) =

Свойства скалярного произведения.

Следуют из аксиом.

1. ( , + ) = ( )= = =( , )+( , );

2. ( , α ) = = = = ( , );

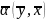3. ( , )=0 Є Е – нулевой вектор;

4. ( , 0) = (0, )=0.

Любое подпространство пр-ва Е является евклидовым пространством.

Теорема1: Для любых , Є Е имеет место неравенство: ( , )² ≤ ( , ) ^. ( , ) (1) – неравенство Коши-Буняковского;

(Примечание: х,у,е – писать со знаком в-ра.)

В матричной форме:

(2)

Теорема 2: Неравенство Коши-Буняковского обращается в равенство , когда векторы х и у коллинеарные.

Определение: В евклидовом пространстве длиной вектора х называют значение арифметического квадратного корня из скалярного квадрата вектора .

Свойства:

1) x из Е имеет длину |х| , |х| ≥0‌ , ‌ х ‌ ≠0, ‌ |х| ‌ =0 х – нулевой вектор;

2)

3) Неравенство Коши-Буняковского может иметь вид: ‌ |(х, у)| ‌ ≤ ‌| х| ‌| у| ‌ (3)

Определение: Вектор единичной длины называется нормированным. Любой ненулевой вектор можно нормировать, разделив его на число, обратное его длине.

Теорема 3: В евклидовом пространстве для любых х, у имеют места неравенства: | |‌ х|‌- |у| | ‌ ‌ ≤ |х+у| ‌ ≤|х| ‌+‌|у| ‌ (4) -неравенство треугольника.

Определение: В евклидовом пространстве углом между ненулевыми векторами называют угол 0 ≤ φ<π ,для которого

(5)

Определение: Два вектора x и у называются ортогональными, если (х, у) =0. Из этого определения следует, что нулевой и только нулевой вектор ортогонален любому вектору пространства. В евклидовом пространстве ортогональность векторов х и у означает, что либо один из них нулевой, либо угол между ними 90⁰.

Определение: Система векторов x₁, x₂, … ,x_k Є E (U) называется ортогональной, если все векторы попарно ортогональны, т.е. (x_i, x_j)=0. при i≠j.

Определение: Система векторов x₁, x₂, … , x_k называется ортонормированной, если (x_i, x_j)=δ_ij, где δ_ij – символ Кронекера δ=1, при i=j, δ=0, при i≠j.

Теорема 4!!!: Ортогональная система ненулевых векторов линейно-независима.

Док-во: Составляем линейные комбинации α_i (x_i, x_i)=0, (x_i, x_i) ≠0, след-но, α_i=0, i=1,…,k. Система векторов линейно-независима.

Следствие1: Ортонормированная система векторов линейно-независима.

Следствие2: В n-мерном евклидовом пространстве любая ортонормированная система из n векторов образует базис, такой базис называется ортонормированным. В={e₁,…, e_n}, (e_i, e_j)=δ.

Теорема 5: В евклидовом (унитарном) пространстве координаты вектора х в базисе В={e₁,…, e_n}, вычисляются по правилу: x_i = (x,e_i),i=1,…,n(6) базис В ортонормированный.

Теорема 6: В евклидовом (унитарном) пространстве скалярное произведение векторов , вычисляется по правилу (для E) (7) когда базис ортонормированный.

Теорема 7!!!: В конечномерном евклидовом пространстве существует ортонормированный базис.

Док-во: Воспользуемся индукцией по размерности пространства n. Пусть dimE = n.

1. Для n=1 теорема выполняется. aЄЕ¹, а- ненулевой вектор,

2. Пусть верно для n=k, т.е. в любом к-мерном евклидовом пространстве существует ортонормированный базис. Покажем, что он существует и в к+1-мерном евклидовом пространстве. Пусть Е^к+1

В={e₁,e₂,…,e_k+1}-некоторый базис пространства Е^к+1, L(e₁,e₂,…,e_k) является к-мерным пространством и в нем по предположению существует ортонормированный базис. В_орт={n₁,n₂,…,n_k}, т.к. вектор e_k+1 не принадлежит L(e₁,e₂,…,e_k), то вектор b_k+1= e_k+1- α₁n₁- α₂n₂- … - α_kn_k, то этот вектор ненулевой для любого α_iиз R. Выберем коэффициент α_iиз условия ортогональности вектора b_k+1 всем векторам n₁,n₂,…,n_k, т.е. (b_k+1,n_i)=0, где i=1,…,k

(b_k+1,n₁)= (e_k+1,n₁)- α₁=0, (e_k+1,n₁) - α₁=0,

(b_k+1,n₂)= (e_k+1,n₂)- α₂=0,…

Таким образом, α_i= (e_k+1,n_i), i=1,…,k. Положив , получим ортонормированный базис В={n₁,n₂,…,n_k, n_k+1 } пространства Е^к+1.

В доказательстве этой теоремы описан алгоритм последовательного построения ортонормированного базиса по данному произвольному базису.

Он называется процессом ортогонализации Грамма-Шмидта.

1. Пусть задан произвольный базис а₁,…, а_р, полагаем b₁=a₁, e₁=b₁/ | b₁‌|

k (k≥2). Положим b_k= a_k- α₁e₁- α₂e₂-…α_k-1e_k-1 , где α_i определяются из равенства:

α_i =(a_k,e_i), i=1,…,k-1 , e₁=b_k/ ‌|b_k‌|

Через р шагов получим ортонормированный базис е₁,…,е_р данного пространства.

Пример: ортогонализировать базис а₁(-2,0) и а₂(1,1).

1. b₁=a_1, e₁=b₁/‌| b₁‌| =b₁/2=(-1,0)

2. b₂=a₂-α₁e₁

α₁=(a₂,e₁) = -1+0=-1

e₂=b₂/‌ | b₂‌| = (0,1), e₂=(0,1)

b_k=a_k-α₁e₁-α₂e₂-…α_k-1e_k-1

3. Определение и свойства линейного оператора. Ядро и образ. Матрица линейного оператора.

Примечание: х,у – писать со знаком в-ра

Определение: Пусть V и W – линейные пространства над полем Р. Отображение φ: V → W называется линейным отображением пространства V в W, или линейным оператором, действующим из V в W, если x, y Є V, α Є P выполняются следующие условия:

1) φ (х+у)= φ(х)+ φ(у);

2) φ(αх)= α φ(х).

Если V и W совпадают, то φ – называют линейным оператором, действующим в V. Множество всех линейных операторов, действующих из из V в W будем обозначать (V,W). Два оператора будем называть равными, когда x Є V, φ, ψ Є (V,W)φ(x)= ψ(x).

Примеры: 1) δ :М_n → М_n-1, М_n – пространство многочленов степени ≤ n с вещественными коэффициентами., причем δ(P(t))=P (t), оператор δ – оператор дифференцирования, это линейный оператор.

2) отображение : V → W, (х) = , x Є V, Є W, – нулевой оператор.

3) – оператор проектирования.

4) – тождественный (единичный) оператор.

Из определения линейного оператора следуют его простейшие свойства:

1. Линейный оператор переводит нулевой вектор в нулевой. Док-во: пусть 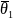Є V, Є W –нулевые вектора. Найдем образ φ( )= φ(0 ^. х) = 0^.φ(х)= _.

2. Линейный оператор переводит линейную комбинацию векторов в линейную комбинацию их образов, причем с теми же коэффициентами.

3. Линейный оператор линейно-независимую систему векторов переводит в линейно-независимую систему векторов.

Анализируя свойство 2, заметим, что для задания линейного оператора φ достаточно определить его только на векторах e₁,…e_n некоторого базиса пространства V. Тогда зная φ(e₁),…, φ(e_n) можно найти образ любого вектора из V.

Теорема 1: Пусть e₁,…e_n – базис пространства V, а g₁,…,g_n – произвольные векторы из W. Тогда существует и при том единственный линейный оператор φ Є (V,W) , переводящий векторы e₁,…e_n в g₁,…,g_nсоответственно, т.е φ(e_i)= g_i.

Следствие: Операторы φ и ψ из (V,W), равны тогда и только тогда, когда они совпадают на векторах некоторого базиса из V.

B={e₁,…,e_n} Є V, B^’ ={ e₁^’,…,e^’_m}ЄW. Из теоремы 1 следует, что линейный оператор φ однозначно определен заданием векторов φ(e₁),…,φ(e_n), а эти вектора в свою очередь в базисе В^’ однозначно определены своими координатами: φ(e₁),…,φ(e_n).

(1)

Тогда матрица (2) наз-ся матрицей оператора φ в паре базисов ВВ^’.

Из единственности разложения вектора по базису следует, что при фиксированных базисах В и В^’ матрица линейного оператора определена однозначно.

Теорема 2: Пусть dimV = n, dimW = m, тогда существует взаимнооднозначное соответствие между линейными операторами из

L (V,W) и матрицами из P^mxn , элементами кот-го являются числа из поля Р.

Теорема 3: Пусть φ Є (V,W). Если у= φ(x), то координаты у в В^’

(3)

Теорема 4: Матрицы А_{В1’ В1} и А_{В2’ В2} линейного оператора в различных парах базисов связаны следующим соотношением: А_{В2’ В2}= D^-1 А_{В1’ В1}C (4)

Определение: Две матрицы А и В называются эквивалентными, если существует невырожденные матрицы Q и Z : B=Q^.A^.Z, имеют одинаковый ранг.

Следствие из теоремы 4:

1. Матрицы линейного оператора в различных парах базиса эквивалентны.

2. Ранг матрицы линейного оператора не зависит от выбора пары базисов.

3. Две матрицы А и В размерности mxn эквивалентны тогда и только тогда, когда они являются матрицами одного и того же линейного оператора , dimv = n, dimW = m.

Определение: Образом линейного оператора наз-ся множество всех образов векторов из V при действии на них оператором φ: .

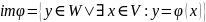Определение: Ядром линейного оператора наз-ся множество всех векторов из V, которые оператор φ переводит в нулевой вектор. , -нулевой в-р.

Примеры: 1) δ :М_n → М_n (в пространстве многочленов M_n), δ – оператор дифференцирования. im δ = M_n-1, ker δ = M₀.

2) , – тождественный оператор, im = V, ker = .

3) – нулевой оператор, im = , ker =V.

4) – оператор проектирования, .

Теорема 5!!!: Если , то пространство im φ – линейное подпространство пространства W, ker φ – линейное подпространство V.

Определение: Рангом линейного оператора называется размерность его образа.

Определение: Дефектом линейного оператора называется размерность его ядра.

rang φ = dim im φ, def φ = dim ker φ

Теорема 6:Длялюбого лин-го оп-ра : im φ=<φ(e₁), …, φ(e_n)>, где B={ e₁,…e_n }- базис пр-ва V.

Теорема о ранге и дефекте!!!: rang φ + def φ = dimV

Д-во: Пусть { e₁,…e_k }- базис ядра оп-ра φ. Дополним этот базис векторов до базиса пр-ва V векторами e_k+1,…e_n. По теореме 6 im φ=< φ(e₁), …, φ(e_k), φ(e_k+1), …, φ(e_n)> = < φ(e_k+1), …, φ(e_n)>. Д-ем, что φ(e_k+1), …, φ(e_n) лин-но нез-мы. Пред-м прот-е они лин-но зав-мы => нетрив-ая лин-ая комб-я равна 0.

α_k+1 φ (e_k+1)+ …+ α_n φ(e_n)=0 =>φ( α_k+1e_k+1+ …+ α_ne_n)=0 =>α_k+1e_k+1+ …+ α_ne_n kerφ но тогда этот вектор линейно выражается через базисные векторы ядра e₁,…e_к что невозможно в силу линейной независимости в-в e₁, …, e_k, e_k+1, …, e_n .=> φ(e_k+1), …, φ(e_n) лин-но нез-мы.

dim im φ=n-k=rang φ

dim ker φ=k=def φ

rang φ+def φ=n-k+k=n=dim V

4. Собственные значения и собственные векторы линейного оператора.

Примечание: х,у – писать со знаком в-ра.

Определение: Пусть V и W – линейные пространства над полем Р. Отображение φ: V → W называется линейным отображением пространства V в W, или линейным оператором, действующим из V в W, если x, y Є V, α Є P выполняются следующие условия:

1) φ (х+у)= φ(х)+ φ(у);

2) φ(αх)= α φ(х).

Опр: Пусть . Ненулевой в-ор х V наз-ся собственным вектором опер-ра φ, если существует λ Р, φ(х) = λ х, (1) , при этом λ – собственное значение опер-ра φ, соответствующее собственному в-ру х.

Опр: Множество всех собственных значений опер-ра φ наз-ся спектром этого оператора.

Пр1:M_n,δ_n, λ=0 являются все многочлены нулевой степени собственного вектора.

Пр3: На плоскости р/м опер-ор поворота на угол некратный π, такой опер-ор не будет иметь ни одного собственного в-ра.

Из опред.след., что если х – собственный в-ор опер-ра φ с собственное значением λ, то в-ор λх, тоже собственный в-ор с этим же собственным значением λ≠0.

φ(х)= λх

φ(αх)=α φ(х)=α(λх)= λ(αх), где α≠0, т.е. любой собственный в-ор, порождает целое подпространство собственных в-ов (оно одномерно и нет нулевого в-ра), поэтому, в отношение собственных в-ов понятие «различные» некорректно, поэтому, интереснее р/м вопрос о линейной независимости собственных в-ов.

Т!!!: Собственные в-ры x₁,…,x_k опер-ра , соответ-щие различным собственным значениям λ₁≠ λ₂≠ …≠ λ_к, линейно независимы.

Док-во: Метод мат инд по k.

1. при k =1теорема выполняется, т.к. в-ор х₁ ненулевой.

2. Предположим, что это выполняется для системы из k-1 в-ов. Док-м, для k в-ов. Составим линейную комбинацию х₁,…х_к с некоторыми числами:

α₁х₁ + α₂х₂+…+ α_к-1х_к-1+ α_кх_к=0 (2)

Подействуем оператором φ на обе части последнего равенства:

λ₁α₁х₁ + λ₂α₂х₂+…+ λ_к-1α_к-1х_к-1+ λ_кα_кх_к=0(3)

Умножим (2) на λ_к и вычтем из него (3).

α₁(λ_к- λ₁)х₁ + α₂(λ_к- λ₂)х₂+…+α_к-1(λ_к- λ_к-1)х_к-1=0. Т.к. х₁,…,х_к-1 линейно-независимы, то по индуктивному предположению α₁=…= α_к-1=0. Подст.в(2).

α_к(х_к)=0, х_к≠0, тогда, α_к=0, векторы х₁,…,х_к линейно-независимы.

След: Линейный оператор, действующий в простр-е V размерности n может иметь не более n различных собственных значений.

Собственные значения матрицы лин.опер. находятся из харак.многочлена.

Харак. Многочленом матрицы А Р^nxn наз. ф-ия f(λ)=det(A- λE), λ Р.

Харак. многоч. лин.оператора φ наз. ф-ия f(λ)=det( φ- λε ) , ε- тождественный оператор.

Существование собств. в-ов лин.оператора.

Теорема!:Пусть V-лин. прост-во над полем P, число λ Р явл-ся собст. значением когда λ явл-ся корнем хар.многочл.опер-ра φ.

Уравнение Det ( φ- λε )=0-характерист-ое ур-ие оператора φ.

Чтобы найти собств.в-ра и собств значен-ия нужно:

1.построить хар-й мног-н опер-ра и найти его корни.

2.для каждого найденного собств.знач. λ₀ найти ненулевые в-ры ядра опер-ра ker(φ- λ₀ε ):

(φ-λ₀ε)(х) =0;(A- λ₀E)(х) =0;det| A- λ₀E |=0

Соб.вектора образуют лин. пространство.