4 Симплексный метод решения злп

Симплексный метод является методом решения задач линейного программирования. Задача линейного программирования заключается в изучении способов поиска наибольшего или наименьшего значений линейной функции при наличии линейных ограничений. Функция, наибольшее или наименьшее значение которой отыскивается, называется целевой функцией. Совокупность значений переменных, при которых достигается наибольшее или наименьшее значение, называется оптимальным планом. Всякая другая совокупность значений, удовлетворяющая ограничениям, определяет решение (допустимый план). Изменением знака целевой функции задача максимизации сводится к задаче минимизации и наоборот.

Система ограничений в данных задачах задается системой линейных уравнений:

. (2.1.1)

Среди неотрицательных решений системы надо найти такие, которые максимизировали бы линейную функцию

(2.1.2)

Если ограничительные условия заданы неравенствами, то их можно преобразовать в равенство путем введения новых неотрицательных переменных, так называемых балансовых (выравнивающих).

Например, в неравенстве достаточно добавить к левой части некоторую величину , и получится равенство .

Переменные x1, x2, … , xr называются базисными, где r – ранг матрицы, а весь набор { } называется базисом. Остальные переменные называются свободными. Выразим переменные x1, x2, … , xr через свободные переменные из системы (2.1.1):

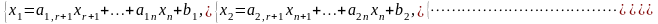(2.1.3)

Система (2.1.3) называется системой, приведенной к единичному базису.

Подставляя в линейную форму L (2.1.2) вместо базисных переменных их значения из системы (2.1.3), получим:

(2.1.4)

Полагаем, что все свободные переменные равны нулю. Тогда найдем значения базисных переменных .

Таким образом, решение является допустимым. Оно называется базисным: .

Решение задачи с помощью симплексного метода распадается на ряд шагов, заключающихся в том, что от данного базиса B мы переходим к другому базису с таким расчетом, чтобы значение уменьшалось (или увеличивалось для поиска максимума), т. е.

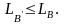
5 Оптимизация раскроя листовых и прутковых заготовок методом злп.

Листы материала размером 613 м нужно раскроить так, чтобы получить заготовки двух типов: 800 штук заготовок типа С (45 м) и 400 штук типа В (23 м), израсходовав при этом как можно меньше материала.

В математической постановке задача формулируется следующим образом. Обозначим через x_i число листов материала, раскраиваемых по i–му варианту и через сi , bi – число заготовок соответственно типа С и B при использовании i–го варианта раскроя. Параметры сi и bi представлены в табл. 6.1.1.

Таблица 6.1.1Варианты раскроя листовых заготовок

Тип заготовки	Варианты раскроя
	1	2	3	4
	Количество заготовок в варианте раскроя
С В	3 1	2 6	1 9	0 13

Необходимо найти минимум линейной функции, выражающей число израсходованных листов материала (по всем вариантам),

N(x1, x2, x3, x4)=x1+x2+x3+x4 , (6.1.1)

при условии, что переменные xi удовлетворяют следующим ограничениям:

(6.1.2)

Смысл данных ограничений в том, что соблюдена комплектность – все заготовки сделаны в достаточном числе. Подставляем в (6.1.2) сi и bi (см. табл. 6.1.1):

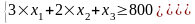(6.1.3)

Кроме того, необходимо ввести ограничения:

(6.1.4)

Ограничения означают, что ни один вариант не применяется к отрицательному числу материалов (т.е. из заготовок не будут изготовлены целые листы). Получим характерные условия задачи линейного программирования: найти минимум линейной функции при линейных ограничениях.

В прямоугольной системе координат XОY каждому возможному раскрою сопоставим точку, у которой координата X равна числу заготовок типа С, а координата Y – числу заготовок типа В. Эти точки обозначены буквой А с индексом, указывающим номер варианта раскроя. Например, первому варианту соответствует точка А1 с координатами x1 = 3, y1=1. Точка на отрезке А1А2 указывает своими координатами количество заготовок типа С и типа В, приходящихся в среднем на один лист материала в вариантах раскроя, которые представляют собой сочетания раскроев А1 и А2. Множество всевозможных планов раскроя, представляющих собой комбинации А1, А2, А3, А4, изображается совокупностью точек многоугольника ОА1А2А3А4.

Из всей совокупности возможных планов раскроя нас интересуют осуществимые планы, для которых выполнено условие комплектности. В них отношение числа заготовок типа С к числу заготовок типа В равно двум (800:400 = 2). Эти планы соответствуют точкам, лежащим на луче L2. Точка M1 принадлежит одновременно многоугольнику ОА1А2А3А4 и лучу L2 , поэтому соответствует плану, дающему наибольший выход заготовок в пропорции 2:1 на один лист. Следовательно оптимальный план раскроя расположен в точке M1 . Так как точка M1 находится на отрезке A1A2, то оптимальный план представляет собой комбинацию вариантов раскроя 1 и 2.

Обозначим через Z долю материала, которая кроится по варианту 1, остальная часть (1-Z) кроится по варианту 2. Из условия комплектности:

x1 Z+ x2 (1-Z) = 2 [y1 Z+ y2 (1-Z)] (6.1.5)

Подставляем значения x1, x2, y1, y2:

3 Z + 2 (1- Z ) = 2 [1 Z + 6 (1- Z)] ,(6.1.6)

откуда Z = .

Искомое минимальное число листов материала N находится из условия получения нужного числа заготовок типа С:

(6.1.7)

Решая уравнение (6.1.6), получаем необходимое (минимальное) число листов материала: Тогда

Следовательно, оптимальный план раскроя следующий: по варианту 1 кроятся 250 листов, а по варианту 2 – 25 листов.

Построение плана раскроя прутковых заготовок

Из прутка длиной 4000 мм необходимо получить комплекты заготовок, представленные в табл. 6.2.1.

Таблица 6.2.1 Комплект прутковых заготовок

Номер детали	Длина заготовок, мм	Количество заготовок на одно изделие
1	698	8
2	518	8

Варианты раскроя прутков длиной 4000 мм на заготовки представлены в табл. 6.2.2.

Таблица 6.2.2 Варианты раскроя исходных прутков

Вариант раскроя	Состав раскроя
А1	6985
А2	6984+5182
А3	6983+5183
А4	6982+5185
А5	6981+5186
А6	5187

Построим график. Координата x представляет собой число заготовок длиной 698 мм. Координата y – число заготовок длиной 518 мм. Условию комплектности (8 и 8) удовлетворяют планы лежащие на луче L1.

Точка М не может выйти за пределы области ОА1А2А4А6. Наиболее эффективным будет план в точке М1 , расположенной при пересечении луча L1 и отрезка А2А4. Чтобы получить такой план, надо использовать одновременно вариант А2 и А4. Обозначим Z долю материала, который нужно раскроить по варианту А4. Тогда доля материала раскраиваемого по варианту А2 равняется (1-Z). Должно соблюдаться условие комплектности (8 и 8):

x4 Z + x2 (1- Z)= y4 Z + y2 (1- Z) (6.2.1)

Подставляем значения x4, x2, y4, y2: 2 Z + 4(1- Z) = 5 Z + 2(1- Z).

Отсюда . Таким образом, оптимальным будет раскрой, при котором по варианту А4 надо раскроить необходимого материала, а по варианту А2 – .

Таблица 6.2.3 Комплект прутковых заготовок № 2

Номер детали	Длина заготовок, мм	Количество заготовок в изделии
1	698	3
2	518	1

Оптимальная точка М2 должна лежать на луче L2 , т. е. между вариантами раскроя А1 и А2. Оптимальный план раскроя должен включать в себя варианты А1 и А2. Так как по условию комплектности на три детали 1 требуется одна деталь 2, получаем уравнение:

x1 Z + x2 (1- Z) = 3 [y1 Z + y2 (1- Z)] . (6.2.2)

Подставляем значения x1, x2, y1, y2:

5 Z + 4 (1- Z) = 3 [0 Z + 2 (1- Z)], (6.2.3)

отсюда .

Таким образом, по варианту А1 надо раскроить объема заготовок, а по варианту А2 – .