Что нужно знать для составления общих решений уравнения

1) Уметь составить характеристическое уравнение по виду дифференциального уравнения. Для этого нужно формально заменить любой буквой в степени n: заменить , заменить , заменить .

2) Уметь решать квадратное уравнение по формуле

или по теореме Виета .

3) Знать на память вид общего решения в зависимости .

5. Решение неоднородного линейного дифференциального уравнения второго порядка с постоянными коэффициентами основывается на следующей теореме.

Теорема. Если  некоторое частное решение неоднородного уравнения и  общее решение соответствующего однородного уравнения , то общее решение неоднородного уравнения имеет вид .

Правило нахождения частного решения неоднородного уравнения методом неопределенных коэффициентов.

1. Пусть , где  многочлен степени n, тогда:

а) , где  многочлен той же степени n с неопределенными коэффициентами, если и ;

б) , если (или );

в) , если .

2. Пусть , тогда:

а) , если ;

б) , если (или );

в) , если .

3. Пусть , где и  многочлены, наибольшая степень которых n, тогда:

а) , если ;

б) , если , где и  многочлены с неопределенными коэффициентами.

Пример 1. Найти общее решение уравнения .

▲ Так как функции и  однородные второго измерения, то данное уравнение – однородное (см. п. 2). Сделаем замену . Тогда

.

Предполагая, что , сокращаем обе части уравнения . Далее имеем:

.

Разделяя переменные (для разделения переменных необходимо перенести все, что содержит t в одну сторону, а все, что содержит x  в другую, при этом и должны быть только в числителях), последовательно находим:

.

В последнее выражение вместо переменной t подставим значение . Получим общий интеграл . Разрешив его относительно y, найдем общее решение исходного дифференциального уравнения: . ▼

Пример 2. Найти общее решение уравнения .

▲ 1. Убедившись, что данное уравнение линейное (см. п. 2), полагаем

, тогда

и данное уравнение преобразуется к виду

.

Составим систему для определения u и v:

Решаем первое уравнение системы (при определении v не нужно писать произвольную постоянную величину, ибо достаточно знать с точностью до постоянной величины). Подставляем во второе уравнение системы и решаем полученное уравнение:

.

Зная u и v, находим искомую функцию y: .

2. Перепишем данное уравнение так: . Рассмотрим однородное уравнение . Так как (значение не является решением неоднородного уравнения), то



общее решение однородного уравнения.

Применяем далее метод вариации произвольной постоянной C. Общее решение неоднородного уравнения будем искать в виде

.

Подставив значения y и в неоднородное уравнение, получим

.

Т.к. , то .

Подставив это значение в общее решение неоднородного уравнения, получим  общее решение неоднородного уравнения. ▼

Пример 3. Найти общее решение уравнения .

▲ В уравнении нет в явном виде искомой функции y. Понизим порядок этого уравнения, положив . Тогда и исходное уравнение превращается в уравнение с разделяющимися переменными

.

Т.к. , то последнее уравнение является дифференциальным уравнением с разделяющимися переменными

.

Получили общее решение исходного уравнения . ▼

Пример 4. Найти общее решение уравнения .

▲ В уравнении нет в явном виде аргумента x. Понизим порядок уравнения подстановкой , тогда и исходное уравнение превращается в уравнение с разделяющимися переменными

.

Т.к. , то последнее уравнение является дифференциальным уравнением 1-го порядка с разделяющимися переменными

. ▼

Пример 5. Найти общее решение уравнения и частное решение, удовлетворяющее начальным условиям , .

▲ Рассмотрим однородное уравнение . Соответствующее характеристическое уравнение имеет вид , откуда , . Следовательно,  общее решение однородного уравнения.

Подберем вид частного решения для данного уравнения.

Подставляя и в неоднородное исходное уравнение, получим тождество (  решение данного уравнения). Для удобства вычислений будем выписывать выражения , , в отдельные строки и слева за вертикальной чертой помещать коэффициенты, стоящие перед ними в уравнении. Умножая эти выражения на коэффициенты, складывая и приводя подобные члены, имеем:

.

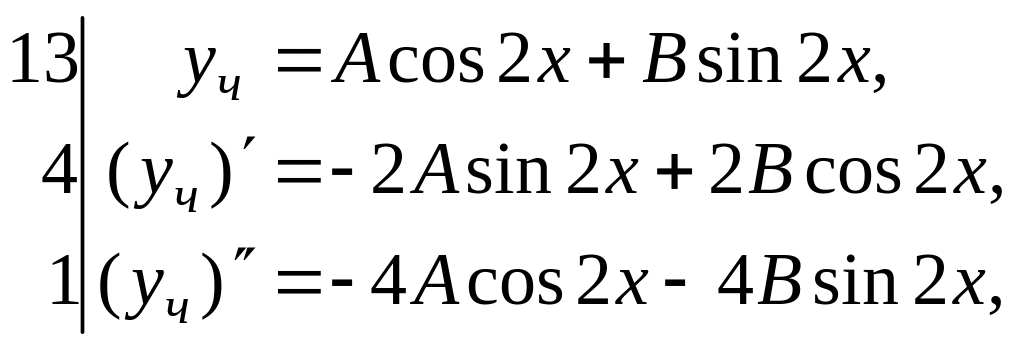
Приравнивая коэффициенты при подобных членах в левой и правой части последнего тождества, находим и :

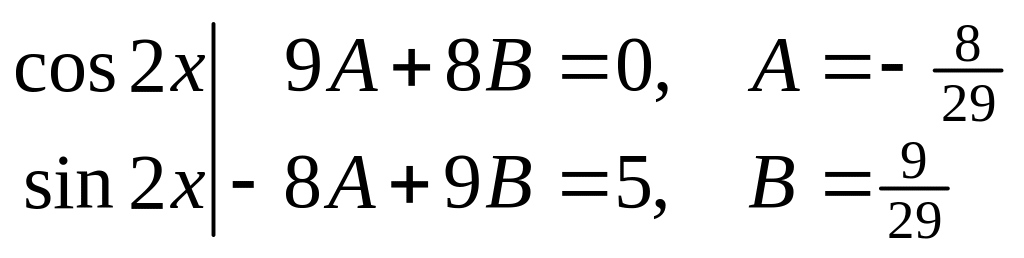
Итак, частное решение неоднородного уравнения имеет вид

,

а общее решение неоднородного уравнения 

.

Найдем частное решение, удовлетворяющее заданным начальным условиям:

Искомое частное решение таково:

. ▼